沉桩挤土效应对桩周土体径向位移数值分析

李家华,单恒年,陈 祥

(中交第四航务工程勘察设计院有限公司，广州 510230)

早在20世纪70年代，国内外学者就对沉桩挤土效应的研究做了大量的工作。归纳起来，可总结为以下几种方法：圆孔扩张理论、应变路径法、有限元分析法。目前对沉桩挤土效应的分析和解答大部分都是基于经典平面圆孔扩张理论[3]，在岩土工程领域中被广泛地运用于沉桩引起的应力、孔压和土体位移、原位测试(如旁压试验和静力触探)、爆破形成的弹坑等工程问题的分析中，另外常用的方法还有：应变路径法、试验方法、有限元数值模拟法等。沉桩过程桩土相互作用由于其涉及到几何非线性、接触非线性、材料非线性、大变形、本构模型等一系列的问题，仅仅凭借着理论公式的推导和试验研究不足以满足越来越精确的工程要求，以及实际施工过程中的复杂性。有限单元法(Finite Element Method)的出现，使有限元分析(Finite Element Analysis)成为了解决这些非线性复杂问题的一个有效途径[4]。采用ABAQUS有限元分析软件，首先建立合理的有限元模型，并与文献中的离心试验数据进行比较，证明模型的正确性和合理性，通过有限元模拟，研究沉桩过程中桩周土体的径向位移变化规律。

1 沉桩有限元分析模型构建

有限元模型土体的尺寸及参数参照离心试验来设置。假设桩径为0.3 m,桩长为5.0 m，桩靴角度为60°，桩靴采用光滑过渡。为了减小土体边界条件的影响，将土体的分析区域长度方向设为两倍桩长即10 m，宽度方向设为一倍桩长即5 m，同时为了防止土体挤压变形穿越轴线，要预留刚性小管间隙0.001 m。土体采用修正剑桥模型，模型近似尺寸设定为40，其他土体重要参数如表1所示。

表1 离心模型试验土体参数Tab.1 Soil parameters of centrifuge test data

根据已有条件建立模型，1/2轴对称有限元模型及网格划分情况，模型采用Abaqus/Standard中的大变形计算，将沉桩简化为平面轴对称问题，通过控制分析步对桩顶施加向下位移进行模拟沉桩，最后从后处理中导出模拟结果，如图1所示。

图1 桩土模型(轴对称1/2模型)Fig.1 Pile-soil model (axisymmetric 1/2 model)

1.1 土体本构模型

沉桩会使土体产生弹塑性区，即要考虑弹性区的本构模型也要考虑塑性区的本构模型。弹性部分，采用多孔介质弹性模型，它是一种非线性的各向同性弹性模型，可设置渗透系数，与孔压单元一起使用。塑性部分，采用临界状态塑性模型(修正剑桥模型)。它能与弹性部分多孔介质弹性模型很好的联合起来使用[5]，可以定义初始应力，求解孔隙水压力的变化。模型采用相关联流动法则，塑性势面与屈服面相同，如果初始应力状态点落在屈服面外侧，Abaqus会自动调整初始屈服面的位置。

1.2 荷载边界条件

在初始分析步ini(Gesostatic分析步)中设置Body Force(体力)为浮重度-9 kN/m3。对于单桩贯入的问题，桩的贯入通过桩顶参考点RP施加向下的位移来模拟，桩顶位移可在初始应力平衡后的后续分析步中施加，在初始分析步中，U1、U2及UR3均设置为0。另外，在土体中心线处的边界条件设置也需要特别注意。本模型简化为平面轴对称问题来求解，因此不能发生穿越中心线的情况发生，但是远离桩中心线可以发生挤土效应，简单起见，采用一个很实用的方法来解决这个问题：在桩的底部加上一个直径为1 mm的刚性小管，沿着小管的法线方向，不能承受拉力，可模拟土体开裂，阻止土体穿越中心线的位移产生。同时，还需要定义土体底面的水平和竖向位移均为0，定义土体右侧的水平位移为0，土体左侧的边界条件由接触条件来控制，无须设置，土体的边界条件在初始分析步ini中定义生效。

1.3 平衡初始应力

定义初始应力需要注意两个方面：首先是平衡条件，为了得到初始位移为0的状态，应力场形成的等效节点荷载要和外荷载相平衡；其次是屈服条件，初始应力场若通过高斯点的应力状态来施加，往往会出现一些高斯点的应力状态落在屈服面之外，虽然在后续的计算当中，超出屈服面的应力可以通过应力来调整，但毕竟是不正确的，需要消耗大量的迭代，甚至可能出现不收敛的情况。基于以上两方面条件，常用的平衡初始应力方法是[6]：首先将重力荷载施加于土体，并施加相应的实际工程荷载和边界条件，计算在重力载荷下的应力场，再将此应力场定义为初始应力场与原重力荷载一起施加在有限元模型上，这样就可以得到满足平衡条件且不违背屈服准则的初始应力场，保证各节点的初始位移接近为0。若地表是水平的，则可以极大的减少定义初始应力的工作量。

1.4 接触问题

由于接触面的不连续约束及力学模型本身的非线性，在数值模拟中常常会出现不收敛的情况。Abaqus采用的主-从面接触法，一个完整的接触模拟首先需要定义主控面(master surface)和从属面(slave surface)，然后再定义它们的接触状态，接触属性等。由于本模型绝大部分涉及到接触问题，不允许土体穿透中心线，所以采用点对面的离散法，更易收敛。

1.5 网格ALE技术

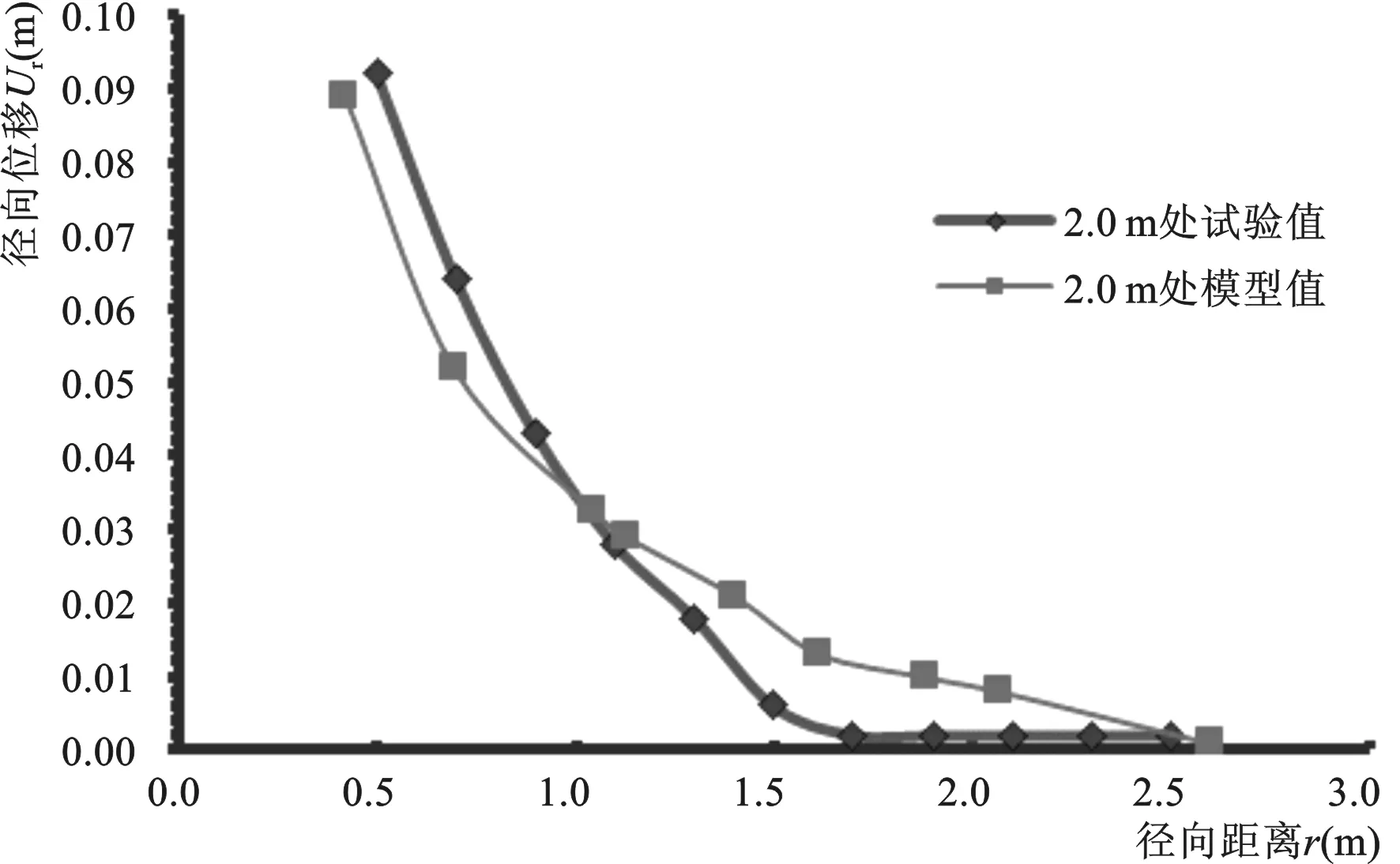
图2 深度2.0 m处桩侧土体水平位移试验值 与模型值比较图Fig.2 Comparison of horizontal displacement test value and model value of pile soil at depth 2.0 m

静压桩沉入的过程中，在桩尖及桩端处存在着大应变、大变形，网格将会扭曲的很明显，随着桩的沉入，边界条件也在不断的改变，位移的模式实际上是跳跃的，需要重新去确定边界问题，比较难收敛。在有限元软件Abaqus中，提供了一系列自适应的技术，如任意拉格朗日-欧拉法自适应网格划分技术(Arbitrary Lagrangian Eulerian adaptiove meshing)等用来处理高度扭曲的网格。ALE分析步可以分为两个步骤：(1)创建一个新的网格；(2)将旧网格的变量信息，其中包括应力场、应变场与动变量等，传输到新网格上。这样做可以使网格与物质相分离，即使发生了网格大变形，也能保证在分析计算中网格的高质量。ALE技术与原网格有一定的相关性，所以要保证初始网格才能提高ALE技术的效率。由于靠近中心线的土体区域是高应变区，网格的扭曲很严重，所以在分析步中设置ALE区域位于离轴线2 m的矩形区域，同时分别设置自适应技术里的频率控制与对数控制。频率控制(Frequency)主要是对每个分析步时间步长里网格的重划分次数控制，对于拉格朗日问题，默认参数为10，对欧拉问题，默认值为1，本模型选用1；参数控制(Mesh Sweeps)是对整个自适应重划分的每个子过程的控制，需要在新网格的基础上再进行sweep，本模型选用1。使用ALE技术会对输出结果带来一定的影响，在未使用ALE网格划分技术时，物质点与网格点在计算过程中是保持相互重合的，使用完之后，网格的节点的位移将不能表示物质点的位移状态变化，而是物质点移动与网格重划分共同影响的，也就是说节点处的位移将不代表物质点真实的位移，所有位移的云图变化将不再是准确的，而历史变量随时间的变化也都是无效的。

1.6 验证有限元模型

在有限元模型中对桩顶参考点施加向下的位移5 m，时间步设为500 s，近似模拟1 cm/s的沉桩速率，与离心模拟试验沉桩速率相符，由于设备有限，离心试验[2]只对土体位移和孔压进行了研究，完成后的模型数据与离心试验数据比较，2.0 m深处桩侧土体水平位移试验值与模型值分布如图2所示。

可以看出，模型值与试验值具有类似的分布规律，且误差在允许范围内，证明了有限元模型的合理性，可以借助该模型进行进一步的研究。

2 沉桩过程土体径向位移变化规律有限元分析

2.1 沉桩过程土体径向位移变化规律

利用有限元模型模拟沉桩过程，分析沉桩至不同深度时土体径向位移变化规律，如图3所示。

3-a 沉桩过程中土体表面径向位移变化3-b 沉桩过程径向距离r=2 d(d为桩直径)处深度方向径向位移变化图3 沉桩过程土体径向位移模型数值变化图Fig.3 Numerical simulation of soil radial displacement model during pile driving

由图3分析可知：(1)地表的土体被桩向外挤出，径向位移Ur且随径向距离r的增大呈对数衰减，且靠近桩的地方，挤土效应更加明显，衰减越快。随着桩体的沉入，土表面径向位移增加不大，保持对数衰减的趋势；(2)沿深度方向，径向位移有减小的趋势，但在桩端以上0.5～1.5 m处达到最大值。Jim-HungHwang[7]等人在1994年通过观测发现这个距离为10d，原因在于本文取的是均质土层，而实际土质并非是均匀的，并且在沉桩的过程中，土体也在不断的重组，位移也在发生着变化。

2.2 土体参数对土体径向位移影响

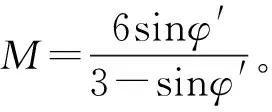
表2 沉桩过程不同参数下桩周土体径向位移值Tab.2 Radial displacement of soil around pile in different parameters of pile driving process m

整埋数据，可得到沉桩过程桩周土体的径向位移变化规律，如图4。

4-a 泊松比υ对径向位移的影响 4-b 试验参数λ对径向位移的影响

4-c 试验参数κ对径向位移的影响 4-d 有效内摩擦角φ′对径向位移的影响图4 沉桩过程不同土体参数下桩周土体径向位移值变化规律Fig.4 Variation law of radial displacement of soil around the pile under different soil parameters during the process of pile driving

分析可得：(1)在距离桩入土较近的区域，土体径向位移受泊松比影响不大，但是随着径向距离的增大，泊松比开始影响土体的径向位移，泊松比越大，径向位移也越大；(2)试验参数λ、κ是剑桥模型中各向等压加荷曲线和卸荷曲线的斜率，当λ增大时，径向位移以一定的幅度增大，当κ增大时，则径向位移相对减小，远离桩向的土体径向位移基本不受影响；(3)有效内摩擦角φ′在修正剑桥模型中存在的形式较为复杂，所以影响规律也不是单调的增加或减少，在径向距离较小时有效内摩擦角的改变影响不大，在0.4～0.8 m的范围内，有效内摩擦角的增大，径向位移相应减小，而在0.8 m以外有效内摩擦角增大，径向位移相应增大。

3 结语

关于桩的挤土效应的研究一直以来都是学者们关注的焦点，从理论推导到试验研究再到现在的数值模拟，仍处在不断的发展中。关于沉桩挤土效应机理的研究更是因其特殊性而成为桩土相互作用研究的重中之重，结合离心模拟试验的结果，利用Abaqus有限元分析软件建立沉桩模型，将模型计算得到径向位移值与试验检测出来的水平位移值进行比较，验证模型的合理性，同时对沉桩过程桩侧土体的变形特性进行分析，为施工设计提供借鉴，具有很大的理论意义和实际意义。本文将沉桩简化为平面轴对称问题，利用Abaqus有限元软件建立沉桩模型，通过控制分析步对桩顶施加向下位移进行模拟，最后从后处理中导出模拟结果。沉桩过程中，桩周土体被挤开，径向位移比较大的区域主要集中在桩附近，并随着与桩中心距离增加而对数衰减，到一定范围之后则没有什么影响。在沿沉桩的深度方向，径向位移并不是线性增大，而是在桩底以上一定距离处达到最大值，这主要是受到土体重组的影响。另外，本文也研究了土质参数对沉桩时土体径向位移的影响，它与有限元模型中所采用的土体模型密切相关，在不同区域范围里，具有各自变化的规律，其中，泊松比系数在径向距离大于1 m时才开始显著影响径向位移的大小；试验参数λ增大时，土体径向位移也随之增大；试验参数κ则相反；有效内摩擦角φ′对土体径向位移的影响规律较为复杂，在0.4～0.8 m的范围内，有效内摩擦角的增大，径向位移相应减小，而在0.8 m以外有效内摩擦角增大，径向位移相应增大。