基于短时交通流预测的单交叉口自适应控制
2018-09-20徐建闽李岿林翟春杰肖雅惠
徐建闽,李岿林,翟春杰,肖雅惠
(1. 华南理工大学 自动化科学与工程学院,广东 广州 510640; 2. 华南理工大学 土木与交通学院,广东 广州 510640)
0 引 言
城市单个交叉路口是智能交通系统的最小控制单元,随着城市路网密度的增大,交叉口之间的相关性日益明显,多交叉路口间的协调控制改善了路网的通行效率。然而,依然存在较多的交叉口无法与邻近的交叉口进行协调控制[1]。因此,优化单交叉口信号控制对提高城市道路的通行效率具有重要的意义[2]。当前,对单交叉口的控制方法主要分为:定时控制、感应控制和自适应控制[3-15]。其中,定时控制又分为固定定时和分段定时控制,固定定时指以固定不变的配时方案来控制交叉口,分段定时指在高峰和平峰时段切换不同的配时方案,此外,定时控制都是基于历史数据得到的配时方案,不适用于一些交通流量变化大的情况[4]。感应控制分为半感应控制和全感应控制[5],半感应控制是以主干道优先通行为原则,主要适用于支路交通流量非常少的情况;全感应控制以车来即延时为原则,根据经验设定相关参数,主要适用于交通流量随机波动大且流量较小的情况。自适应控制是将单交叉路口看作不确定的系统,将实时检测的交通状态信息作为输入参数的值[6-8],经过计算得到输出参数的值,进而使控制系统达到最优状态,弥补了前两种控制方式的不足[16]。
目前,对单交叉口自适应控制可分为方案选择自适应控制和模型优化计算自适应控制[9]。方案选择自适应控制是根据可能的多种交通流,预先设计好方案存储在计算机内,在执行过程中根据实时采集的参数信息进行方案选择[10],这实际上还是基于模糊逻辑的半自适应的控制;模型优化计算自适应控制核心是在线生成控制方案,显然自适应程度更高。然而,一般自适应反馈控制本身是一种滞后控制,即当前控制信息是基于上一时段的交通状态信息反馈而得到的,控制效果滞后;其次,对于模型优化计算自适应控制,如果模型复杂,计算量大,对硬件要求很高,影响执行效率。因此,交通流参数获取的滞后性和建立较为简化的自适应控制模型可以显著地改善自适应方法的控制效果。
针对上述自适应控制的问题,引入短时交通流预测机制,建立简化计算的自适应模型,主要内容是:首先根据单交叉路口的历史流量,采用K近邻算法[11-13]实时预测未来5 min的交通流量,计算最大的信号周期;然后建立自适应控制模型,实时更新每个周期的相位时间和相序;最后结合广州市南沙区某交叉口数据,通过Vissim4.3仿真软件对自适应控制模型进行验证。
1 短时预测方法
1.1 预测步骤
交通流量的变化具有一定的规律性和随机性,规律性体现在工作日的流量早高峰、平峰和晚高峰的波动情况,使得交通流量具有可预测性;随机性体现在每天相同时刻的交通流量可能不相同,这给预测带来了不确定性。利用预测的流量数据计算周期,预测方法不宜太复杂,允许有一定的偏差。采用文献[11]提出的基于数据驱动的K近邻非参数回归模型对交叉口的直行和左转方向的交通流量进行短时预测,预测时间间隔为5 min,预测流程如图1。

图1 K近邻预测算法流程Fig. 1 K-nearest neighbor prediction algorithm process
预测主要步骤:
1)建立历史流量数据库:对一个月的历史流量数据分为工作日和非工作日两类[14],并且进行数据过滤,每天以5 min间隔存储;
2)状态向量构造:状态向量只考虑交通流量这一个参数,构造状态向量[Vi(t-3),Vi(t-2),Vi(t-1)],其中Vi(t-n)表示当前时刻的前面第n个时刻。构造状态向量的作用在于:如果某断面连续3个时间段的交通流量都与历史数据中某一组数据相临近,则这组历史数据可以作为当前时刻的一个近邻。
3)选择合适的近邻个数:依据历史流量数据库的大小,笔者只有1个月的交通流量数据,故选取所有能够匹配的数据作为近邻。
4)预测算法:为了简化计算,提高效率,对于每一个近邻不分时间的远近,采用等权重法求平均值,即:
(1)
式中:V(t)为t时间段的预测值;Vi(t)为t时间段的近邻历史值;K为搜索到的近邻个数。
1.2 预测算法验证
以广州市南沙区环市大道-市南大道交叉口(以下简称环市交叉路口)东进直行道路为例,数据来自道路上面的地磁线圈检测器,检测时间间隔为5 min,取2015年11月份每天15:00—21:00的数据,对11月30 日的断面交通流量进行预测,将预测值与实际值对比,如图2。预测结果表明,预测流量和实际流量偏差在合理的范围内,因此,运用K近邻方法预测交叉口交通流量是可行的。

图2 交通流量预测结果Fig. 2 Traffic flow prediction results
2 单交叉口自适应控制模型
2.1 城市交叉口说明
根据交通流理论,右转车流在任何时刻都不与其他车流冲突,因此对于交叉口只要控制直行和左转车流的通行即可,不考虑行人因素。不冲突的车流组成一个相位,如图3,是一个东西左转、东西直行、南北左转、南北直行等4个相位的组合,分别记作相位P1,P2,P3和P4,笔者的自适应控制方案是基于图3中的4种相位集合。

图3 交叉口相位示意Fig. 3 Intersection phase diagram
道路交叉口的几何条件如图4,是一个双向8车道的对称交叉口,右转车道宽度为3.5 m,其余车道宽度为3 m,限速50 km/h;在每条左转和直行车道上,布置两个地磁线圈检测器D(in)和D(out),定义两个检测器之间的路段为滞留区,滞留区的长度要根据交叉口实际的最大排队车辆数来确定,笔者设置为100 m,图中标示以西进直行车道为例。
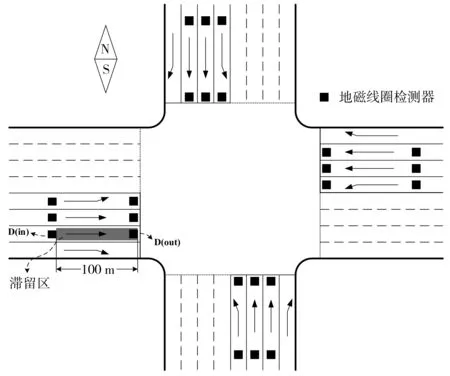
图4 交叉口几何条件Fig. 4 Geometric conditions of intersection
2.2 车辆检测方法
滞留区车辆检测方法为:假设在同一车道上同时读取通过D(in)的车辆数为qin,通过D(out)的车辆数为qout,则该车道滞留区车辆数Δq=qin-qout,事实上,滞留区的车辆数量就可以等效为排队车辆数。
为了减小滞留区车辆数量检测偏差,考虑车辆在滞留区变换车道的情况,将情况分为两种:
1)车辆在两条直行车道之间变换。由于两条直行车道车流属于同一相位,因此将直行车道上的两个D(in)检测器联接为一个,此时Δq=qin-qout1-qout2,其中qout1和qout2分别为两条直行车道D(out)检测器的车辆计数,Δq为本相位直行车道滞留区数量。
2)车辆在直行与左转车道之间变换。可以适当的延长直行和左转车道分界线实线的长度,并定时清空车辆检测器数值,避免偏差积累。
2.3 模型建立
目前交通流理论研究了交通流符合某种概率分布的特性,在宏观的交通控制中发挥了重要的作用。然而,对于单点交叉口控制来说,交通流本身随机性较大,某一确定的周期、相序和相位时间等参数无法始终做到对交叉口进行最优控制。笔者的自适应控制策略根据实时的滞留区车辆数量,计算出每一信号周期的相序和最大相位时间,并且根据流量预测值,每隔5 min计算信号周期,做到灵活地适应交叉口流量的变化。设定每个周期左转和直行交通流均有一次通行权,且相位时间至少等于最小绿灯时间。模型主要分为3个方面:周期计算、最大相位时间计算和相序确定。
1)周期计算
常用的交叉口最佳周期计算方法主要有Webster法[17],该方法计算以车辆延误时间最小为目标计算得到最佳信号周期,但是只适用于流量饱和度不高的情况,因此,在饱和度较高时,模型采用文献[17]基于美国HCM2000改进的估算公式计算周期。
Webster公式:
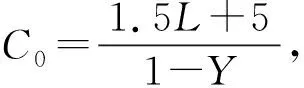
(2)
HCM2000改进估算公式:
C0=1.23Le(2.46-0.02L)Y,若Y≥0.6
(3)
式中:C0为最佳信号周期时间;L为每个周期总的损失时间;Y为每个相位关键流量比之和。
2)最大相位时间计算
Pa∪Pw={P1,P2,P3,P4}
(4)
(5)
tp_min=tg_min+tyellow
(6)
(7)
(8)

3)相序确定
根据式(9),确定下一执行相位,主要分为以下两种情况:
Qw=max{Qi,Qj,Qm,Qn}
(9)
满足i,j,m,n∈Pw且i≠j≠m≠n。
式中:Qw为在一个周期内未执行相位滞留车辆数量最大的相位集合。
情况1:如果集合Qw元素个数唯一,则下一执行相位为第w相位;
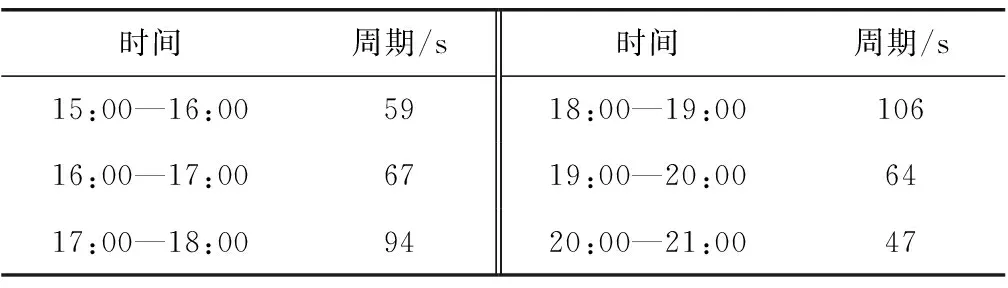
情况2:如果集合Qw元素个数不唯一,那么至少存在两个相等的最大值,假设为Qw={Qm,Qn}且m 设定tg_min=10 s,tyellow=3 s ,tdelay=2 s ,定义CN和CW分别为当前5 min内的周期和下一个5 min内的周期,ti为第i相位执行时间计数器,Count为全局仿真时间计数器,自适应控制流程如下: Step1:初始化。当前周期C0=CN,执行Step 3; Step2:预测下一个5 min内的流量。运用式(2)和式(3)求得在未来5 min的信号周期C0=CW; Step5:判断是否结束绿灯延时。在tdelay的最后1 s读取第i相位车道上D(out)检测器的状态,判断是否有车辆在路口排队,如果有则执行Step4; Step6:第i相位绿灯结束。进入黄灯,时间为tyellow,黄灯结束后,如果本周期未执行相位集合Pw≠Ø,则执行Step 3; 以环市交叉路口为仿真对象,利用交通仿真软件Vissim4.3进行仿真,如图5。分别对固定定时、分段定时和自适应控制3种方式在相同条件下进行仿真,其中分段定时和自适应控制的仿真采用VS C#2010调用VISSIM提供的COM接口实现。仿真时间为6 h,即21 600个仿真步长。3种控制方法利用式(2)和式(3)计算周期,其中固定定时以仿真期间总的平均流量计算得到最优周期为86 s;分段定时以每小时平均流量计算周期,各时段最优信号周期如表1,能够适应每小时变化的流量;自适应控制以每5 min预测的流量计算一次最大周期,依据自适应控制流程进行仿真。 图5 实例仿真几何图Fig. 5 Simulation geometric diagram of the sample intersection 时间周期/s时间周期/s15:00—16:005918:00—19:0010616:00—17:006719:00—20:006417:00—18:009420:00—21:0047 以环市交叉路口数据为例,取2015年11月1日至2015年11月29日每天15:00—21:00各道路流量数据建立历史数据库;历史数据来自道路地磁线圈检测器,时间间隔为5 min,预测2015年11月30日各道路从15:00—21:00的流量数据。仿真路网输入流量为2015年11月30日从15:00—21:00每小时的流量,各个进口流量数据见表2。 表2 仿真交通流量分布Table 2 Traffic flow distribution in the simulation 根据对各相位交通流量的短时预测,计算出每隔5 min的最大信号周期,如图6,从周期变化的情况可以看出:在未饱和状态下,单交叉口每个短时段的最佳周期基本不同,相邻时段周期相差较大的情况较多。因此通过短时预测的方法提取短时片刻的车流量的变化状态加以反馈,实现最大信号周期持续性的微调,从而能够极大改善单交叉口自适应控制的控制效果。 图6 自适应短时信号周期序列Fig. 6 Self-adaptive short-time signal cycle sequence 仿真结果以所有相位车道上的车辆平均延误为评价指标,评价数据采集时间间隔为30 min,将定时控制、分段定时控制和自适应控制相比较,结果如表3。 表3 3种控制方式车辆平均延误时间对比Table 3 Comparison of average vehicle delays in three control methods 由表3可知,无论是高峰还是平峰时段,自适应控制方法与固定定时和分段定时方法相比,车辆平均延误均更小,比固定定时和分段定时总的平均延误分别减少35%和15%,因此,笔者所提出的方法能够有效的提高单交叉口的通行效率。 自适应控制方法通过地磁线圈实时获得车道滞留区的车辆数量,确定下一个执行的相位及其最大相位时间;在执行过程中,能够根据当前交通状况灵活地切换到下一个相位,充分适应随机变化的交通流,并且模型简单,易于实现。同时,运用数据驱动的非参数回归算法预测短时交通流量,能够对交叉口的交通状态趋势进行有效预测并计算未来短时段的最大信号周期,克服了传统自适应控制的滞后性。仿真结果表明,笔者提出的自适应控制比定时控制、分段定时控制方式下的车辆平均延误更少,显著的改善了单交叉口车辆的通行状况。2.4 自适应控制流程
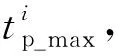


3 仿真与结果分析
3.1 方案设计

3.2 数据说明
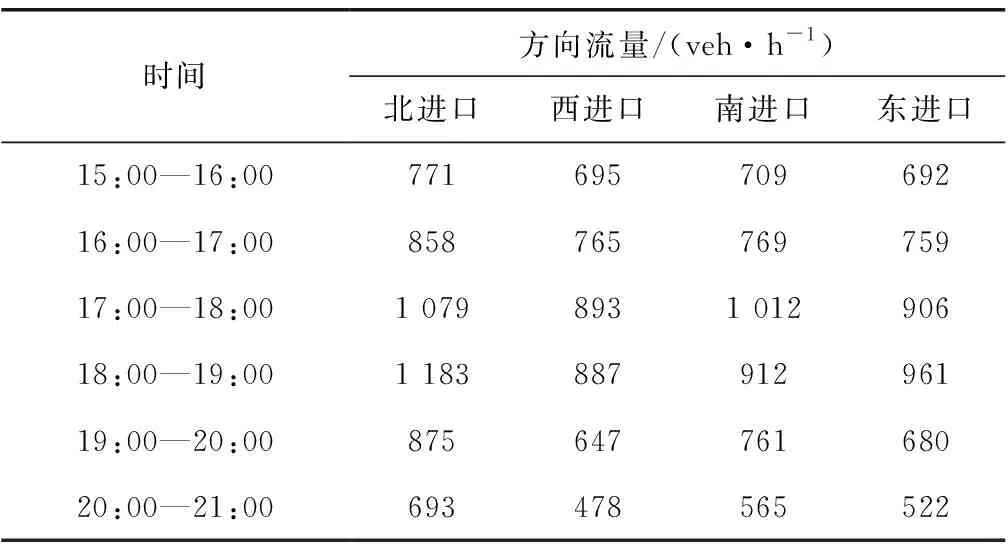
3.3 仿真结果


4 结 语
