基于多元回归-ARIMA-卡尔曼组合模型的风电功率超短期预测

文 | 刘震，刘丹，王彦文，孙书贝，刘冰

随着风电并网规模的快速扩大，风电的不确定性对电力系统与电力市场的稳定性、充裕性及经济学的影响也日益增大，故及时和准确地预测风电 功率（Wind Power，WP）的 意义重大。风电功率预测（Wind Power Prediction，WPP）根据风速及相关因素的历史数据，演化其后续的过程。具体需要建立数学模型来反映WP与相关因素的关系，外推WP值。WPP可按时间尺度分为中长期、短期和超短期预测。用于风电场规划及年度发电计划的长期预测以年为时效；用于检修计划的中期预测以周或月为时效。中长期预测对精度的要求不严格，但需要长时间的历史数据积累。短期预测则要求较高的精度，以减少弃风，优化常规电源的日发电计划与冷热备用，以及调整检修计划。超短期预测则有助于优化调频及旋转备用容量，以及在线优化机组组合与经济负荷调度。本文主要关注超短期预测。

超短期预测方法可以分为物理方法和统计方法。已有研究表明，对于超短期风电功率预测方法应采用统计方法。超短期风电功率预测中所用到统计预测方法有支持向量机、卡尔曼滤波法、自回归滑动平均（Auto Regressive Integrated Moving Average，ARIMA）模型、回归模型，人工神经网络（ANN）等人工智能算法。

超短期预测考核第4h点已是一种趋势，以上所提到的单体算法均不能很好拟合超短期第4h点的状态。基于此，本文提出组合算法进行超短期预测的研究。目前对组合算法的研究甚少，一般的研究思路是先对原始序列信号进行分解，再利用一些方法对子序列进行分类，最后对不同的子序列分别预测，再将预测值合并。所以说，此类组合方法体现在预测的不同阶段选取不同的算法进行处理，但原始序列相对单一，从而所携带的信息量也相对较少。本文是从影响目标各因素的角度出发，考虑了天气预报的影响，考虑了序列趋势和规律性的影响，考虑了系统预测误差的影响；选取了多元回归算法、自回归滑动平均（ARIMA）模型和卡尔曼滤波算法。本文将对这3种算法分别做独立的预测工作，得到3组预测结果，并给出3组预测结果的评价指标；最终将3种算法所得预测结果通过最小方差法做加权组合，得到一组新的预测结果，并给出相应的评价指标。

单体算法原理

一、多元回归算法原理

回归分析是预测最常用的方法之一。在实际工作中，某种现象或结果的产生通常与某些因素有关，我们通过数据分析可以看出其中存在的某种趋势和规律。

假设存在一个因变量y，n个自变量 （x1，x2， ，xn），则可建立它们之间的回归方程：

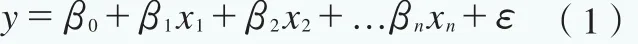
其中β0，β1，β2， ，βn为待定系数B，称为回归系数。若实验测得m组相互独立的数据，假设每次观测时的随机误差ε为白噪声，即ε～N（0，σ2）。为了求解系数B，则可利用最小二乘法来计算回归系数，使得残差平方和达到最小，求得待定系数为：

二、ARIMA方法原理

时间序列分析的主要目的是根据已有的历史数据对未来进行预测，时间序列中的时间可以是年份、季度、月份或其他任何时间形式；其次，其预测时效一般不会太长，且随着预报时长的增加，预测精度逐渐下降。时间序列模型主要包括稳定模型和非稳定模型。常用的稳定模型有自回归（Auto Regressive，AR）模型、滑动平均（Moving Average，MA）模型、自回归滑动平均（ARIMA）模型几种。非稳定模型可以经过差分或相应变换处理，将其转换成平稳序列，然后再使用上述常用的时间序列模型；一般对于非平稳序列比较常用的有差分自回归滑动平均（ARIMA）模型等。其中，ARIMA（p，d，q）模型的表达式为：

式中，｛Xt｝（t＝1，2，3， ）为时间序列；｛εt｝是均值为0、方差为σ2的白噪声过程；ϕi（i＝1，2， ，p）和θi（i＝1，2， ，q）为模型的系数；B为滞后算子；k＝1－B；ϕ（B）＝1－ϕ1B－ϕ2B2－ －ϕpBp；θ（B）＝ 1 －θ1B－θ2B2－ －θqBq。

在模型建立时，首先，根据训练数据的自相关系数ρk和偏相关系数ϕkk进行模型定阶；同时，选取最小信息准 则（Akaike Information Criterion，AIC）和BIC进行模型定阶，确定出p，q。通过训练数据得出模型系数估计值，得出模型表达式。

三、卡尔曼方法原理

卡尔曼于1960年提出卡尔曼滤波算法，后来，此算法在许多领域得到广泛的应用。卡尔曼滤波的本质是通过观测值重新构建了系统状态变量；通过以预测－观测－修正的流程依次迭代实现。所以，卡尔曼算法是一种动态修正的算法。

在卡尔曼滤波算法中，分为状态方程和测量方程，其数学表达式如下：

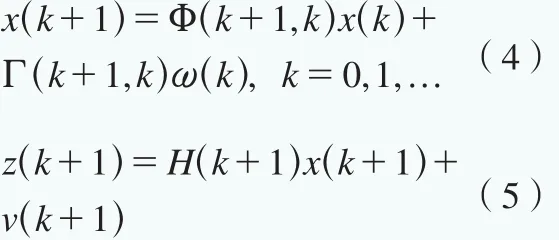
式中，x（k）为在k时刻的状态向量；z（k）为k时刻的观测向量；Φ（k＋1，k）和H（k＋1）分别为系统状态转移矩阵和输出转移矩阵；Γ（k＋1，k）为激励转移矩阵；ω（k）和v（k）分别为系统噪声以及测量噪声，假定为相互独立且服从高斯分布的白噪声；对应的协方差矩阵为W（k）和V（k）。

假设给定初始状态向量x（0）＝［0］，则是由下面的递推公式决定的，即：

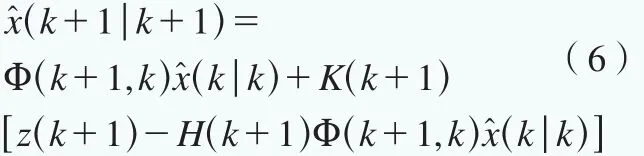
式中，K（k＋1）为卡尔曼增益（Kalman Gain），其计算公式如下：

为了使滤波器不断更新下去，还要更新k＋1时刻下状态x（k＋1）的协方差：

组合算法原理

组合预测方法的基本思想是将不同的预测方法结合起来，组合预测方法能够利用每个单体预测方法的信息；组合预测方法一般能增加系统预测的准确性和稳定性。

本文选取了三种单体算法，分别为多元回归算法、时间序列算法以及卡尔曼滤波算法，考虑因变量和自变量之间影响因素，选择了多元回归算法；从预测的时效性考虑选用了时间序列算法（ARIMA）；从动态修正的思想和系统误差的角度考虑使用了卡尔曼滤波算法。

目前常用的组合预测方法包括最小方差法、无约束（约束）最小二乘方法、Bayes方法等。在实际应用和理论研究中使用最多的是最小方差法，一般采用绝对误差作为准则来计算组合预测方法的权重系数。

假设第i个单体模型的误差为ei，方差为Var（ei）；组合预测模型的误差为e，方差为Var（e），则：

组合预测的方差可以写成：

要使得Var（e）达到最小，可以转化为如下优化问题来求解：

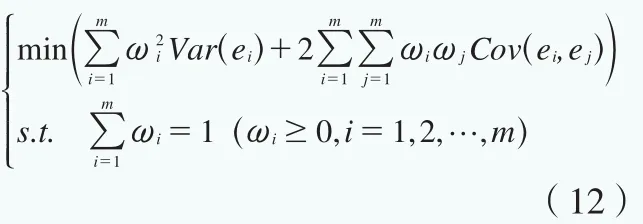
对这类约束优化问题一般采用拉格朗日乘数法来求解，最终得出：

可以证明Var（e）min≤min（Var（ei）），所以说，一般组合预测方法的效果会优于每种单体算法的效果。

实例分析

本文以中国云南省某8个风电场2016年的实际运行数据为例，数据主要包括实际功率和短期预测功率；实际功率数据是指现场实时的出力；短期预测功率数据由功率预测厂家提供；每种数据的分辨率均为15min，一天有96条记录。

一、评价指标的选取

根据国家能源局2011年对现行风电场风电功率预测预报的管理规定：风电实时预测（超短期预测）考核指标一般仅采用准确率指标，实时预测一般只是指未来15min～4h的预测。

（1）均方根误差RMSE：

（2）准确率r1：

式中，r1为预测计划曲线准确率；PMk为k时段的实际平均功率；PPk为k时段的预测平均功率；N为日考核总时段数（取96点－免考核点数）；Cap为风电场开机容量。

月（年）平均风电预测计划曲线准确率（%）为日平均预测计划曲线准确率的算术平均值。

二、结果分析

（一）各单体算法训练样本量的选取

本文将采用的3种单体算法分别进行研究，首先对其最优训练样本量进行选择和测试。测试训练样本量的选取从4h训练数据至40h训练数据，时间跨度为4h。分别对未来15min、1h、2h、3h以及4h时刻（分别对应第一个、第二个、第三个、第四个以及第五个点）的预测数据进行分析。以卡尔曼算法为例，图1为卡尔曼算法五个点的预测均方根误差与训练样本量之间的关系。

由图1可以看出，第一个点和第二个点的均方根误差随着训练样本量的增加，基本上是逐渐增大的；而到第三个点时，此规律就没有这么明显；第四和第五个点的均方根误差随着训练样本量的增加，几乎没有明显变化，呈现出相对稳定的状态。因为卡尔曼算法的原理就是修正系统误差，所以对邻近时刻的数据比较敏感。综合稳定性和各单体算法的原理，将3种单体算法的训练样本量设定为32（8h）个数据点。

（二）各单体算法的实现与验证

本文选取的自变量为短期预测功率和时间向前推4h历史实际功率，因变量为当前历史实际功率。同时，对回归模型残差服从标准正态分布的这一假设进行了验证。图2是多元回归残差的分布图，从图中可以看出残差基本是以0为中心，向左右两边均匀分布的。

图1 卡尔曼算法预测结果（不同预测点）的误差和训练样本量之间的关系

图2 多元回归模型所得残差频数分布直方图

图3 多元回归模型所得预测结果和实际功率曲线图

图3展示了回归模型的预测效果，可以看出，回归模型的预测在整体上是把握了整体趋势的变化；但在局部点上还是存在较大的差异。风电功率预测误差主要分为两种，第一种是纵向误差，第二种为横向误差；其中纵向误差主要描述了某一时段的预测结果在竖直方向与实际结果的差别，可以用偏大或偏小来衡量；而横向误差则主要描述预测结果在水平时间轴上与实际结果的差别。可见回归模型的优点就是降低了横向误差，但对纵向误差并没有明显的效果。

图4为训练数据经过平稳化后的ACF和PACF图，从图中可以看出，ACF和PACF都是1阶截尾的，所以可以初步确定模型为ARMA（1，1）。

最后，对未来4h的实际出力进行预测。图5是ARIMA算法所得的超短期预测结果和实际出力的对比图，可以看出，该模型能够降低预测功率和实际功率的纵向误差，较好地拟合未来4h实际功率的纵向波动。

卡尔曼算法主要从动态修正的思想和系统误差这一方向来解决问题。卡尔曼算法的输入数据为历史实际功率和短期预测功率，通过实时数据动态修正短期预测功率。图6展示了卡尔曼算法的修正效果，从图中可以看出，经过卡尔曼算法对误差的动态修正，使得超短期的预测更能“贴近”实际功率。因此，与多元回归模型不同的是卡尔曼算法对降低纵向误差有着显著的效果。

（三）组合算法的实现与验证

通过对每个单体算法的分析与验证，给出了本文选取此3种算法的依据。将这3种算法通过最小方差组合算法进行组合。

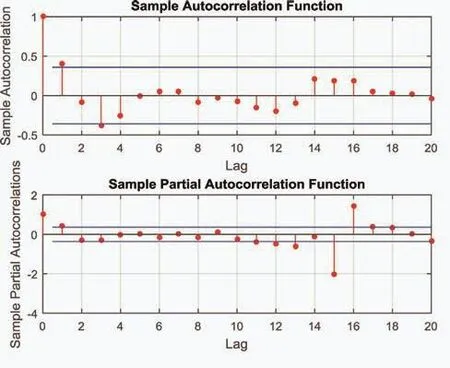
图4 平稳数据的ACF和PACF图

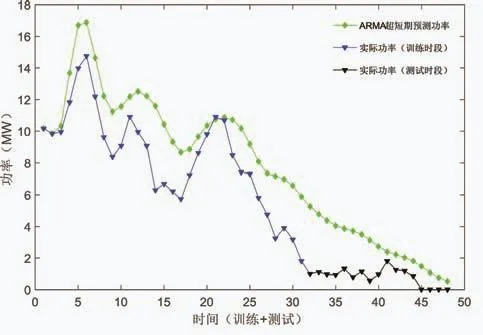
图5 ARIMA超短期功率预测结果和实际功率曲线图

图6 卡尔曼模型所得预测结果和实际功率以及短期预测功率曲线图

图7 各单体算法和组合算法预测误差对比图

图7是3种单体算法和组合算法预测误差的对比图。其中ARIMA算法和卡尔曼算法所得误差的变化较剧烈；组合算法在每个点上的误差几乎都能达到最小。通过计算得组合预测误差的方差为4.2519，ARIMA算法误差的方差12.7935，多元回归算法误差的方差为6.2052，卡尔曼算法误差的方差为11.8062。所以，可以验证Var（e）min≤min（Var（ei））。

图8是各单体算法和组合算法的超短期预测结果对比图。可见最小方差组合算法所得预测结果均优于3种单体算法预测结果。

本文采用云南省份8个风电场近半年的数据对每种算法进行训练，每种方法选取不同的预测长度进行分析，预测长度分为 15min、1h、2h、3h、4h。表1展示了不同预测长度下每种算法的预测误差和准确率。

实验结果表明，当预测时长小于2h时，单体算法ARIMA算法表现最优；当预测时长在2～4h时，组合算法表现最优。

图8 各单体算法和组合算法的超短期功率预测结果对比图

表1 不同预测步长不同算法的预测误水平

结论

风电场的输出功率在一定程度上呈现随机性和波动性的特点，并且随着预测时长的变大，这种随机性和波动性的特点表现尤为突出。单体算法会导致某些预测点存在较大的误差，组合算法会在某种程度上降低误差。单体预测算法是组合算法的基础，其预测结果的好坏直接影响组合预测的效果，本文将不同的输入信息分别输入到3种单体算法中，并利用了单体算法自身的预测优势，有效避免了采用相似的单体预测算法进行组合带来的模型冗余。在预测时段较长时，本文提出组合算法弥补了单体算法建模预测的不足。在进行超短期预测时，多元回归算法能较准确预测出实际功率未来4h的变化趋势，但在纵向上多元回归所产生的预测功率和实际功率还存在较大的误差；ARIMA算法能够较好地拟合未来4h实际功率的纵向波动，从而在多元回归算法的基础上，降低预测功率和实际功率的纵向误差，卡尔曼算法能较好地对未来4h的实际功率预测值进行动态修正。针对西北和部分南方区域，超短期考核第4h点，组合算法表现较优。