电池剩余放电时间预测
2018-09-20黄旭罗志超肖一啸王敬前
黄旭,罗志超,肖一啸,王敬前*
(1.陕西服装工程学院 经济管理学院,陕西西安,712046;2.陕西服装工程学院基础部,陕西西安,712046)
引言
铝酸电池作为电源被广泛应用于工业,军事,日常生活当中。铅酸电池从充满电开始以恒定电流强度放电,电压随放电时间单调下降,直到额定最低保护电压Um(题中为 9V),这个过程中电压随时间应化的关系被称为放电曲线。而电池通过较长时间的使用或者放置,充满电后的荷电状态会发生衰减。根据这一特性,本文对电压、时间和电流的关系进行研究并建立了曲线拟合模型,来预测不同电流强度及状态下的放电时间。现给出两个附件:
附件 1是同一生产批次电池出厂时以不同电流强度放电测试的完整放电曲线的采样数据。
附件 2是同一电池在不同衰减状态下以同一电流强度从充满电开始放电的记录数据。
根据附件中所给出的数据,解决以下三个问题:
问题1:利用初等函数表示同一生产批次出厂电池以9种放电电流放电时的放电曲线。从附件一中按从Um开始按不超过0.005V的最大间隔提取231个电压样本点并求出其平均相对误差(MRE)在电压为9.8V,电流强度分别为的条件下的电池剩余放电时间。
问题2:建立以20A到100A之间任一恒定电流强度放电时的放电曲线的数学模型。
问题3:预测附件2中电池衰减状态3的剩余放电时间。
1 问题分析
需要根据附件 1中的数据求得各个放电强度中的平均相对误差,通过曲线拟合建立不同电流强度下电压与电池剩余时间的关系,及不同电压下电流强度与电池剩余时间的关系。问题的特点在于数据量大,难点在于在附件1中要取231个样本点求得各曲线方程的平均相对误差,及MRE评估模型精度。
1.1 问题1分析
通过SPSS软件,根据曲线拟合求得各放电强度下的放电曲线方程,建立了电池放电时间和电压的关系,然后再有合EXCEL软件根据题目中对平均相对误差(MRE)取231个样本点,求得各放电曲线的平均相对误差,最后在固定电压为9.8V、电流强度为30A~70A的放电条件下,通过放电曲线方程预测得到电池放电时间,进而求得保护电压9V时,已知放电时间减去预测放电时间得到电池剩余放电时间。
1.2 问题2分析
通过SPSS软件建立20A~100A的电流强度与电压、时间的关系的数学模型求得其MRE,代入55A的电流强度,求得电压与放电时间、剩余放电时间的关系,从而用表格和图形绘制出放电曲线。
1.3 问题3分析
根据附件二所给的数据利用SPSS软件建立出衰减状态3下电压与时间的的线性方程,从而求得电池衰减状态3下的放电时间进而求得电池剩余放电时间。
2 模型的建立与求解
2.1 问题1的解决方案
本节运用SPSS软件,根据曲线拟合求得各放电强度下的放电曲线方程,建立了电池放电时间和电压的关系,然后再有合EXCEL软件根据题目中对平均相对误差(MRE)取 231个样本点,求得各放电曲线的平均相对误差,最后在固定电压为9.8V、电流强度为30A~70A的放电条件下,通过放电曲线方程预测得到电池放电时间,进而求得保护电压9V时,已知放电时间减去预测放电时间得到电池剩余放电时间。
2.1.1 问题1模型的建立
根据对附件 1所给出的数据,画出电流强度为20A~100A的图表,如图1至图9所示。通过SPSS软件,可以拟合出多项式函数、指数函数、对数函数等,采用P值检试和数值大小比较,选用二次函数作为模型,所以建立的模型为:

以下(1)至(9)给出电流强度为20A~100A时,具体的放电曲线表达式、MRE和电压为9.8V时的剩余时间。
(1)当电流强度为20A时,拟合的放电曲线如图1所示:
放电曲线方程为:
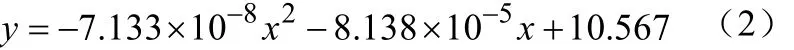
MRE电池的剩余时间为942.08891。
(2)当电流强度为30A时,拟合的放电曲线如图2所示:
放电曲线方程为
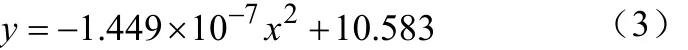
MRE电池的剩余时间为618.68669。
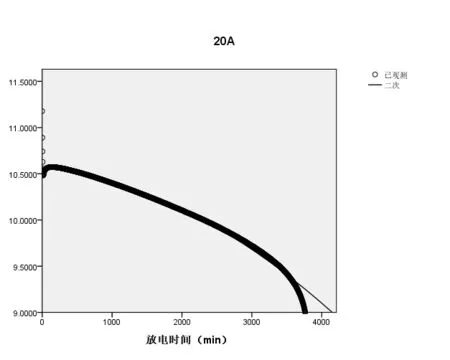
图1 20A时的放电曲线
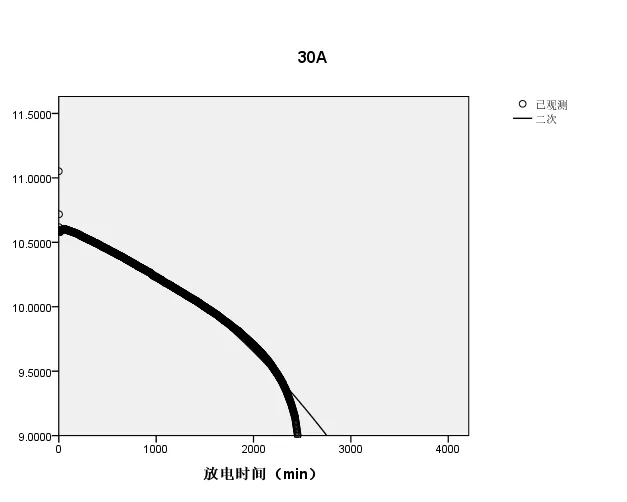
图2 30A时的放电曲线
(3)当电流强度为40A时,拟合的放电曲线如图3所示:
放电曲线方程为

MRE电池的剩余时间为443.08988。
(4)当电流强度为50A时,拟合的放电曲线如图4所示:
放电曲线方程为
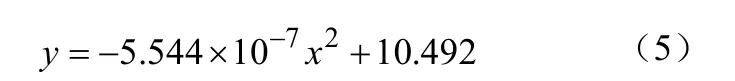
MRE= 0.012208979;当y9.8V时,x= 966.1274,电池的剩余时间为341.8726。
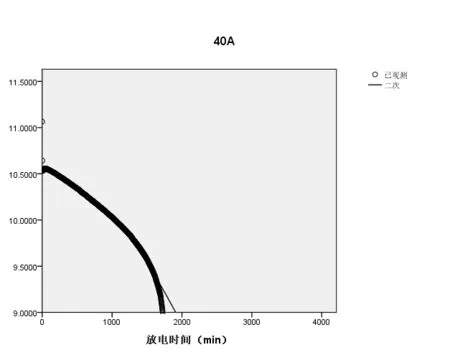
图3 电流强度为40A时的放电曲线
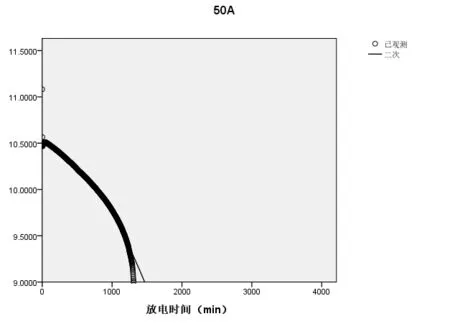
图4 电流强度为50A时的放电曲线
(5)当电流强度为60A时,拟合的放电曲线如图5所示:
放电曲线方程为
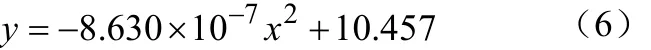
MRE电池的剩余时间为292.91203。
(6)当电流强度为70A时,拟合的放电曲线如图6所示:
放电曲线方程为
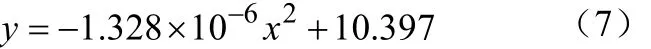
MRE电池的剩余时间为274.45014。
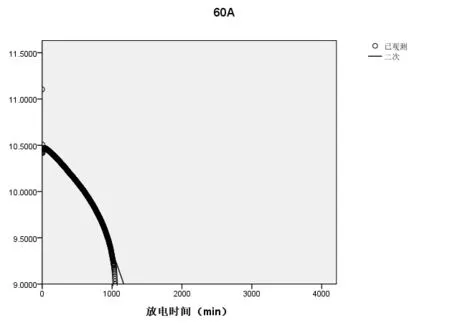
图5 60A时的放电曲线
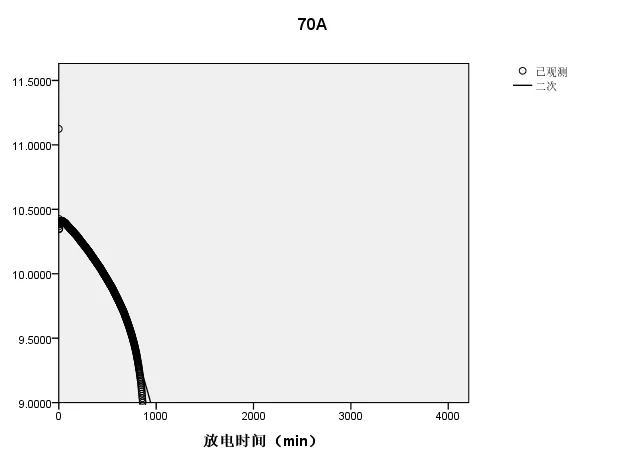
图6 70A时的放电曲线
(7)当放电强度为80A时,拟合的放电曲线如图7所示:
放电曲线方程为
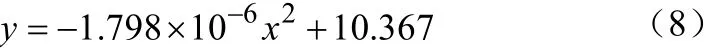
MRE电池的剩余时间为255.24913。
(8)当放电强度为90A时,拟合的放电曲线如图8所示:
放电曲线方程为
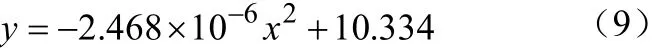
MRE电池的剩余时间为233.77035。
(9)当放电强度为100A时,拟合的放电曲线如图9所示:
放电曲线方程为
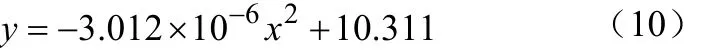
MRE= 0.076401288;当y9.8V时,x= 317.39805,电池的剩余时间为220.60195。
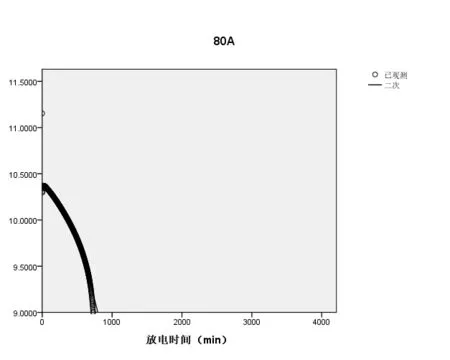
图7 80A时的放电曲线
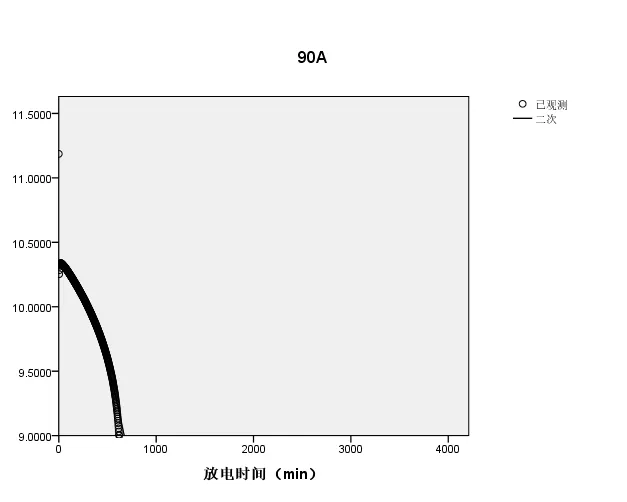
图8 90A时的放电曲线
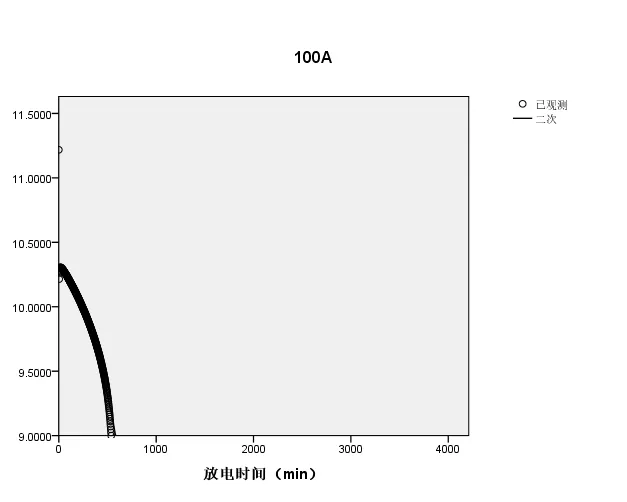
图9 100A时的放电曲线
对电流强度为20A~100A计算得的曲线方程,MRE及电池剩余放电时间如下表1所示:
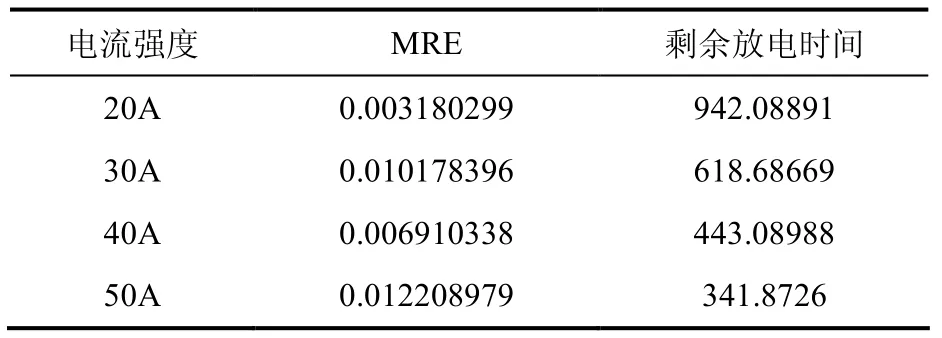
表1 MRE及电池剩余放电时间
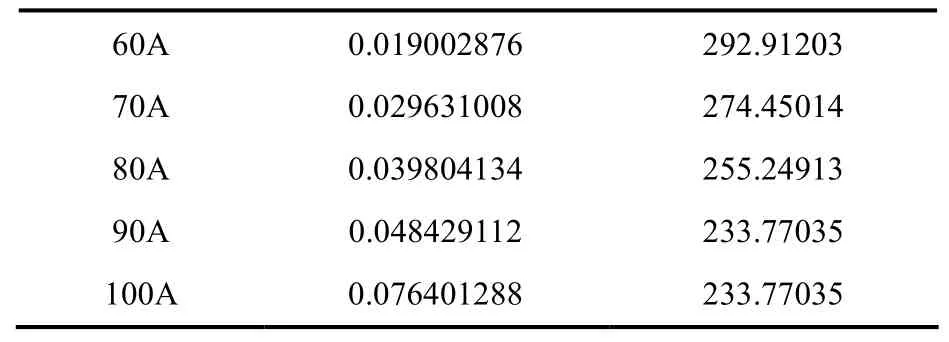
60A 0.019002876 292.91203 70A 0.029631008 274.45014 80A 0.039804134 255.24913 90A 0.048429112 233.77035 100A 0.076401288 233.77035
利用矩阵表示电流强度为20A~100A曲线方程,如下:

由矩阵可以看出,在电流强度为20A~100A曲线方程中,当x>0时,为减函数,说明随着时间的增加,电压随之减少,与实际相符。而表1中基本上所有的MRE<0.006,说明所拟合的函数精度高。
对电流强度与部分剩余放电时间的关系如下表2所示:

表2 电流强度与部分剩余放电时间
对电流强度与电池剩余时间关系的折线图由下图10所示:
图10 电流与剩余放电时间的关系
由表2和图10可以看出,同一电池在同一电压下,随着电流强度的逐渐增加,时间逐渐减少。
2.2 问题2的解决方案
通过SPSS软件建立20A~100A的电流强度与电压、时间的关系的数学模型求得其MRE,代入55A的电流强度,求得电压与放电时间、剩余放电时间的关系,从而用表格和图形绘制出放电曲线。
2.2.1 问题2模型的建立
由问题一建立的二次函数模型可以得到电压与时间的模型为:

可以得到模型中a、b、c随电流的应化而应化,因此可以通过SPSS建立a、b、c与电流强度关系的表达式:
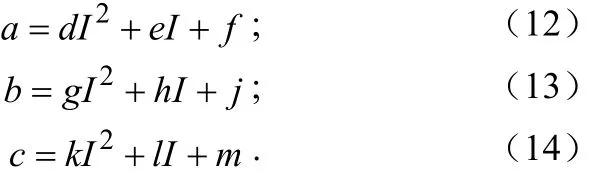
所以,可以建立出电压与时间、电流的模型:
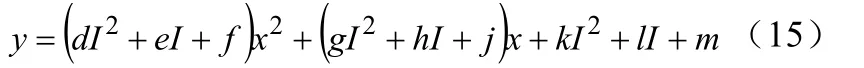
因此可以建立电压、电流与时间的方程为:
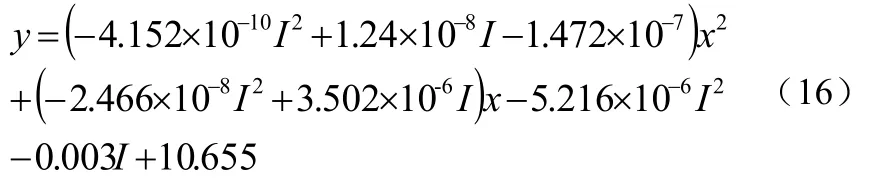
(1)电流强度为20A~100A时与放电曲线模型中的各项系数拟合有有如下表3所示:
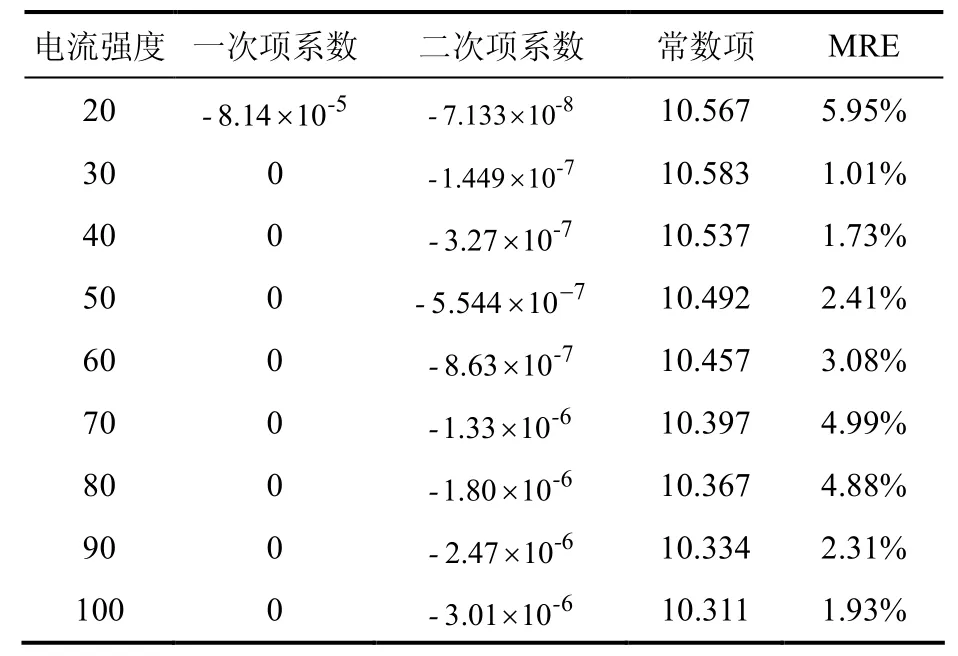
表3 电流强度与放电曲线数学模型中的各项系数拟合结果
观察表3可得,当x>0时,为减函数,说明随着电流强度的增加,各项系数也逐渐减少。
(2)电流强度为55A时,放电时间与部分电压的关系如下表4所示:
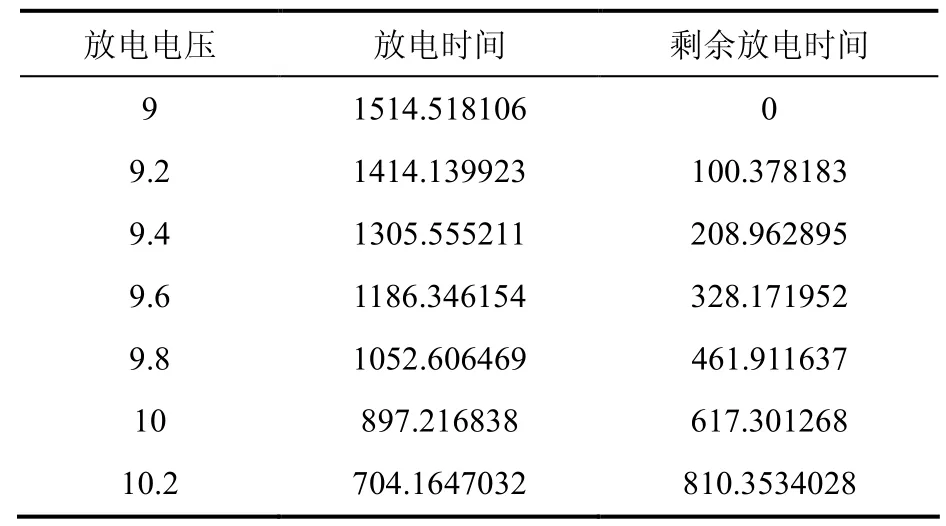
表4 放电时间与部分电压的关系
电流强度与电池剩余时间的折线图如下图10所示 :观察表4与图10可得,当电流为55A时,放电时间的逐渐减少,电压逐渐增加,与实际相符。
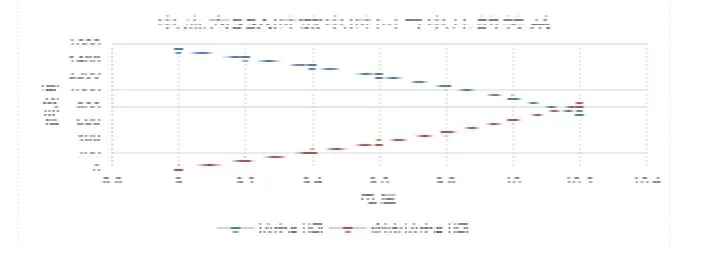
图10 放电时间与电压的关系
2.3 问题3的解决方案
本节主要根据附件二所给的数据利用SPSS软件建立出衰减状态3下电压与时间的的线性方程,从而求得电池衰减状态3下的放电时间进而求得电池剩余放电时间。
2.3.1 问题3模型的建立
根据附件二所给的数据利用SPSS软件建立出衰减状态3下电压与时间的的线性方程:
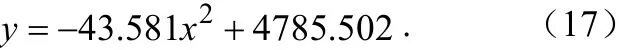
求得当电压为9v时所得时间为1255.441,因此电池衰减状态3的剩余放电时间为659.241。
3 有束语
(1)本文利用了图像分析法和对比分析法,可以更清晰的分析出图像中的信息。
(2)本文所建立的任务定价模型也可以应用于其他服务定价,推广度较高。
(3)本文在选取应量时应对影响任务标价的各个应量进行检试与选取,从而能挑选出与任务标价关系更为密切的应量。
