基于BP神经网络的草原矿区表层土壤N/P高光谱反演模型
2018-09-19卢志宏刘辛瑶常书娟杨胜利赵薇薇刘爱军
卢志宏,刘辛瑶,常书娟,杨胜利,赵薇薇,杨 勇,刘爱军
(1.铜仁学院,贵州 铜仁 554300; 2.内蒙古农业大学,内蒙古 呼和浩特 010018;3.内蒙古自治区草原勘察规划院,内蒙古 呼和浩特 010051)
土壤氮(N)、磷(P)是土壤主要的养分元素之一,是植物生长发育必需的矿质元素,也是生物地球化学循环的重要组成元素,对维持生态系统稳定性具有重要意义[1]。土壤N、P往往成为植物生长发育的限制因子[2-3],二者既相互独立又互相影响[4],其比值是研究生态系统营养结构变化、生物多样性和地球化学循环的基础[5-6]。利用高光谱反演土壤、植物的碳、氮、磷、钾等元素含量均已获得成功,而利用高光谱反演N/P比的研究尚未见文献报道。
土壤高光谱是土壤各种理化性状(有机质、无机元素、水分、质地和孔隙度等)的综合反应,营养元素与其他理化性质的光谱吸收峰之间相互重叠[4],呈现冗余的波长信息,严重影响模型的拟合和预测精度[5]。由于电磁干扰、样品背景等因素增加了大量的冗余信息,一定程度上也降低了估算的准确性。然而,高光谱具有分辨率高、波段信息量大的特点,在估算土壤有机质、氮素、水分和重金属含量等方面具有较大优势[6-7]。因此,土壤属性含量定量反演模型研究中,变量消除和筛选是高光谱在估算土壤理化性质模型构建中的重要环节。
在光谱分析中,多元回归模型可以实现降维和剔除冗余信息[8-9],显著提升光谱分析的精度和可靠性[10-12]。线性回归算法通过提取原始光谱信息的主要成分进行建模[13],算法有主成分分析(PCA)、偏最小二乘法(PLS)[14-15]等方法,核心是获得最大方差的线性特征集,缺点是损失了部分信息[16]。非线性模型因其更加接近客观规律,得到了广泛的应用,而非线性模型的复杂性也促进了变量的筛选。BP神经网络可以学习和模拟任意复杂的非线性函数,结合多元逐步回归筛选高光谱信息,建立基于多元逐步回归变量筛选后的BP神经网络模型,可有效提高土壤属性的反演能力,为草原矿区土壤管理策略提供参考意见,对典型草原植被受氮和磷限制的快速分析提供拟解决方案。
1 研究区概况与数据获取
1.1 研究区概况
内蒙古锡林郭勒典型草原的胜利煤田矿区为温带半干旱草原气候,冬季寒冷干燥,夏季温暖湿润,年平均气温为 0.3 ℃,年均降水量为336.9 mm,集中在5-8月,无霜期大约为150 d,年潜在蒸发量为1 600~1 800 mm。土壤为典型栗钙土,钙积层约25~35 cm。植被群落中建群种为大针茅(Stipagrandis)和羊草(Leymuschinensis)。植被群落的总覆盖度大约为30%~40%[17]。
1.2 数据获取
2014年7月至9月中旬,以煤炭采集区为矿区中心,向矿区四周7个不同方向辐射设置调查样线(图 1),在距矿区外边界0~5.5 km距离内每隔0.5 km,采集土样,共计70个,每个样品采集点采集5个表层(0-10 cm)土样,去掉植物根系、石块等残渣,混合均匀后带回实验室风干,一部分研磨、过筛,全氮采用凯氏蒸馏法,全磷采用钼锑抗比色法;另一部分测定土壤高光谱反射率。
高光谱反射率采用美国ASD便携式光谱仪进行测定,光谱范围为350~2 500 nm,重采样间隔为10 nm,选取天气晴朗、光照条件好的时段进行测量,探头垂直于土壤表面,距离土壤表面20 cm,测定前使土壤表面平整,每个土样测试前用白板定标,连续测定10次,间隔时间为5 s,取平均值作为实际反射率数据。
2 研究方法
2.1 BP神经网络模型
BP神经网络模型是一种非线性映射模型,具有完整的数学算法,理论上能够无限逼近任意复杂的非线性函数[18-19],网络结构一般分为输入层、隐含层和输出层,隐含层可以有多层,通过连接权值和阈值传递信号[19]。

图1 研究区位置和取样点示意图Fig. 1 A diagram of the study area and sampling location
2.2 模型构建
基于全波段的土壤高光谱反射率,波段较多,且不同波段之间存在严重的自相关。本研究采用多元逐步回归方法进行变量筛选,以降低变量间的多重自相关,减少BP神经网络模型的复杂程度[20]。在MATLAB 2014 a环境下,将高光谱地面反射率作为输入向量,N/P比值作为目标向量,按照70∶15∶15的比例设定训练集数据、验证集数据和测试集数据,尝试建立预测模型。实际应用中,通常不区分训练集和验证集,合称为训练集。

input_train = data(1,1∶60)'; output_train = data(1,1∶60)'; %训练集input_test = data(2∶end,61∶70)'; output_test = data(2∶end,61∶70)'; %测试集采用试凑法来确定隐含层节点数,隐含层层数设置代码如下(以4层为例):for m=1∶30; %m为第1隐含层节点数for n=1∶30; %n为第2隐含层节点数for o=1∶30; %o为第3隐含层节点数for p=1∶30; %p为第4隐含层节点数net =newff(inputn,outputn,[m n o p],{'tansig','purelin'});...... endendendend
在网络学习过程中,为了消除输入样本间的量纲差异,更好地进行学习,对样本进行了归一化处理:
(1)
式中:xi和xi′为归一化前后的第i个向量元素,xmax和xmin为对应向量的最大值和最小值。建模过程中,学习速率为0.000 1,精度要求为0.004,训练次数为1 000,输入层和隐含层之间的传递函为正切S型函数tagsig,隐含层与输出层之间的传递函数为对数S型函数logsig,网络采用Levenberg-Marquardt优化算法进行优化,模型精度评价指标采用决定系数(R2)和均方根误差(RMSE),R2越大,模拟效果越好[21],RMSE越小模拟效果越好[22]。R2、RMSE计算公式如下:
(2)
(3)
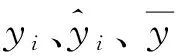
3 结果与分析
3.1 表层土壤N/P分布特征
试验所测的N/P范围为0.090 0~1.054 3,标准差为0.156 8,平均值为0.541 2,变异系数为28.97%,属于中等变异[23];偏度系数为0.060 8,峰度系数为4.877 6属于正态分布(图2a);由分位数图可知,N/P存在低频度的大于或小于平均值的极端值(图2b),结合范围参数说明试验区N/P差异较大。
3.2 地面高光谱反射率特征
研究区不同土壤采样点光谱特征曲线数值分布特征较为一致,土壤高光谱反射率在可见光范围内呈快速上升态势,由于组成土壤的固体颗粒物使光谱曲线表现出逐渐增加的特征;在近红外至红外波段区间,受长波辐射的增温及土壤含水的影响,导致表层土壤反射率对温度的敏感程度增加,在1 100、1 400、1 900 nm附近,有3个较为明显的水分吸收谷(图 3)。
3.3 多元逐步回归分析
在MATLAB 2014a平台上应用多元逐步回归算法进行了多元一次回归分析,回归系数为0的波段未进入多元逐步回归模型,最终从216个波段中筛选出70个波段用来建立BP神经网络模型,其中包括2个可见光波段,68个红外光波段(图4)。土壤中N、P原子震动对特定波段具有明显的影响,2个可见光波段和68个红外光波段反应了N、P原子共同震动对高光谱产生的影响。

图2 表层土壤N/P正态分布Fig. 2 The normal distribution of the N to P ratio in surface soil

图3 表层土壤高光谱反射率Fig. 3 Spectral reflectance of soil samples
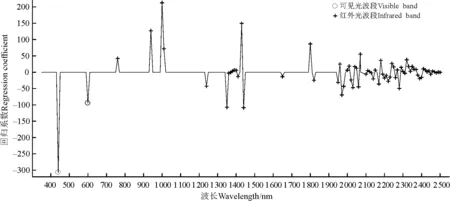
图4 土壤N/P与土壤反射率回归系数Fig. 4 Regression coefficients of soil N to P ratio with soil reflectance
3.3 单隐含层BP神经网络模型
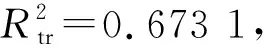
3.4 双隐含层BP神经网络模型
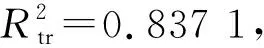
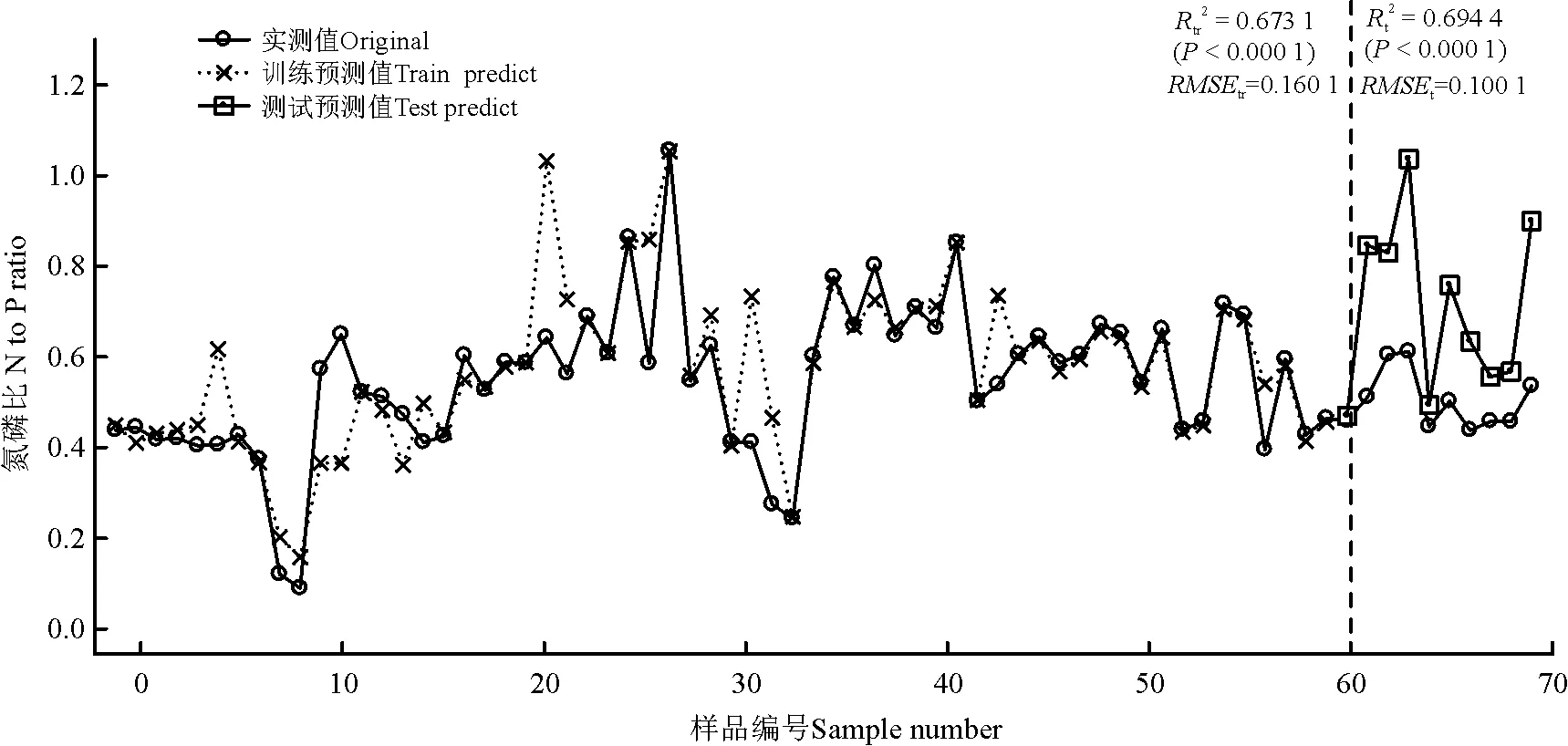
图5 单隐含层BP神经网络拟合与预测效果Fig. 5 The result of fitting and prediction using a single hidden layer-containing BP neural network model



图6 双隐含层BP神经网络拟合与预测效果Fig. 6 The result of fitting and predictions using a double-layered BP neural network model
3.5 3层隐含层BP神经网络模型

3.6 4层隐含层BP神经网络模型

3.7 不同模型的比较
随着BP神经网络模型隐含层层数的增加,训练数据和测试数据的拟合优度均先增加后降低,隐含层层数为3时达到最大;训练数据的均方根误差随隐含层层数增加呈先降低后增加的变化趋势,测试数据的均方根误差呈现波动变化,隐含层层数为3时最小;最大拟合误差除4层隐含层网络的较小外,3层隐含层模型的最大拟合误差、最小拟合误差、平均拟合误差、最大预测误差、最小预测误差和平均预测误差均最小,因此,综合考虑训练数据和测试数据的拟合优度、均方根误差等,认为3层隐含层BP网络模型在模拟和预测典型草原矿区表层土壤氮磷比(N/P)效果最好。
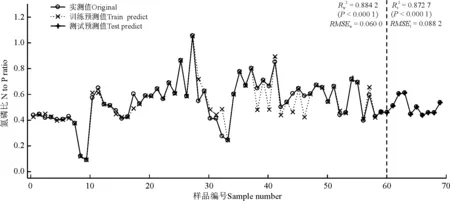
图7 3层隐含层BP神经网络拟合与预测效果Fig.7 The result of fitting and prediction using a three hidden layer-containing BP neural network model
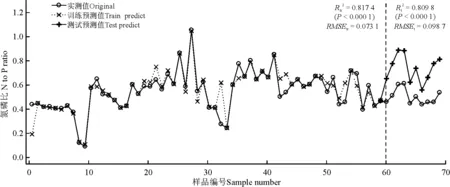
图8 4层隐含层BP神经网络拟合与预测效果Fig. 8 The result of fitting and prediction using a four hidden layer-containing BP neural network model
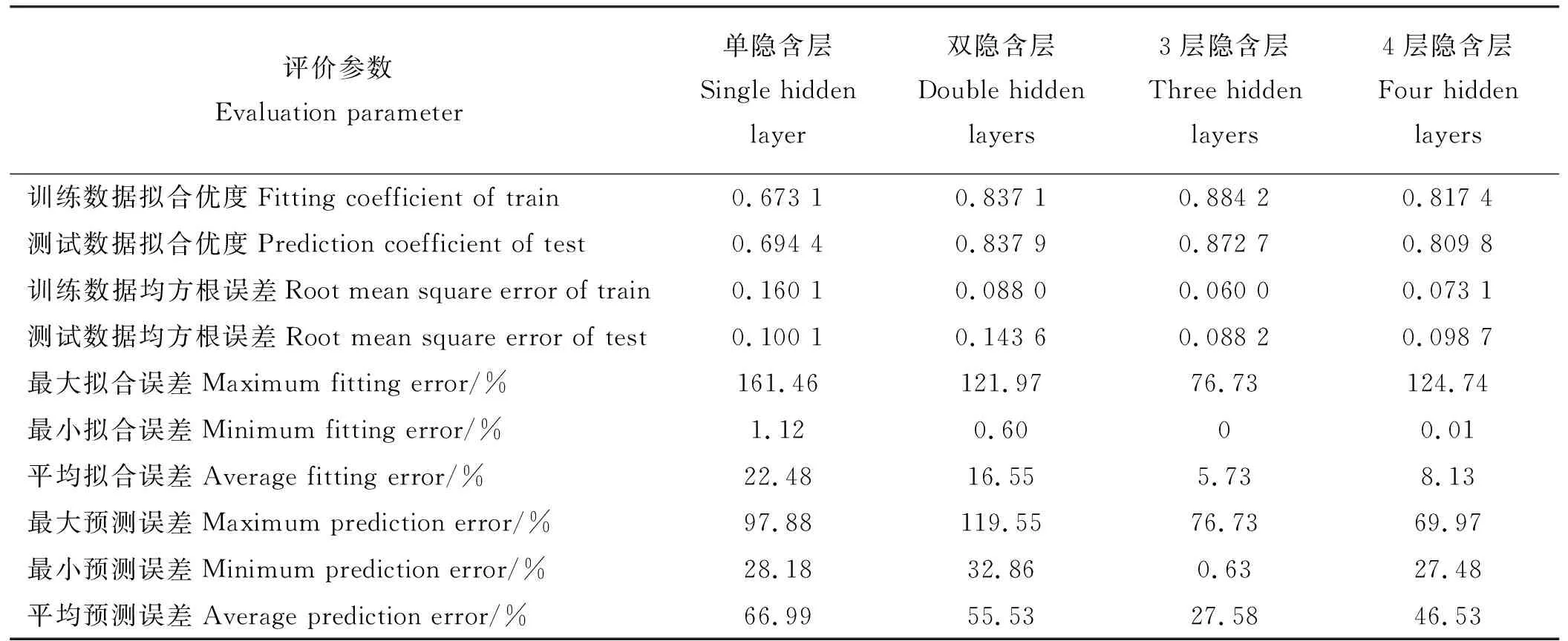
评价参数Evaluation parameter单隐含层Single hidden layer双隐含层Double hidden layers3层隐含层Three hidden layers4层隐含层Four hidden layers训练数据拟合优度Fitting coefficient of train0.673 10.837 10.884 20.817 4测试数据拟合优度Prediction coefficient of test0.694 40.837 90.872 70.809 8训练数据均方根误差Root mean square error of train0.160 10.088 00.060 00.073 1测试数据均方根误差Root mean square error of test0.100 10.143 60.088 20.098 7最大拟合误差Maximum fitting error/%161.46121.9776.73124.74最小拟合误差Minimum fitting error/%1.120.6000.01平均拟合误差Average fitting error/%22.4816.555.738.13最大预测误差Maximum prediction error/%97.88119.5576.7369.97最小预测误差Minimum prediction error/%28.1832.860.6327.48平均预测误差Average prediction error/%66.9955.5327.5846.53
4 讨论与结论
土壤高光谱是土壤各种理化性质(有机质、氧化铁、水分、质地和孔隙度等)的综合表现,两者之间存在着密切的关系[24-25],土壤不同养分元素之间以及与其他理化性质的光谱吸收峰之间相互重叠,呈现合频和倍频现象[4],因此土壤高光谱中存在大量冗余的波长信息。筛选出不同土壤性质的敏感波长,有利于构建较高精度的估测模型。李伟等[26]认为神经网络预测碱解氮、速效磷、速效钾含量效果均优于偏最小二乘法模型。蒋烨林等[25]认为神经网络模型在稳定性和精度上优于PLSR和SMLR模型,其中以预测全氮含量的二阶微分神经网络模型效果最优。本研究比较分析了不同隐含层模型的预测精度,筛选了预测N/P最佳的网络模型,同样认为神经网络模型在拟合和预测中能够获得较好的效果。
理论上认为BP神经网络可以实现以任意精度逼近任意连续函数,其输入层和输出层由实际问题决定,因此隐含层的层数和每层节点数影响着网络的模拟与预测精度[27]。随研究对象复杂程度的增加,可以通过增加隐含层层数提高学习精度,但同时导致预测能力下降[28]。隐含层层数的增加,意味着可供筛选的模型呈指数级增加,筛选最优模型的时间增加。本研究采用的是穷举法进行筛选,单隐含层模型设置节点数取值范围为1~30,重复100次,共计进入筛选的模型为3 000个。双隐含层、3层隐含层、4层隐含层模型穷举的模型为302、303、304次,且分别重复100、30、10次,共计9万、81万、810万个,尤其是4层隐含层网络在没有开启并行运算模式时运行时间长达30 d,效率极低。因此多隐含层最优模型的筛选方法需要进一步探索。王泽平[29]在预测水质时发现,3层隐含层BP模型预测精度高于GA-BP 模型、双隐层BP 模型、单隐含层BP模型,3层隐含层BP模型拟合精度、整体预测精度最高,并认为通过增加隐含层层数可以有效提高网络的预测精度,使多隐含层BP网络模型预测精度毫不逊色于GA-BP模型。梁慧等[22]比较了线性回归模型和BP神经网络模型在积雪面积比例的反演精度,认为神经网络的稳定性较优,均方根误差远小于线性模型,R2较大;本研究经过大量网络的筛选,也取得了较小的均方根误差(RMSE)和较高的拟合优度(R2),最终认为3层隐含层的BP神经网络在预测内蒙古典型草原矿区表层土壤N/P时效果最好。
陆地生态系统常受氮磷的限制[30],磷的增加速率低于氮的增加速率[31],使氮磷比发生变化,植物进行相应的调整和采取应对的保护策略[32-33]。土壤N/P和植物N/P之间的不一致维系着植物需求和土壤供给能力[34],一般认为N/P低于21预示着氮限制[35],Yang等[34]认为内蒙古典型草原土壤为氮限制,通过氮添加可以提高土壤氮供应能力和植物氮含量。本研究区域土壤N/P低于21,与Yang等[34]研究结果一致。王炜等[36]认为禁牧初期可以提高草地归还能力,提高物种丰富度,增加群落复杂性。通过高光谱BP神经网络模型反演土壤N/P,可以快速测定土壤氮磷比变化情况,为草地管理如禁牧时间、载畜量等提供可靠依据,提高草地利用效率,保证草地生态系统的稳定。本研究应用多元逐步回归分析在216个高光谱波段中筛选出70个波段,降低了变量维度,建立的3层隐含层网络获得了较高的拟合优度和预测能力。
综上所述,通过多元逐步回归可以有效降低模型变量输入纬度,简化神经网络模型复杂程度,适当增加隐含层层数,可获得较高的拟合优度和预测精度,得到隐含层节点数为6、3、10的3层隐含层BP神经网络模型可以为草原矿区土壤N/P提供快速拟合与预测的方法,为草地科学管理提供有效依据。
致谢:感谢中国农业科学院草原研究所郭利彪副研究员对高光谱特征分析的指导,感谢暨南大学粤港澳中枢神经再生研究院李邦博士后及乌江学院孟金柱副教授在论文修改过程中给予的帮助。
