基于Matlab/Simulink的区间二型自组织模糊逻辑控制器工具箱

， ，，

(贵州大学机械工程学院，贵州贵阳550025)

0 引言

模糊控制技术最为新型的智能型控制之一，已得到了科学界的广泛认同。1997年，基于模糊数学理论产生的模糊控制技术被开发成T1FLC工具箱收入到MATLAB中，并且作为商业工具箱应用到实际控制中。而随着模糊理论的不断发展，模糊控制器系统已由T1FLC发展成为二型自组织模糊逻辑控制器[1]，但T2SOFLC编程过程复杂繁琐。为解决这个问题，本课题延续MATLAB商用T1FLC工具箱的设计风格，以基于Simulink为实验平台结合用户图形界面形式编写T2SOFLC工具箱程序。该方式省去了繁琐的程序编写，以直观且简洁地界面操作构建被控系统的控制器，缩短了控制系统的研发周期，并且便于模糊控制系统的参数寻优。

1 二型自组织模糊逻辑控制系统

1975年L.A.Zadeh教授继续对已提出的模糊集合进行扩展[2]，进一步将语言值集合的模糊隶属度函数模糊化形成三维的隶属度函数，极大增强了集合描述模糊性、多重不确定性信息的能力，也使得模糊集合更加贴近客观世界中语言变量的描述。而为解决单纯的模糊逻辑控制器不具备适应过程持续变化的能力，尤其是在处理复杂多变系统的情况下。在1979年，Procyk和Mamdani把自组织机构(SOC，Self-Organizing Controller)加入到模糊控制器的设计中，研究自组织模糊逻辑控制器如何在短时间内学习控制被控系统，这为后来的T2SOFLC结构奠定了基础[3]。

1.1 二型模糊逻辑控制系统

T2FLS主要由模糊化、规则库、推理机、降阶、解模糊化五部分组成。而相较于T1FLC，T2FLC的模糊化过程中采用二型隶属度函数为三维数学模型，包含多重不确定信息，造成了解模糊化部分的复杂化。因此在解模糊化前多出一个隶属度函数降阶过程。

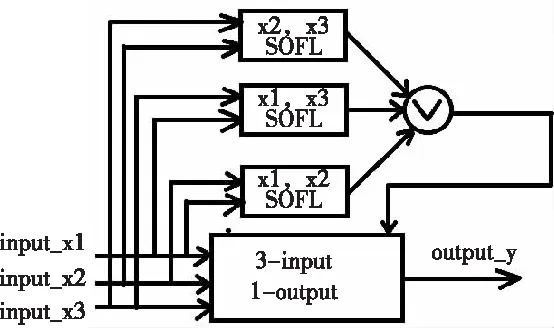
图1 三输入单输出模糊逻辑控制器系统的分解图

由于模糊逻辑系统的性能函数仅以二维形式显示，因此我们使用[4]文献介绍的方法将m输入/ n输出T2FLS结构分解为多个2输入/ 1输出的子系统，然后将其输出所述那样聚集在一起进行降阶运算。如图1所示三输入单输出T2SOFLC已被分解成3个两输入/一输出子系统。

1.2 自组织模糊控制结构原理

SOC能够调整和修改控制规则以输出期望的控制响应，构成了T2SOFLC的第二级[5]。目前，工具箱只激活了自组织模糊逻辑控制机构，它能在控制过程中不断矫正控制规则，从而达到所期望的控制效果。T2SOFLC是在T2FLC的基础上增加了性能测量、控制量校正和规则修正3个环节[6]，如图2所示。

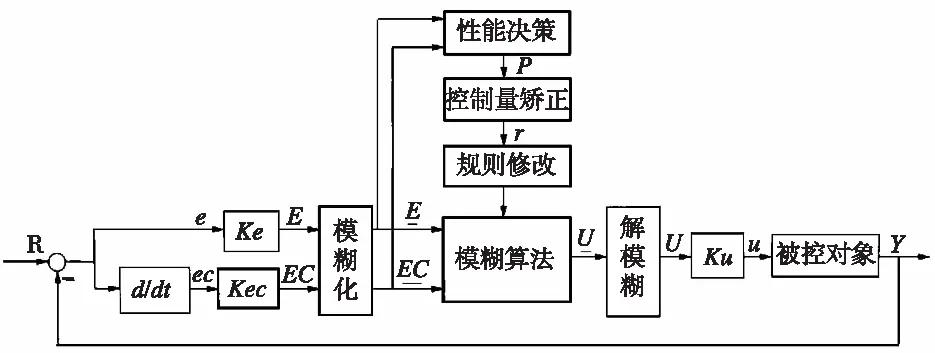
图2 SOC结构

控制规则的修正过程采用直接修改规则本身的方法。在此考虑有一定时滞的系统，设时滞为mT，当前采样时刻为nT，那么过去(n-m)T时刻的控制作用对当前nT时刻的输出产生影响。设E(nT-mT)，EC(nT-mT)，U(nT-mT)分别表示过去的偏差、偏差变化和控制量，而U(nT-mT)+P(nT)表示修正后的控制量，将这些量模糊化处理，得到

E(nT-mT)=F(e(nT-mT))

(1)

EC(nT-mT)=F(ec(nT-mT))

(2)

E(nT-mT)→CE(nT-MT)→U(nT-mT)

(3)

E(nT-mT)→CE(nT-MT)→U(nT-mT)+P0(nT)

(4)

V(nT-mT)=F(U(nT-mT)+P0(nT))

(5)

其中，F表示模糊化过程。

每条模糊规则Ei×ECi×Ui(i为规则数)可用3条语言值隶属度代替，对所有的规则进行如上修改后，如有新的规则产生则再增加一条新规则加到系统中去。

2 T2SOFLC工具箱

目前T2SOFLC工具箱主要由设置系统参数的自定义类、辅助类的用户交互界面和Simulink环境下的运算模块三部分组成，而最终形成T2SOFIS的结构层次如图3所示。

图3 T2SOFIS结构层次图

由主界面、自组织机构选择界面、二型隶属度函数编辑界面以及规则编辑界面和自组织模糊控制机构性能隶属度编辑界面及性能评价规则编辑界面共五大操作界面组成。它们的操作关系如下所述：

如图4(左)所示为控制工具箱的主界面，我们可以在界面上设置变量名称以及选择其他模糊算法。双击变量函数图框可以进入二型隶属度函数的设置界面如图5(左)所示，也可以在该界面中选择添加自组织控制结构。目前已具备的只有SOC_FLS(代表Self-Organizing Fuzzy Logic Control)，其他GD(Gradient Descent，梯度下降)，GA(Genetic Algorithm，遗传算法)，NN(Neural Networks，神经网络)选项目前都是不可编辑状态如图4(右)所示。也可以单击Rule Editor图框进入二型模糊控制系统的规则编辑界面，如图5(右)所示。图4和图5中所列工具箱操作界面涉及的主要函数名称如表1所示。

图4 工具箱主界面(左)及其自组织结构选择界面(右)

图5 二型隶属度函数编辑界面(左)与规则库编辑界面(右)

若需要添加自组织控制机构，点击主界面内add self-organizing按键后可选择添加自组织结构，进入自组织模糊控制的性能隶属度函数编辑界面，点击下一步可以设置隶属度函数的性能以及评价规则设置，如图6所示。该工具箱界面所用到的主要函数名称如表2所示。

表1工具箱主界面及其SOC选择界面主要函数名表

函数名作用举例T2SOFLS建立一个T2SOFLS控制器T2SOFLS(“name”)T2SOFLS.addInput加入或修改输入变量T2SOFLS.addInput(“name”)T2SOFLS.delInput删除一个输入变量T2SOFLS.delInput(“name”)T2SOFLS.addOutput加入或修改输入变量T2SOFLS.addOutput(“name”)T2SOFLS.delOutput加入或修改输入变量T2SOFLS.delOutput(“name”)T2SOFLS.method修改系统运算方法T2SOFLS.method(“TR”,”weight”)T2SOFLS.add2mf选择其一输入变量加入一个隶属度函数T2SOFLS.add2mf(“input1”,“name”)T2SOFLS.addUmf选择其一输入变量加入或修改一个隶属度函数T2SOFLS.addUmf(“input1”,“name”,“trimf”,[0 0.5 1],1)T2SOFLS.addLmf选择其一输入变量加入或修改一个隶属度函数T2SOFLS.addLmf(“input1”,“name”,“trimf”,[0 0.5 1],1)T2SOFLS.del2mf选择其一输入变量删除一个隶属度函数T2SOFLS.del2mf(“input1”,“name”)T2SOFLS.add2rule添加一条控制规则T2SOFLS.add2rule(“input1”,“NB”,”in-put2”,”NB”,”output1”,”PB”)T2SOFLS.del2mf选择其一输入变量删除一个隶属度函数T2SOFLS.del2rule(“input1”,“NB”,”in-put2”,”NB”,”output1”,”PB”)

图6 SOC的隶属度函数编辑界面(左)与性能规则库编辑界面(右)

表2工具箱界面SOC设置参数界面主要函数名表

函数名作用举例T2SOFLS.addSOCmf选择其一输入变量加入或修改一个性能隶属度函数T2SOFLS.addSOCmf(“input1”,“name”)T2SOFLS.delSOCmf选择其一输入变量删除一个性能隶属度函数T2SOFLS.delSOCmf(“input1”,“name”)T2SOFLS.addSOCrule选择其一输入变量加入或修改一个控制规则T2SOFLS.addSOCrule(“input1”,“NB”,”in-put2”,”NB”,”output1”,”PB”)T2SOFLS.delSOCrule选择其一输入变量加入或修改一个控制规则T2SOFLS.delSOCrule(“input1”,“NB”,”in-put2”,”NB”,”output1”,”PB”)

3 仿真研究与结果分析

在现实中，麻醉师常使用药理模型来描述和理解药物的新陈代谢系统。现代药理模型包含两个类别：药物动力学(PK)和药效学(PD)。前者描述了组织中的药物浓度作为时间与药物剂量时间关系，而后者描述血液中的药物浓度与药效之间的时间关系。以此基于多变量麻醉药物模型，我们使用T2SOFLC工具箱来实现复杂多变的被控系统所需控制效果。

3.1 多变量麻醉模型

我们建立Atracurium(ATR)静脉注射控制肌肉松弛度和调控Isoflurane药物浓度(ISO)降低病人血压值的多变量患者麻醉模型来描述控制器工具箱在维持平均动脉压(MAP)和肌肉松弛度的目标值的情况下，具有适应性地控制ATR的注射与ISO的浓度的能力。

ATR和ISO两种麻醉药物的多变量药理模型描述如下[27-28]：

(6)

其中U1为ATR药物的注药速率；U2为ISO药物浓度。

G11(s)为ATR药物的PD数学模型：

(7)

其中τ1=1 min是时滞时间(药物注入到生效时间间隔)，K1=1，T1=4.81 min，T2=34.42 min，T3=3.08 min，T4=10.64 min。

G22(s)为ISO麻醉药物数学模型：

(8)

其中MAP是动脉血压均值；τ2是时滞时间；T5是时间常数和K2=-15mmHg/%。

由于ATR药物对于BP信号影响太小，所以之间的相互作用可以忽略。然而ISO药物浓度间接对于肌肉的松弛度是重要的影响因素，其相互间的影响数学模型可以用以下方程描述：

(9)

其中τ1=1 min是时滞时间(药物注入到生效时间间隔)，T6=2.83 min，T7=1.25 min，K4=0.27 min。

3.2 控制器设计

参照文献[7]中生理指标的临床资料推算出T2SOFLC的区间二型隶属度函数不确定因素的特征变量值以及模糊控制规则建立模糊逻辑控制器。如图7所示的输入变量肌肉松弛度误差的二型隶属度函数的模糊集。

图7 肌肉松弛度误差输入变量的区间二型隶属度函数集合

3.3 控制结果

如图8所示为4个输入2个输出的T2SOFLC在无噪声干扰情况下的模拟结果表明，该控制器能够校正规则使病人的肌肉松弛度和血压达到设定值，验证了其模糊逻辑工具箱的控制效果，且与之前所做各类模糊逻辑控制所得各项生理指标参数稳态误差的实验结果都相差无几。

图8 4个输入2个输出T2SOFLC在无噪声下的模拟结果

4 结论

本课题是以台湾元智大学智能型实验室在病人麻醉手术领域的研究资料和各类模糊控制器程序为依托，改变T2SOFLS应用环境，以Simulink为实验平台并创建用户操作界面完成T2SOFLS工具箱，并再次应用于全身麻醉药物的非稳态病人麻醉模型。其实验结果如图8所示，该工具箱达到了良好的收敛效果。

我们针对工具箱的不足提出了如下几点：自组织控制结构的应用理论有很多种，我们将会集众家之所长采用更多的控制方法如梯度下降法、遗传算法学习和神经网络学习法等[8-11]；实现Simulink的控制器模块与所建工具箱用户图形界面间更多的数据交互，开发更多的内嵌函数对数据实现分析处理，获得更多直观的信息；在Simulink环境下构建更多复杂多变的被控系统，对工具箱进行系统性的性能分析。