一种三自由度并联平台运动学研究

， ，

(中国科学院长春光学精密机械与物理研究所航测二部，吉林长春130000)

0 引言

为适应非六自由度的机构设计，同时希望机构能具有并联机构的运动响应快、结构刚度高、误差小等优点，目前研究热点逐渐移动到少自由度并联机构[1]。少自由度并联机构的本质是在六自由度的基础上，在机构中加入了不同形式的约束[2]。通过不同的约束的布置形式将机构的自由度约束至合适的范围。由于机构的约束形式各异，使机构表现为不同的特性。少自由度并联机构具有驱动件少、结构简单、控制容易的特点[3]。

在针对国内外稳定平台和并联平台结构分析的基础上[4-6]，借鉴现有的稳定平台结构、驱动方式和控制方式等，结合稳定平台所要求的结构简单、成本低、承载能力大以及可移动性好等特点，设计出了三自由度并联稳定平台，其结构示意图如图1。

图1 机构总体方案

此机构特点为升沉电动推杆上平台和下平台的中心，两个转动电动推杆分别等距分布在两个转动自由度方向上。上下平台支点在平衡位置等距离(100 mm)布置(推杆与立柱平行)。平台的转角运动极限范围是±20°，升沉运动的极限范围是45 mm。两个电动推杆关节结构分别为：UPS(双端为球铰，中间移动副)和RPS(一端球铰，一端虎克铰，中间移动副)。

1 运动学分析

1.1 正运动学分析

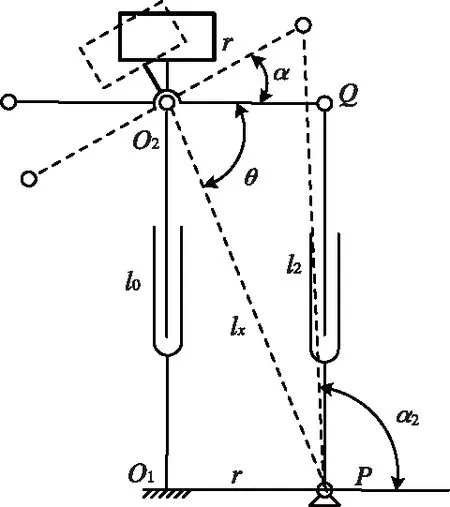
图2 单轴旋转运动简图

本文首先对纵摇四杆机构进行单独的分析，对于一端球铰一端铰链的横摇方向，应为铰链的约束，其四杆在同一平面内，机构简图可以简化为图2所示。

其中坐标系O1-x1y1z1为基准坐标系。在机构中，r=100 mm为平台中心到电动推杆立柱的距离，为O1P1、O1P2、O2Q1、O2Q2的距离，l0、l1、l2分别为升沉电动推杆、横摇电动推杆和纵摇电动推杆的的长度，其取值范围360 mm～520 mm。

图中α为平台转动的角度，根据闭环矢量法建立方程：

(1)

根据公式(1)可得到：

(2)

利用正余弦公式可计算出：

(3)

机构设计中：r为电动推杆和平台连接处距平台中点的距离为100 mm；l0和l2为升沉电动推杆的长度，其取值范围为360 mm～520 mm；角θ为∠P2O2Q2，其值随升沉电动推杆杆长的伸长量而改变，其值的运动范围为1.30 rad～1.38 rad。将值带入公式(3)可得：

(4)

在双轴进行转动时，机构简图如图3。

图3 单轴旋转运动简图

角α只受电动推杆l0、l1、l2的长度影响，角度值已由公式(4)得到。角β即受电动推杆l1的影响，又因为电动推杆l2会导致面O2Q1P1转动。受到l0、l1、l2综合影响。根据闭环矢量法列出公式：

(5)

因为在此转动方向上O2Q1P1和O2O1P1不在同一平面，适用y轴上的方程需要根据两个平面的分割线O2P2分为两个方向。新列出闭环矢量方程：

(6)

根据结构模型，已知点O2处为虎克铰，虎克铰的两个转动副相互垂直。当电动推杆l2推动角α在某一定值时，O2Q1始终在垂直于O2Q2方向进行旋转，同时面O2Q1P1垂直于O2Q2，β′为在面O2Q1P1中平台转动的角度，根据余弦定理可得：

(7)

β=arccot(cotβ′·cosα)

(8)

1.2 逆运动学

因为空间机构计算较为复杂，逆运动学采用D-H法计算。D-H法研究机构各连杆之间的位移关系，通过计算相邻连杆坐标系之间的转换关系得到转换矩阵，使用转换矩阵表示其关系。通过坐标系的等价齐次变换矩阵，建立机构的运动方程。稳定平台机构见图2。在坐标系1和坐标2中，各点的坐标为：

1P1=(r，0，0)T2Q1=(r，0，0)T

1P2=(0，r，0)T2Q2=(0，r，0)T

(9)

1O1=(0，0，0)T2Q2=(0，0，0)T

将O1-xyz设为1坐标系(基准坐标系)，将O2’-x’y’z’进行平移，绕基准坐标系y轴旋转β角，x轴旋转α角，可得坐标系2。坐标转换公式为：

(10)

(11)

(12)

电动推杆长度l1为：

(13)

(14)

(15)

电动推杆长度l2为：

(16)

2 运动规律计算

图5 横摇角度与推杆伸长量关系

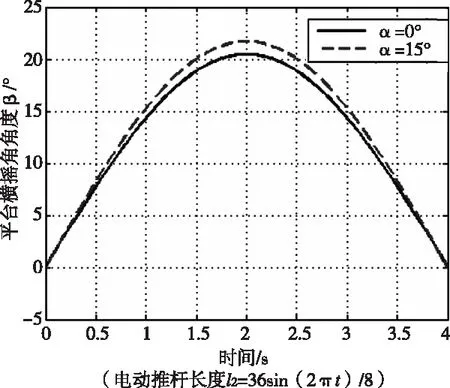
图6 α不同时，耦合造成的平台角度差别(电动推杆以相同规律运行)

根据本课题推导出的运动学模型，将所求得的公式带入运动学的Simulink仿真程序。在实际系统中，平台工作在横滚角度为6°，纵摇角度为15°，升沉为40 mm的正弦运动中，根据计算出的公式对实际工作条件下并联平台进行仿真计算。其中a为角度α，b为角度β，l1为电动推杆1的伸长量，l2为电动推杆2的伸长量。当升沉电动推杆停留在中点时，将正信号带入到正逆运动学数学模型中可得，当纵摇角度为6°时，电动推杆移动量为10.45 mm。当横摇角度运动到15°时，电动推杆移动25.89 mm。平台角度与电动推杆的伸缩量的关系如图4和图5。

图6展示了纵摇角度在0°位置和15°位置时，电动推杆以l2=36 sin((2πt)/8)运动时，平台角度因纵摇方向改变，耦合作用导致的平台横摇角度的差别。实线是纵摇角度为0°时，电动推杆伸长时平台角度。虚线为纵摇角度为15°时，电动推杆伸长时平台角度。由此看出在本课题中平台耦合对角度影响较大，在最大有2°左右的耦合影响。

在运动过程中，升沉运动对需要三个电动推杆完成运转动作的同时对升沉运动的运动量进行补偿。升沉运动占系统运动总功率中最大的一部分，其摆动和转动直接影响到升沉电动推杆、横摇电动推杆和纵摇电动推杆的伸长量和运动规律。升沉运动不仅仅只线性影响横摇电动推杆和纵摇电动推杆的伸长量，由于升沉运动改变了横摇运动和纵摇运动的杆长，电动推杆在推动平台转动时的伸长量也有影响。

图7 升沉运动影响曲线 图8 耦合对转动的影响

机构以周期为8 s幅值为15°的正弦信号进行运动时，升沉量为0 mm和正负40 mm对电动推杆的伸长量如图7所示。升沉运动不仅仅只线性影响横摇电动推杆和纵摇电动推杆的伸长量，由于升沉运动改变了横摇运动和纵摇运动的四杆机构中的杆长，其对电动推杆在推动平台转动时的伸长量会产生影响。当升沉分别为40 mm、零点位置和-40 mm时，平台转动15°需要的电动推杆伸长量如图8所示。可见机构运动处于小角度(±15°)范围运动，升沉运动对角度的耦合最大0.002°。

因为系统的三个自由度之间相互耦合的影响。因此在建立系统时，需要将运动学方程导入控制器的算法中。对于高精度的稳定平台来说，横摇和纵摇间相互耦合较大，不可忽略。而升沉运动对平台转动角度的耦合较小，最大仅为7″。

图9 平台位置对传动比的影响

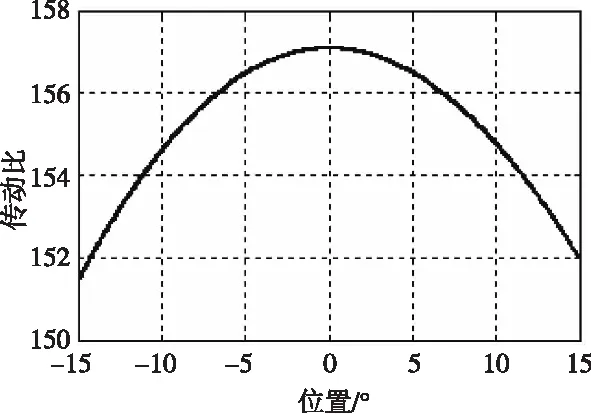
图10 平台位置与传动比变化规律

电动推杆中，电机经过传动比为1的齿轮传动连接丝杠，则电机角度φ与电动推杆的伸长量l的关系为：φ=2·π·l/p，其中p为丝杠导程为4 mm。传动比可以用电机端转速除以末端平台转速得到。经过运动学的计算仿真，求得由电机端至平转端的传动比。当平台以15°正弦进行运动可以看出，平台在水平位置，即平台和推杆垂直时，传动比最大为157。在MATLAB中可以求到传动比随平台运动关系曲线如图9所示，平台位置与传动比的关系如图10所示。

3 总结

针对一种三自由度并联平台进行了正逆运动学的计算，并通过simulink对其运动规律进行仿真计算。文中部分数据采用实际机构参数尺寸进行计算，得到的运动规律以及此种并联平台的运动特性，对特征相似的并联平台的研究有一定的参考价值。