有向相依网络的可控性研究
2018-09-19陈世明程运洪邓兵
陈世明,程运洪,邓兵
(华东交通大学 电气与自动化工程学院,江西 南昌 330013)
在过去几十年中,复杂网络研究吸引了许多来自不同科学领域学者的关注[1]。而以往的工作主要集中在对网络拓扑结构复杂性及其与网络动力学行为之间关系的研究,通过对复杂网络拓扑性质、复杂网络演化模型以及动力学行为的分析,揭示出隐藏在复杂系统中的一系列共同规律,对于把握复杂系统的宏观特征及调节复杂系统上的动力学行为都将具有重要意义[2-3]。随着对复杂网络研究的进一步深入,复杂网络可控性的研究得到了充分的关注与重视。Lin[4]给出了线性时不变控制系统“结构”和“结构可控性”的概念,并通过研究找到了结构可控性的充要条件;Liu等[5]基于线性时不变控制系统的结构可控性理论,对实际复杂系统进行了研究并建立了网络结构可控性模型;Jia[6-7]发现了两种不同的网络控制模式:集中式控制和分布式控制;同时基于控制能力和随机抽样算法对有向复杂网络的结构可控性做了进一步探索,随后一些研究者通过改变连接边的方向实现了网络可控性的优化[8-10]。目前复杂网络可控性研究已经取得了众多的重要成果,但复杂网络控制方面的研究仍然处于起步阶段,还有很多未解决的理论问题,例如结构可控性理论无法适用于无向网络、权重网络和时变网络的可控性等问题。针对结构可控性理论仅适用于有向网络的局限性,Yuan[11]引入了严格可控性(exact controllability)的概念,证明完全控制复杂网络所需的最少控制器数目由网络矩阵特征值的最大重数决定,并提出了利用矩阵初等变换甄别网络中需要被独立控制的节点的方法,通过对大量真实网络和模型网络的计算结果表明了严格可控性理论的有效性和实用性;Li[12]针对实际网络的分型特征,运用严格可控性理论对分型网络的可控性进行了分析。基于单层有向网络和无可控性进行的研究已取得了较大突破。但现实中的网络通常是相互依存的,例如,公交–地铁网络、电力–通信网络、电力–供水网络等,且通过研究已经发现相依网络的动态特性如级联失效[13-17]、扩散现象[18]、演化博弈动力学[19]、同步性[20]等,均明显区别于单层网络。怎样合理地控制相依网络将是面临的重要挑战。Yuan[21]运用严格可控性理论对多重网络的可控性进行了研究,发现在多关系网中存在主导关系网,其结构和连接权重对于整个网络的严格可控性起主导作用;在多层网中,不同层间的连接方式以及疏密程度对整个网络的严格可控能力都有重要的影响,并且发现在层间加入少量连接能够大大提高整个网络的可控能力。Nie[22]分析了多层网络中层间连边结构对网络可控性能的影响,研究发现层间连边比例较小时,网络最少驱动节点的数目随着连边度相关性的增加而减小,层间连边同配性强的网络易于控制;当层间连边比例较大时,则会出现相反的情况,层间连边异配性强的网络易于控制。然而以上研究仅分析了网络层间的连接方式及网络层间连接边的度相关性对无向相依网络可控性的影响,却未考虑到实际网络中存在有向网络相互依存的情况,例如在交通网络与供电网络中,某一时间内列车的运行方向是定向的,同时供电系统按照列车运行的线路提供电力支持保证其正常运行。在供电网络中某一处发生故障会通过网络之间的相依关系,将其传递到交通网络中从而导致经过这条线路的列车都无法运行,反之亦然。这样在某个网络中产生的故障会因为彼此间的相依关系,使得故障在两个网络之间相互蔓延,从而对网络造成更大的破坏,由此表明有向相依网络间的相依关系对整个有向相依网络有重要影响。为了探究有向网络间相依关系对网络的影响,本文首先构建了基本的有向相依网络模型,并结合严格可控性理论,给出了基于最少控制输入的可控性评判指标;其次,针对相依方式对有向相依网络可控性产生的影响,基于经典的有向随机网络(DER)和有向无标度网络(DSF),构建了DERDER、DER-DSF、DSF-DSF 3类有向相依网络模型,并研究了随机相依方式下3类网络的可控性能;最后,基于随机相依方式下对网络可控性的分析,提出了3种有向网络的相依方式:最高入度与最高出度节点相依(HI-HO)、最高入度与最低出度节点相依(HI-LO)、最低入度与最低出度节点相依(LI-LO),且在既定的3种相依方式下对网络的可控性进行了仿真分析。
1 有向相依网络可控性
1.1 有向相依网络
有向相依网络由两个有向子网络(子网络A和子网络B)通过双向连接线连接而成,表示子网络A中的节点,节点数为;表示子网络B中的节点,节点数为,子网络之间的双向连接线为网络相依边,其余单向连线为内部边。F表示节点相依比例。F包括和,其中表示子网络A的相依节点数占子网络A总节点数的比例值,表示子网络B的相依节点数占子网络B总节点数的比例值,即


图 1 有向相依网络Fig. 1 The interdependent directed network
1.2 严格可控性
在现代控制理论中,如果通过一些控制变量的输入能使一个系统从任意初始状态达到理想状态,我们称这个系统是可控的。这里只考虑线性时不变系统并且假设系统内部未发生动态变化。有向相依网络状态方程为
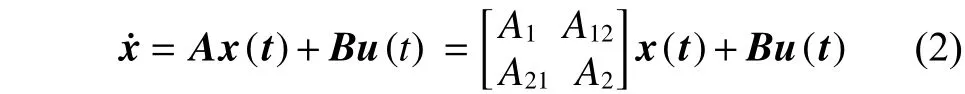
定理1 对于一个可控系统来说,最少控制输入个数是系统矩阵特征值中具有最大代数重数的特征值所对应的几何重数。

1.3 理论分析
对于满足状态方程(2)的系统来说,其节点总数是不变的且为,若使得系统满足其可控性,需通过外部控制输入作用于系统节点。假设得到外部控制输入作用的节点个数为,未作用的节点个数为,则

对于可控系统来说,必然存在一个得到外部控制输入作用节点的最小个数,记为,使得系统达到可控要求,并且未作用的节点个数达到最大,记为,得

从而可得


然而需要确定能够达到控制效果所需的最少控制输入个数。在这里将最小控制输入个数定义为达到系统可控性要求时,输入矩阵B秩的最小值,即

若满足状态方程(2)的系统是可控的,那么由PHB判定定理可知,对矩阵A的任意特征值,下式恒成立:

式中I为单位矩阵。
根据矩阵不等式关系得:

进一步得
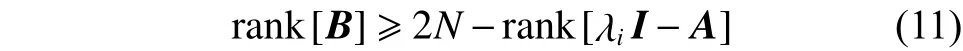
上式满足恒成立关系,则:

进一步可得



最后可得:




图 2 有向相依网络可控性Fig. 2 Controllability of the interdependent directed network
2 随机相依方式下网络可控性的仿真与分析
本文基于经典的有向随机网络(DER)和有向无标度网络(DER),构建了DER-DER、DER-DSF、DSF-DSF 3类有向相依网络模型。同时在随机相依方式下,对不同相依比例的DER-DER网络可控性进行了独立仿真实验。
在随机相依方式下,通过对4组不同相依比例的DER-DER网络可控性进行多次仿真,其中网络规模,T为实验次数,;相依比例为。从图3(a)中可以发现在相依比例时,在区间内出现明显的波动,即网络可控性在这一范围内出现很大的随机性;同时结合图3(b)、3(c)、3(d)可知,在相依比例、0.4、0.8时,同样在一定范围内出现较大的波动。这表明,在同一相依比例下,随机的相依方式使得网络可控性表现出明显的差异性,即有向网络的相依方式直接影响着网络的可控性。
通过对比以上4组不同相依比例下的网络可控性发现,随着相依比例F的逐渐增加,逐渐减小,即随着相依比例的增加,网络可控性逐渐增强。为了充分证明相依方式直接影响着有向相依网络可控性,我们在随机相依方式下对连续相依比例的3类有向相依网络的可控性进行了仿真分析。

图 3 单一相依比例下DER-DER网络的可控性Fig. 3 Controllability of DER-DER network with a single dependency ratio
在随机相依方式下,通过对连续相依比例的DER-DER、DER-DSF、DSF-DSF这3类有向相依网络的可控性进行仿真,如图4(a)所示,就DERDER有向相依网络而言,随着相依比例F的逐渐增加,总体呈现逐渐减小的趋势,但由于相依方式的随机性,DER-DER有向相依网络中存在,的情况,同时在图4(b)所示的DER-DSF有向相依网络与图4(c)所示的DSF-DSF有向相依网络中均呈现与图4(a)相同的变化规律,即网络可控性在随着相依比例增加而增强的过程中会出现一定程度的波动,从而表明有向相依网络的可控性不仅与相依比例有着紧密相关,更与有向网络的相依方式有着密不可分的关系,上述分析为有向相依网络可控性的研究提供了充分条件。


图 4 连续相依比例下网络的可控性Fig. 4 Controllability of the network under continuous dependency ratio
3 有向相依网络的相依方式及其可控性对比分析
基于随机相依方式下对有向相依网络可控性的分析,本文提出了有向网络之间的3种相依方式:最高入度与最高出度节点相依(HI-HO)、最高入度与最低出度节点相依(HI-LO)、最低入度与最低出度节点相依(LI-LO),同时针对3种相依方式构建了如图5所示的简单有向相依网络模型并分析了其可控性。


图 5 有向相依网络的相依方式Fig. 5 Dependent way of the interdependent directed network
针对提出的3种有向网络相依方式,在DERDER、DER-DSF、DSF-DSF 3类有向相依网络中对网络可控性进行了仿真对比。如图6(a)所示,在DER-DER有向相依网络中对3种既定相依方式而言,均呈现随着相依比例F增大而减小的趋势,同时在图6(b)所示的DER-DSF有向相依网络与图6(c)所示的DSF-DSF有向相依网络中,的变化趋势与图6(a)相同,即在同一有向相依网络中对任一既定相依方式来说,网络可控性会随着相依比例的增加而逐渐增强。在图6(a)所示的DER-DER有向相依网络中,针对相同相依比例,对3种既定相依方式下的网络可控性进行对比发现(LI-LO)<(HI-LO)<(HI-HO),同时在图6(b)所示的DER-DSF有向相依网络与图6(c)所示的DSF-DSF有向相依网络中,在同等相依比例下有(LI-LO)<(HI-LO)<(HI-HO),即在同一网络中相同相依比例下,基于最小入度与最小出度节点相依的有向相依网络可控性最强,而基于最大入度与最大出度节点相依的有向相依网络可控性最弱。
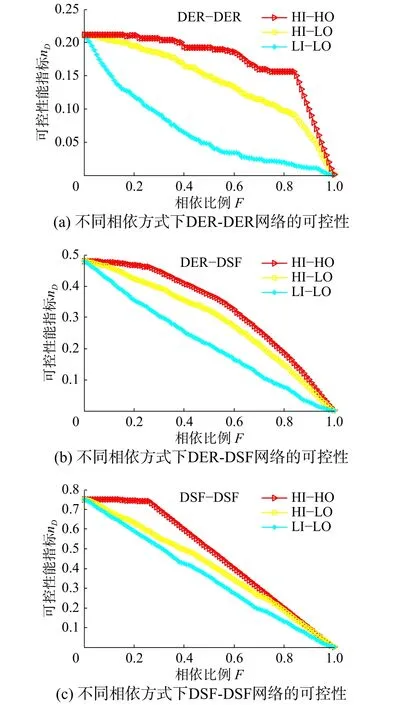
图 6 不同相依方式下有向相依网络可控性Fig. 6 Controllability of the interdependent directed network under different dependent way
4 结束语
相互依存的复杂网络广泛存在于实际复杂系统中,且往往存在有向网络之间的相依,本文首先构建了基本的有向相依网络模型,并结合严格可控性理论,给出了基于最少控制输入的可控性评判指标;考虑相依方式对有向相依网络可控性产生的影响,本文基于经典的有向随机网络(DER)和有向无标度网络(DSF),构建了DER-DER、DER-DSF、DSF-DSF 三类有向相依网络模型,并在4组不同相依比例下,研究了随机相依方式下的DER-DER网络的可控性能,研究发现,随着相依比例的增加,网络可控性逐渐增强。但每组相依比例下的网络可控性均会在一定范围内出现大幅的波动。为了进一步证实相依方式影响着网络的可控性,通过在随机相依方式下对连续相依比例下的3类有向相依网络可控性进行了仿真,我们发现随着相依比例的逐渐增加,网络可控性总体均呈现逐渐增强的趋势,但由于相依方式的随机性,网络可控性在增强过程中会出现明显的波动情况,即有向网络的相依方式对网络可控性产生着重要影响。
基于分析本文提出了3种有向网络的相依方式:最高入度与最高出度节点相依(HI-HO)、最高入度与最低出度节点相依(HI-LO)、最低入度与最低出度节点相依(LI-LO),同时就提出的3种相依方式在3类有向相依网络中对网络可控性进行了仿真对比,且通过对比发现,在同一网络中同等相依比例下,基于最低入度与最低出度节点相依的有向相依网络可控性最强,而基于最高入度与最高出度节点相依的有向相依网络可控性最弱。研究证实了有向网络相依方式密切影响着网络的可控性,且得到3种相依方式下有向相依网络可控性的强弱关系,这为构建强可控性能的实际有向相依网络提供了参考依据。
