不等精度数据融合的最优权值与参数估计方法

张志敏

(中国人民解放军92941部队44分队，辽宁葫芦岛 125001)

0 引言

不同类型和不等精度数据的融合是测量数据融合处理中的常见难题，也是研究的热点问题［13］。测量数据融合处理的主要目的就是提高参数估计的精度，建立合适的数学处理模型，给出高效可靠的融合算法，建立既能够适合数学处理，又能够体现物理过程、工程特征的融合处理模型是关键。模型包括测量数据的模型和目标轨迹模型，而测量数据建模又包括测量误差建模与测量目标真实信号建模。不同类型和不等精度数据是指观测数据中关于待估参数的函数关系不同、各阶导数也不同［45］。因此，针对不同类型不等精度的观测数据的融合处理，使用不同的加权方法，会对参数估计结果造成较大的影响。因此针对不同的应用背景研究适合的加权融合处理方法成为提高不同类型和不等精度数据的融合参数估计精度的关键。

对于线性回归模型，已有文献 ［6］证明了其参数估计，以及不等精度测量数据的唯一最优加权原则 。但是对于非线性回归模型，当前的研究结果都是利用线性回归模型的处理思维以及迭代算法，求解非线性回归问题，在基于观测数据的随机误差是独立同分布等精度条件下推导的［7-9］，不进行加权处理，或直接采用线性模型的高斯－马尔科夫定理对不同类型的观测数据进行加权处理，对于参数估计的精度的提高存在很大的局限性。非线性回归模型的非线性程度会对参数估计的偏差、方差等因素产生影响，因此通过什么方法可以降低模型的非线性程度，成为长久以来非线性模型研究领域的难点。文献［10］通过引入非线性模型的参数效应曲率和固有曲率，使降低曲率相当于降低模型非线性程度，采用曲率表征模型的非线性程度，目前该理论已成为非线性模型定量分析的理论基础，为非线性回归模型的研究提供一种新的思路，极大地促进了不同类型不等精度测量数据非线性融合的权值问题的研究。

对于不同种类的不等精度测量数据融合处理的权值与参数估计的问题，根据对参数估计偏差和均方误差进行分析的结论，从理论上证明了对于非线性模型在不同类型不等精度数据融合处理时，最优融合权值不仅与数据本身精［6］度有关，而且与模型的结构、导数相关联，且线性模型高斯－马尔科夫定理不再适用。给出了多结构多元非线性融合模型的最优权值与参数估计的计算方法，最后通过四个算例的对比验证，可以证明该方法是有效可靠的。

1 不等精度观测数据线性融合的最优权值和参数估计

针对参数βp×1的估计问题，假如有两类线性测量数据，其观测方程如下所示:

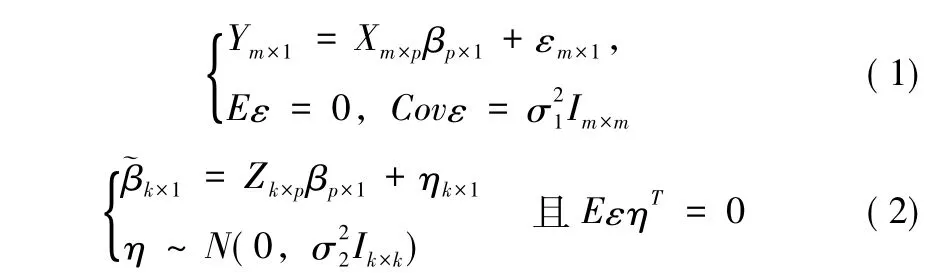
对于两类不等精度线性观测数据融合模型 (1)－(2)的参数估计，构造如下模型所示:

定理 1: 记 λi，1，λi，2，i=1，…，p分别为矩阵 XTX，ZTZ的特征值，那么融合模型的最优权值和参数估计形式如下所示:

证明:1)由 (3)关于参数β求一阶偏导数，得到正规方程为:

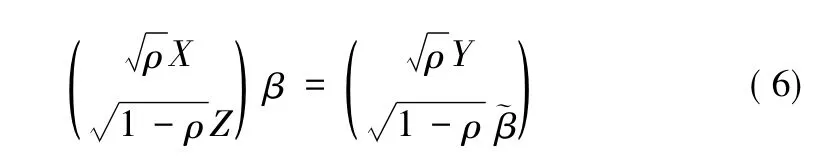
因此，得到1)。

2)将 (4)式代入，并由模型 (1)、(2)的假设，计算即可得到 (5)的第一式。

即定理1的结论3)成立。

定理1的结论3)具有重要的应用价值。在处理实际问题时，(1)、(2)一般为不等精度的测量数据，在这些数据的融合处理时，数据的加权对于数据处理精度具有重要影响。结论3)说明不等精度的线性观测数据融合处理时唯一最优融合权值由测量数据的精度决定，这本质上仍然是线性模型最小二乘估计的Gauss－Markov定理。

2 不等精度观测数据非线性融合的加权和参数估计

在很多估计问题中，往往要考虑异类不等精度非线性观测数据的融合处理［2］。这里，我们提出的异类数据，具体指观测数据关于待估参数的函数关系不同，因而它们的模型结构也不一样，参数估计的精度对其依赖程度自然也是不同的。则不同结构的观测数据的权值也应该是不同的。

2.1 非线性模型参数估计的方差和偏差

当测量数据是待估参数的非线性函数，由于非线性问题往往只有迭代解 (没有解析解)，估计的性质与线性模型有本质的不一样。

考虑如下一元非线性模型 (18)的参数估计的偏差和方差:

对于模型 (10)，为了得到其估计的性质，假设:(i)f(t，β)关于参数β存在一阶连续导数，且:

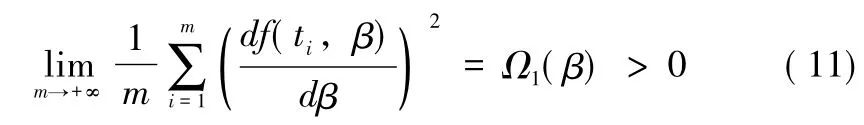
(ii)f(t，β)关于参数β存在二阶连续导数，且:

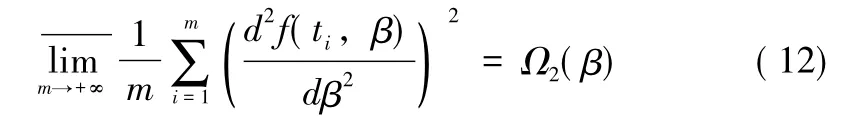
条件 (i)、(ii)自然而又必要的，因为在假设 (10)下，观测向量关于参数的 Fisher信息阵为因此，就表示观测中平均每个样本所包含的有关参数的Fisher信息。对于模型 (10)，我们有如下结论:

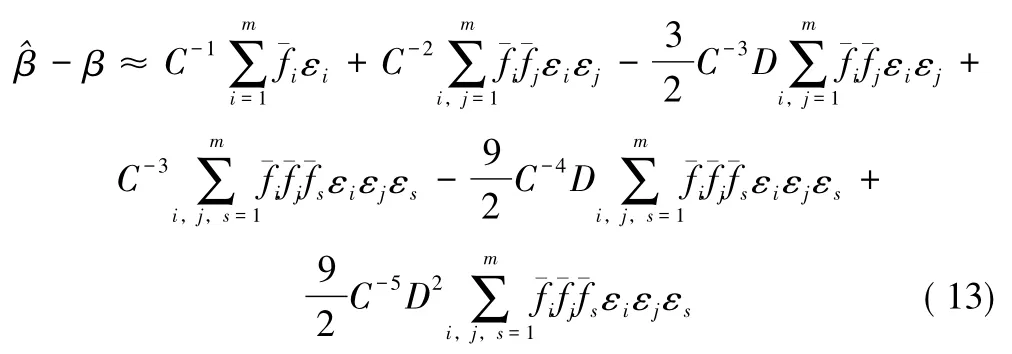
则参数估计的偏差和均方误差就有如下所示近似:

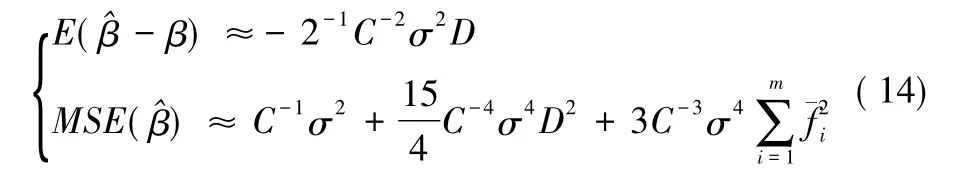
由定理2可知，非线性模型的参数估计是有偏的，其偏差和方差的值不但与测量数据的精度有关，而且同模型的一、二阶导数 (即模型的结构)有关，则与模型曲率也有关系［2-3］。模型曲率可等价于函数的非线性程度，故降低模型曲率可以降低函数非线性程度，从而有效地改善非线性模型的参数估计效果。

2.2 一元非线性融合模型的最优权值和参数估计

为了方便讨论，我们先只探究非线性回归模型:

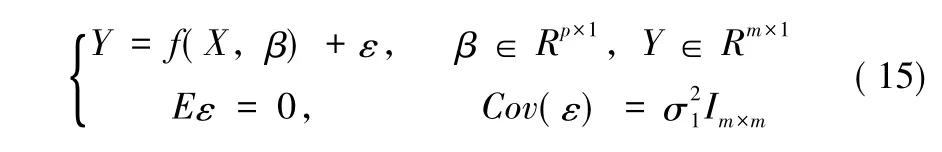
在线性约束模型 (2)(事实上，模型 (2)不仅可以当作先验信息，也可以当作另一类系统的测量数据)下的参数估计。根本上，两类系统的测量数据融合的最优权值问题，在参数估计均方误差最小的准则下，归结为寻找ρ，使得极小值问题:

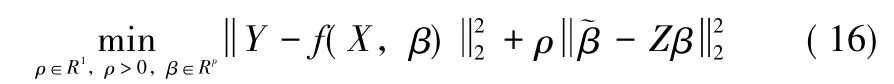
的解满足MSE(β^)(ρ)=E||(β^)(ρ)－ β||2=min［25］。

对于一元非线性模型，定理3提出了参数估计的偏差与均方误差，定理4提出了最优权值的存在性及其性质。

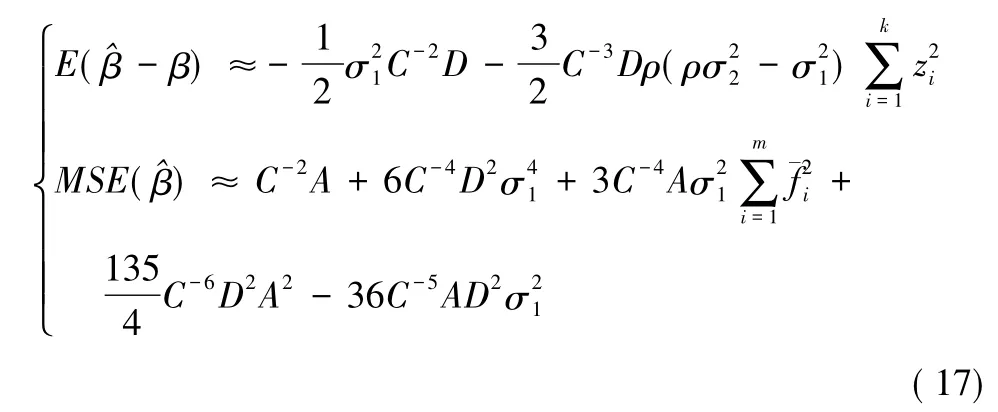
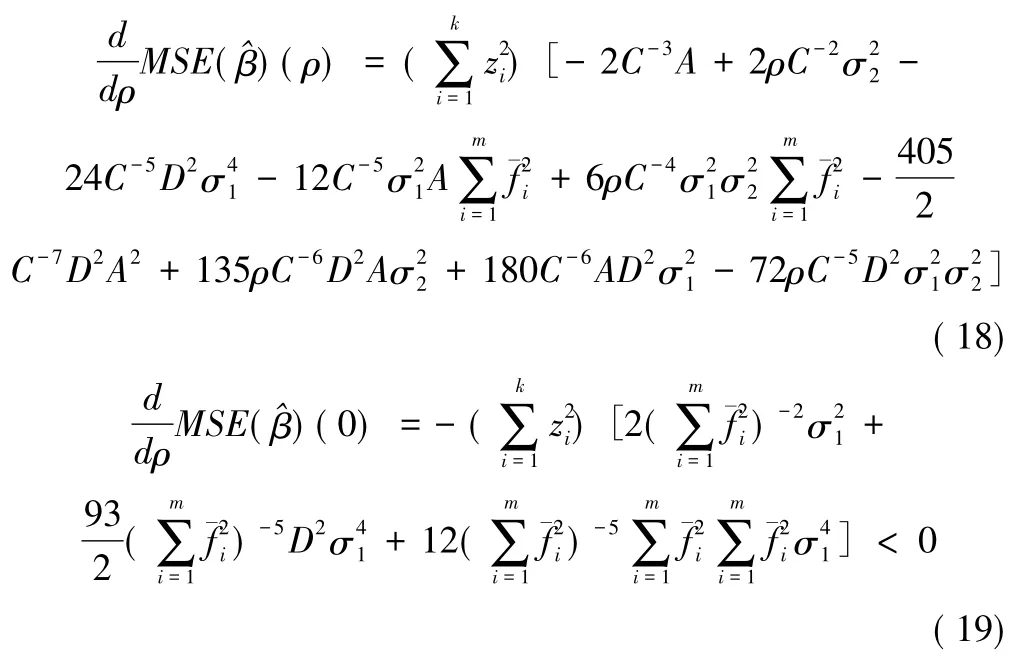
当ρ→+∞时，由第三项起始，之后的每项都是前两项的高阶无穷小量，又当时，前面两项之的和大于零，故存在ρ0＞0，使当＞0，因而

因此对于极小值问题 (16)的求解，我们按如下的迭代方式，确定多结构不同类型非线性测量数据融合的最优权值及相应的参数估计，算法步骤如下:

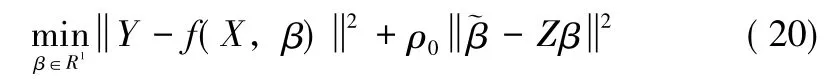
步骤2:由 (17)中的第二式，计算参数估计的均方误差在处的值

步骤4:将ρ1赋值给ρ0，重复步骤1，根据给定的收敛准则，重复上述四个步骤，一直迭代至收敛，此时的ρ1为最优融合权值，为参数的最优估计。

2.3 多结构多元非线性融合模型的最优权值与参数估计

根据如下所示的多结构多元非线性融合模型:

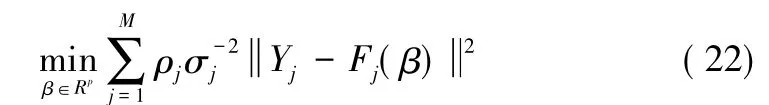
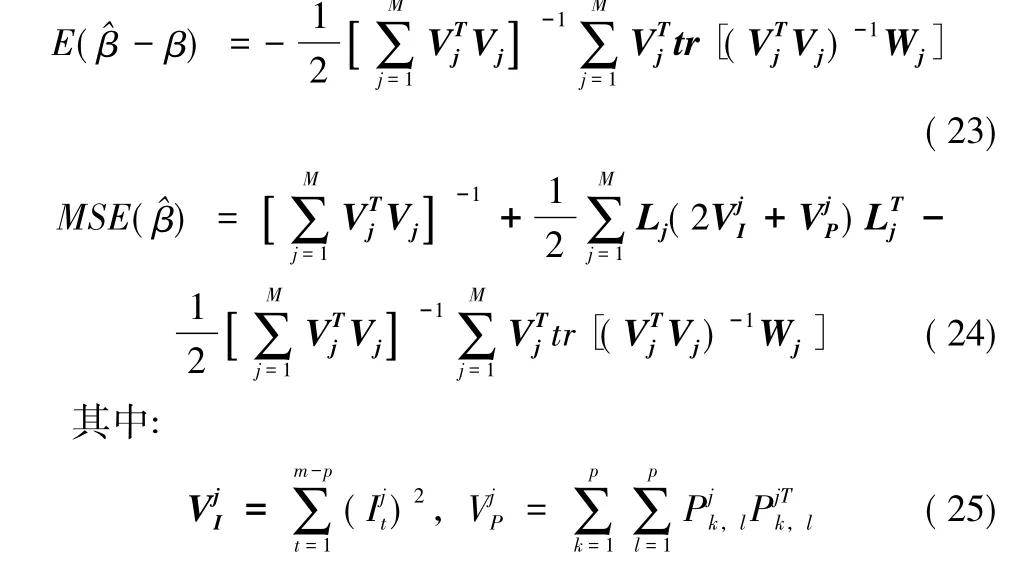
Vj=是上三角矩阵，的列向量是标准正交基。

定理5的证明过程类似于定理3和定理4，但此时由于参数是多维的，涉及到多元非线性函数的模型曲率求解，具体证明方法可参考文献［6］。

步骤1:对于给定的一组权值 ρ(0)，设定迭代初值β(0)，使用观测数据关于待估参数的函数式获得到Fj(β(0));

步骤2:记ei为第i个分量为1，其他分量全为0的向量，根据设定数值微分的步长h(根据实际情况，一般可设定为h=10－6)，计算Fj(β(0))梯度矩阵:

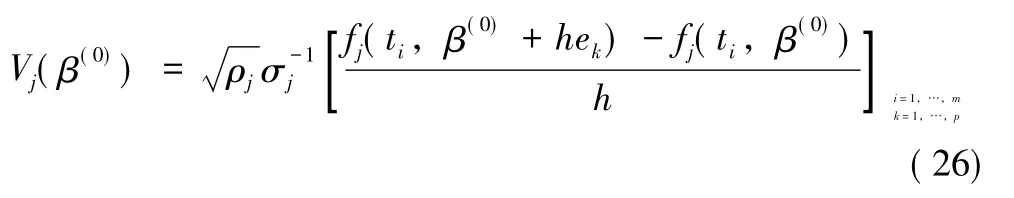
并对此进行QR分解，得到矩阵Lj(β(0));

步骤3:由下式得到参数β的一次改进:

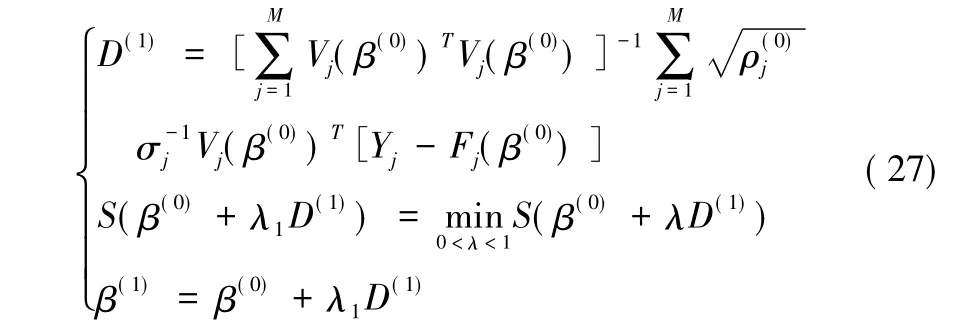
步骤4:对于给定的收敛阈值τ＞0，如果|S(β(1))－S(β(0))|＜τ，则迭代结束，令转入Step5;否则，令β(0)=β(1)，返回Step1;

3 算例验证

算例1:设某物理量u真值为10，有不等精度的两套设备对其进行直接测量，分别得到100个高精度的观测数据 (均方根差为1)，180个低精度的观测数据 (均方根差为4)，共产生100组观测数据，得到的参数u的估计及方差见表1。(估计的根方差是对100组观测数据统计得到。)

表1 四种估计的比较

在线性观测数据融合处理时，唯一的最优融合权值由测量数据的精度决定;求解极小值问题 (8)100次，得到均方误差为0.061，估计是最优的。

算例2(一元非线性融合模型的最优权值与参数估计):

设 f(tj，β) = 1+(5+tjβ)0．1，y(tj) = f(tj，β)+ε(tj)，ε(tj)i～idN(0，0．052)，z(si)=β+η(si)，η(si)i．～i．dN(0，0.012)，令tj=0．05 × (j－ 1)，j=1，…，300，si=2+0．1×(i－1)，i=1，…，100，β的真值为8，产生50组观测数据计算结果见表2，均方误差与加权因子关系见图1。

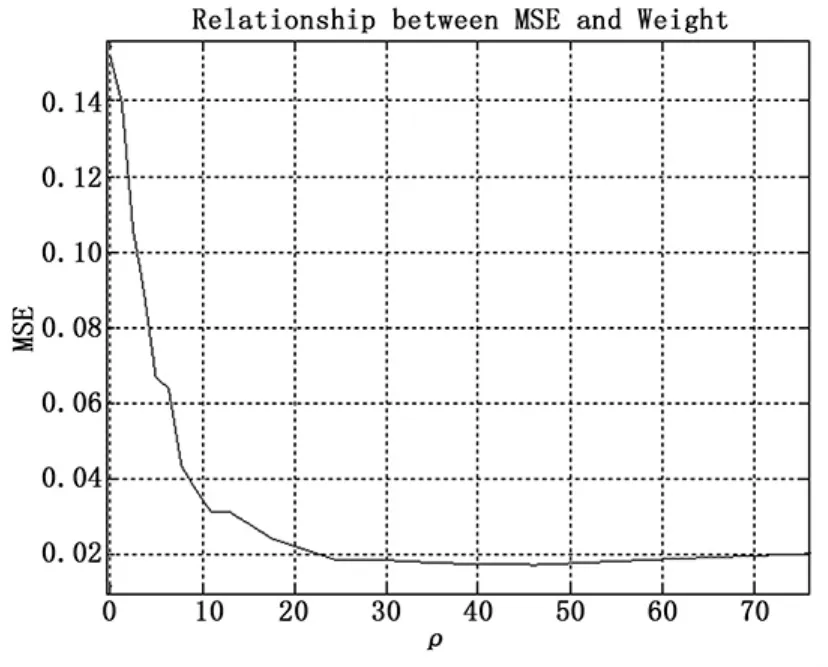
图1 均方误差和加权因子关系图

当采用线性模型的加权方式，即取权值ρ=0.052/0.012时，得到均方误差为0.020;而当ρ=1．80×0.052/0．012时，参数估计的均方误差得到最小，其值为0.017。

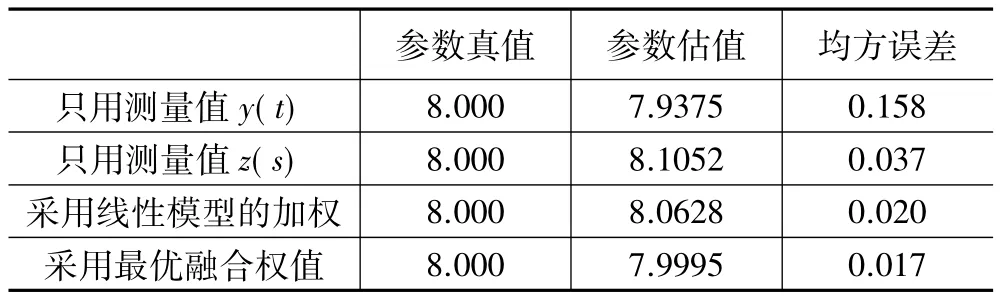
表2 各种加权的参数估计结果对比

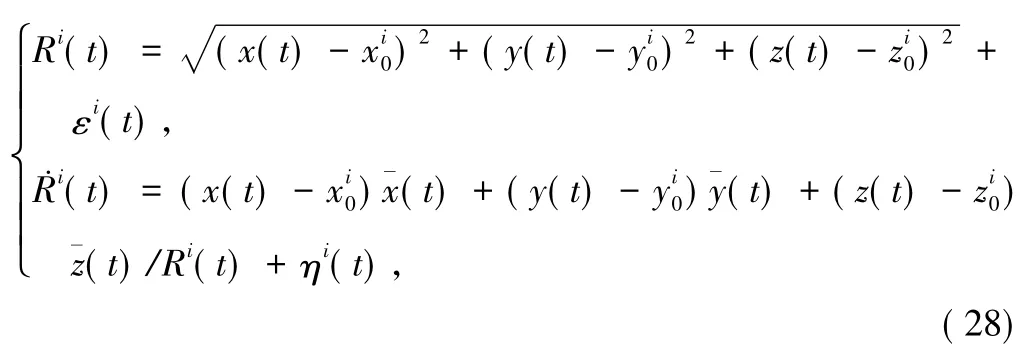
算例3(弹道目标跟踪)。

以连续波雷达和自主外测设备构建多测距测速弹道目标跟踪系统，假设有3个测量站，分别测量弹道目标的距离R和速度R，测量值可以表达为:

假设各观测量测量误差服从高斯分布，且各观测站的观测量互不相关，满足独立同分布条件:

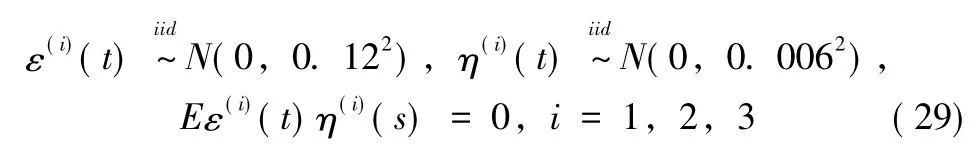
仿真参数设置如下:各观测量的采样率为20 Hz，即t=0．05×j，j=1，…，600， 各测量站的站址坐标为，i=1，2，3，弹道目标在t时刻的状态矢量可表示为利用理论弹道带入公式(28)生成由弹道目标的距离R和速度组成的观测数据本例采用文献 ［4］提出的节省参数建模方法，利用不等间距最优节点的三次样条函数对弹道进行建模，采用最小二乘法对该非线性回归模型的样条系数和弹道参数进行估计，ρ为最优权值，仿真次数为100次。

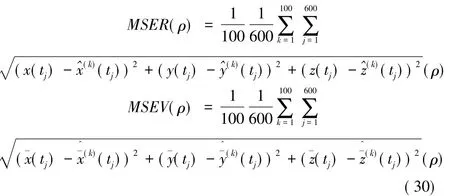
仿真结果表明:当ρ=0．122/0．0062时，MSER(ρ)=0.322 m，MSEV(ρ)=0.049 3 m/s; 当 ρ = 2．33 ×0.122/0.0062时，MSER(ρ)，MSEV(ρ)达到最小值，其值分别为0.082 m，0.029 4 m/s。可以看出，多结构多元非线性融合模型可以有效提高弹道目标的估计精度。

算例4(多测速联合定轨)

依靠同一时刻的N个(N≥6)以上的测速元，可以确定该时刻的轨道参数 X(t)。以(xk，yk，zk)，(k=1，2，．．，N)为N个互不相同的测站在相同坐标系下的站址坐标，N个测速可表示为:

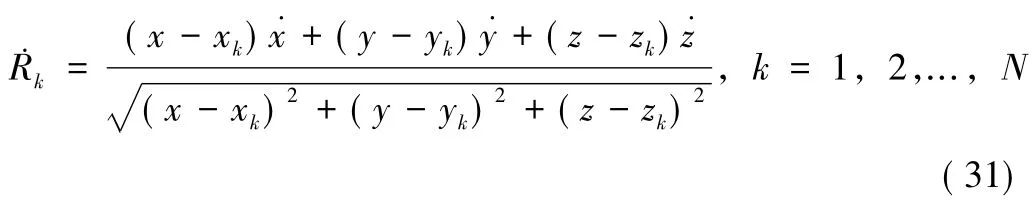
上式就是联系测速元与目标位置和目标速度的测量方程。对于是 N个互不相同的站址，Jacobi(雅克比)矩阵为:

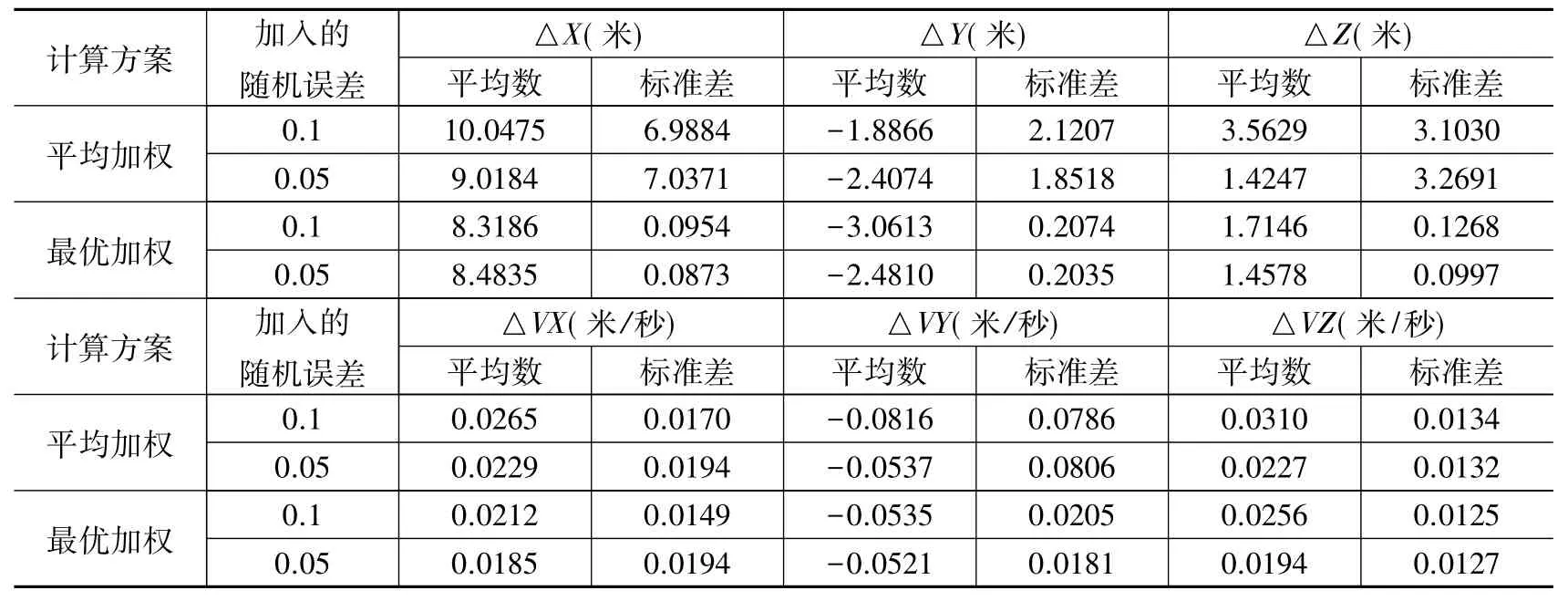
表3 测速定轨结果与基准轨道作差统计表

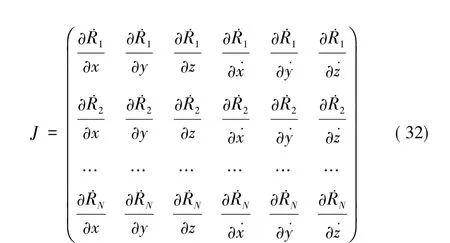
若雅克比矩阵是列满秩矩阵，从而由反函数存在定理，可以有由式(1)唯一地确定轨道参数:

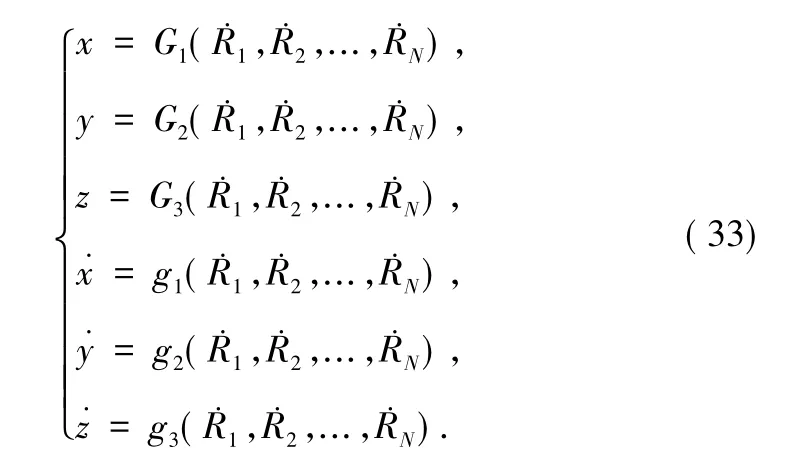
假设各观测量测量误差服从高斯分布，且各观测站的观测量互不相关，满足独立同分布条件:

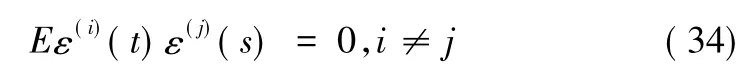
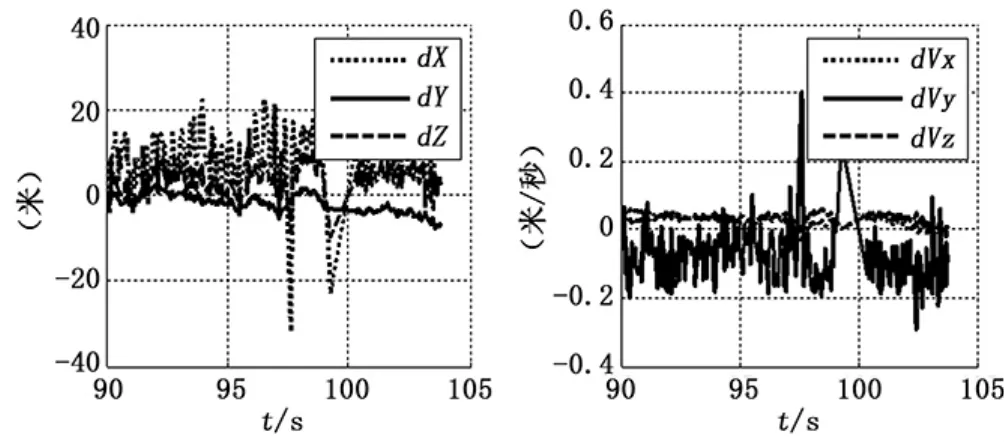
图2 平均加权定轨结果与基准弹道减法统计图(0.1 m/s的随机误差，左图为位置，右图为速度)

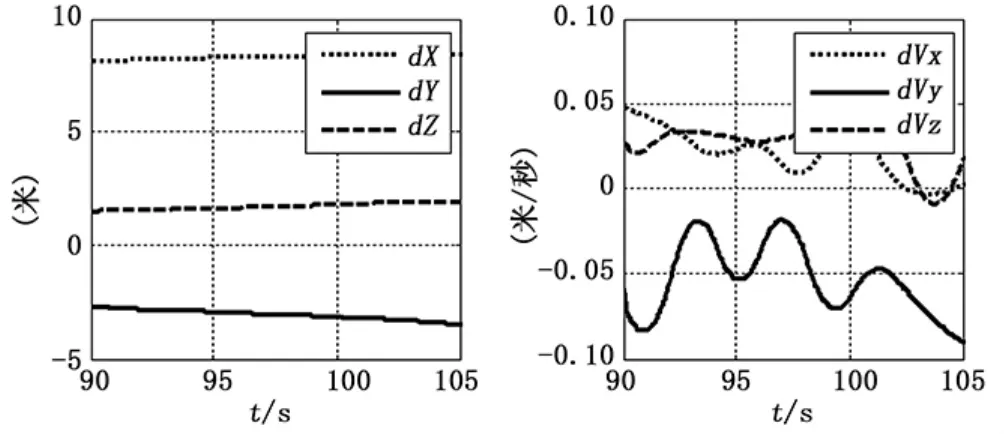
图3 最优加权定轨结果与基准轨道减法统计图(0.1 m/s的随机误差，左图为位置，右图为速度)

图2和图3分别为加0.1 m/s的随机误差条件下平均加权和最优加权定轨结果与基准弹道作差统计结果，由图可知平均加权方式的差值波动较大，而最优加权方式的波动较小。此外，从表中3均值和标准差的统计结论可以看出，采用非线性回归模型最优融合估计方式进行多测速定轨可以不同测速元测量精度差异对定轨精度的影响，精度高于平均估计加权方式，满足靶场试验高精度测量系统定轨应用需求。

4 结论

测量数据的融合处理是提高数据处理精度的有效措施。本文研究了不等精度观测数据融合的权值和参数估计问题。对于线性融合模型，其最优权值由测量数据的精度唯一确定，这与经典的Gauss－Markov定理是一致的;而对于非线性融合模型，通过参数估计的均方误差的曲率矩阵表达，建立了多结构不等精度非线性回归模型的最优加权理论与算法，并给出了计算实例，结果表明:多结构非线性回归模型的加权数值会对参数估计精度产生非常大的影响，其最优权值不仅仅和其他各类数据的测量误差统计特性相关联，还与各类数据模型的结构，即模型曲率、样本量的大小等有关，从而由线性模型Gauss－Markov定理得到权值(仅与观测数据精度有关)不再是最优的。