汽车荷载与河水耦合作用下公路边坡应力应变分析

蒋琳琳，张炅冏，赵 川

(1.天津大学仁爱学院，天津301636；2.水利部海委海河下游管理局，天津300061；3.四川君信工程项目管理咨询有限公司，四川成都610091)

0 引 言

我国山地分布广泛，工程地质水文地质条件十分复杂，不可避免地出现了大量涉河的公路边坡，而河水流量受季节影响很大，河水高程不断发生变化，对两岸高陡山体上建设的公路边坡稳定性产生了极大影响。因此，研究汽车荷载与河水位变化耦合作用条件下的公路岩质边坡稳定性具有十分重要的现实意义[1- 3]。郑颖人等[4]利用非稳定渗流微分方程推导出了库水位下降时坡体内浸润线的计算公式，并研究了水位下降高度对土质边坡安全系数的影响；崔洁[5]采用SLOPE/W软件，计算某水电站水库右岸边坡在不同水位升降速度情况下边坡的安全系数变化规律发现，水位上升速率越快，边坡越趋于稳定；王世梅[6]等以谭家河滑坡为研究对象，分析了不同库水位升降速率对滑坡渗流场和稳定性的影响，得到了不同库水位升降速率与边坡地下水位线和稳定性之间的规律。

通过对已有的涉水边坡稳定性相关文献的调研和分析发现[7- 10]，对于水位升降条件下边坡稳定的研究已日趋成熟，而对于荷载和河水位变化耦合作用下的公路岩质边坡稳定性的有关研究还很少，且尚未形成统一结论。为此，本文结合一典型的涉河顺层岩石公路边坡工程实例，基于有限元渗流基本理论，采用有限元软件PLAXIS[11]，研究分析该公路边坡在考虑瞬时汽车荷载和河水位下降过程中的应力应变特征，进一步揭示该类岩质边坡稳定性的变化趋势。

1 工程概况

本文研究的涉河公路边坡地貌属低山峡谷区，山峦叠嶂，峰高谷深，山脉多呈南北或北东走向，与构造线展布方向大体一致，属于典型的顺层高陡岩质边坡。该公路边坡研究区覆盖层为第四系全新统填筑土、坡残积碎石土，下伏基岩为奥陶系下统湄潭组地层。涉河公路高陡边坡见图1。地层岩性分述如下：

图1 涉河公路高陡边坡

(1)第四系全新统填筑土。主要由碎石、角砾、粉土，碎石含量约51%～62%，土石工程分级为Ⅱ类土，属普通土。

(2)奥陶系下统湄潭组。岩性为灰岩，灰色，细晶结构，中厚层状构造，主要成分方解石等，钙质胶结。按风化程度划分为：①强风化层：岩石裂隙发育，裂面可见黄褐色氧化铁薄膜或斑点，厚3.3～8.2 m。②中风化层：岩石裂隙一般不发育，最大揭露厚度40.30 m(未揭穿)。岩石承载力基本容许值为400～1 200 kPa，土石工程分级为V级，属次坚石。根据工程地质勘查报告，获取了该涉河公路边坡各岩层力学参数建议值，见表1。由于边坡表面土层相对较薄，且不是边坡整体稳定的控制性因素，因此本次计算暂不考虑覆盖层的影响。材料模型采用摩尔-库伦屈服模型。

表1 各岩层力学参数建议值

2 模型建立

本次公路边坡的稳定计算主要采用荷兰PLAXIS B.V.公司推出的有限元软件PLAXIS[12]中的渗流模块和边坡稳定计算模块。

根据相关资料，并结合数值计算的有关需求，对实际涉河公路边坡进行一定程度的简化处理，最终建立的边坡有限元模型长545 m，高380 m，汽车荷载取200 kN，计算模型见图2。图3为水面高程600 m时对应的边坡渗流云图，反应了不同部位的渗流速度分布。根据水文资料得知，该河常年最高水面高程600 m，最低枯水期水面高程550 m，本次稳定计算范围主要选取河水面高程从600 m降至550 m，10 m为1个计算梯度，降低速率按1 m/d进行控制，总的计算时间为50 d。由于该河不会出现水位骤降工况，因此渗流计算采用稳态渗流模型，即坡体内浸润线随水位下降而下降。

图2 公路边坡有限元计算模型

图3 公路边坡有限元渗流速度云图(mm/d)

3 计算结果分析

3.1 应力应变分析

剪应变反应的是岩体受力产生变形时内部各点的变形程度，可以用来描述一点处变形程度的力学量。图4为同时考虑了瞬时车荷载的作用，水面高程从600 m逐渐降低至550 m过程中边坡岩体内的剪应变分布。从图4可知，随着水位的逐渐降低，坡体最大剪应变逐渐增大；在水面高程从600 m降至580 m期间(降水初期)，最大剪应变主要分布在深部基岩内，而公路涉水边坡表面分布相对不明显；而当水面高程从580 m降至550 m期间(降水后期)，深部基岩内的最大剪应变逐渐消失，最大剪应变主要分布在中风化层和基岩交界面以及公路边坡平台下部的陡坡表层，即强风化岩层，最大值约50×10-3%～60×10-3%。说明公路涉水边坡剪应变分布受降水前期影响较小，受降水后期的影响相对较大。

图4 水位下降过程中边坡岩体剪应变(10-3%)

由于岩体材料模型遵循摩尔-库仑(M-C)屈服准则，摩尔-库仑(M-C)准则是考虑了正应力或平均应力作用的最大剪应力屈服理论，即当剪切面上的剪应力与正应力之比达到最大时，材料发生屈服破坏。因此，本文采用摩尔-库仑塑性点来反应该边坡岩体的塑性变形趋势，水位下降过程中边坡岩体塑性区见图5。从图5可知，当水面高程从600 m降至580 m期间，边坡强风化和中风化岩体内塑性区范围逐渐减少(由于新鲜基岩位置较深，不需对深部新鲜基岩进行分析)；水位降低至580 m时，坡面塑性区主要分布在中风化层和基岩交界面，其余少量塑性点分布在公路边坡平台上部和下部岩体；而随着水位的进一步下降，从580 m降至550 m时，公路边坡平台上部岩体的塑性区范围又逐渐扩大，这是由于公路平台下部水位降低，造成孔隙水压力逐渐消散，汽车荷载的有效应力逐渐增大的原因。

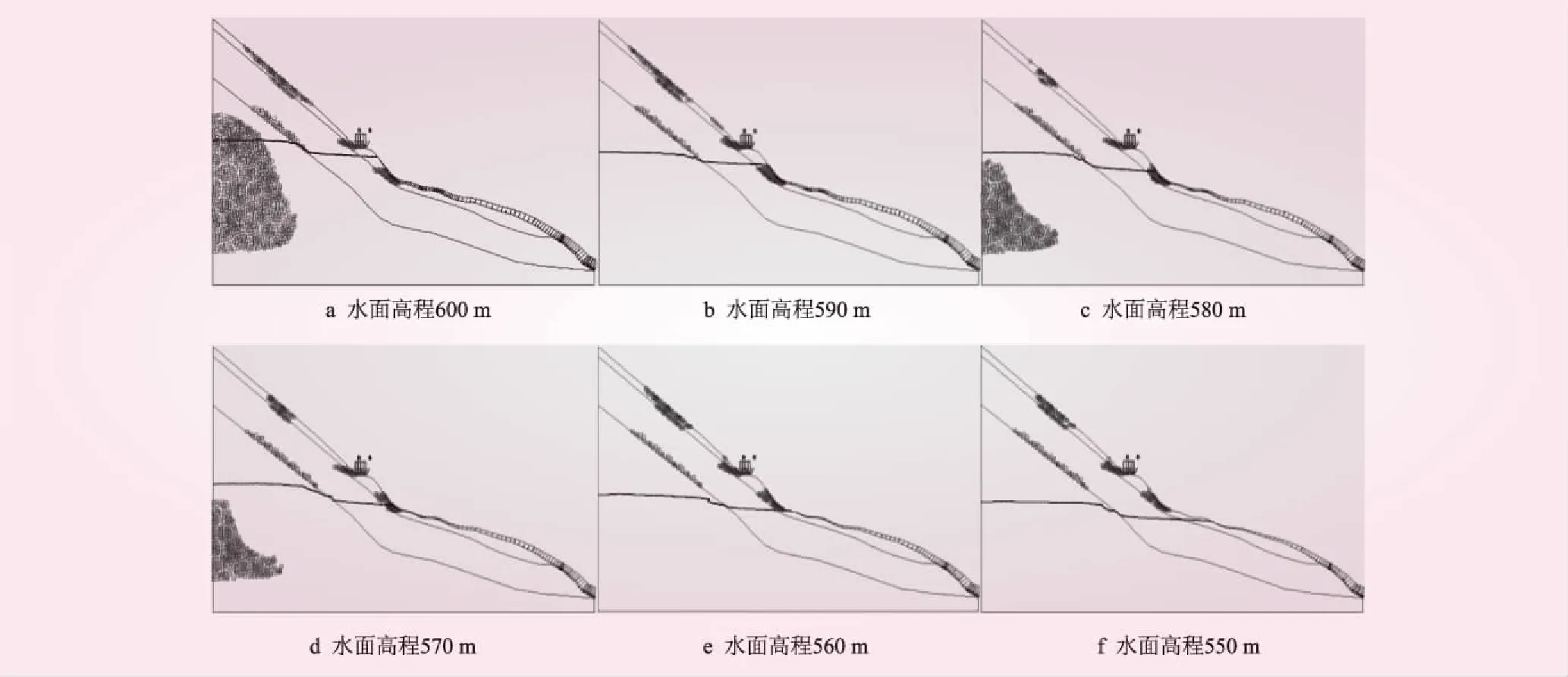
图5 水位下降过程中边坡岩体塑性区

图6 水位下降过程中边坡滑裂面分布

3.2 稳定分析

为研究水位下降过程中公路边坡的稳定性变化趋势，采用有限元强度折减法计算得到了水位下降过程中边坡的安全系数，见表2。从表2可知，在初始阶段最高水面高程为600 m时，边坡稳定安全系数为1.307；水面高程从600 m降至580 m过程中，安全系数逐渐增大，其中当水面高程在580 m时边坡的安全系数最大为1.38；之后水面高程从580 m降至550 m时，安全系数又开始逐渐减小，最终在最低水面高程为550 m时边坡稳定安全系数为1.321。这与上文中边坡塑性区的变化趋势分析结果一致，但与以往认为的水位下降时边坡稳定性也会下降的结论不完全相同。

图6为水位下降过程中公路边坡的最不利滑裂面分布。从图6可知，各水位对应的滑裂面基本相同，均起于边坡顶部，滑弧中部与中风化层和新鲜基岩的交界面相切，从公路平台下部陡坡坡脚处剪出。图7为水位下降过程中公路平台岩体最大位移。从图7可知，随着河水位的逐渐下降，公路平台产生的位移逐渐增大，水面高程从600 m降至580 m过程中，最大位移从23 mm增大至53 mm；而当水面高程从580 m降至550 m过程中，最大位移仅从53 mm增大到57 mm，仅增大了4 mm，说明降水前期公路边坡平台变形较大，而降水后期变形不明显，可以忽略。

表2 边坡稳定安全系数

图7 公路平台最大位移

4 结 语

本文基于有限元渗流基本理论，采用有限元软件PLAXIS计算分析了某涉河的顺层岩质公路边坡在考虑汽车荷载和河水位下降过程中的应力应变特征及稳定性变化情况，得到以下结论：

(1)该公路涉水边坡坡面剪应变的分布范围受前期降水影响较小，受后期降水的影响相对较大。后期降水阶段最大剪应变分布在中风化层和基岩交界面以及公路边坡平台下部的陡坡强风化岩层内。

(2)随着河水位的逐渐降低，岩质边坡表层的塑性区分布范围呈现先减小后增大的变化趋势，当水面高程为580 m时，坡面塑性区范围最小，仅少量分布在公路边坡平台上部和下部岩体。

(3)随着河水位的逐渐降低，该公路边坡稳定安全系数呈现先增大后减小的变化趋势，当水位高程为580 m时边坡的安全系数最大为1.38，最低水位时为1.321，高于最高水位对应的安全系数。各水位对应的最不利滑裂面基本相同，剪出口均位于公路平台下部陡坡坡脚处。

(4)随着河水位逐渐下降，公路平台产生的位移逐渐增大。前期降水阶段，公路边坡平台变形较大，位移增大明显，而后期降水期间的变形很小，可以不予考虑。