高强钢组合Y形偏心支撑钢框架抗震性能与震后修复分析

段留省，苏明周，李 慧

( 1. 长安大学 建筑工程学院，陕西 西安 710061；2. 西安建筑科技大学 土木工程学院，陕西 西安 710055；3. 恒大地产集团西安有限公司，陕西 西安 710000)

高强钢组合Y形偏心支撑钢框架(HEY)是一种新型结构体系[1]，其耗能梁段采用屈服点较低钢材并通过弹塑性变形耗散地震能量；框架与支撑采用高强度钢材，为耗能梁段提供足够的约束，减少用钢量，剪切屈服型试件的耗能能力和承载力高于弯曲屈服型试件，这与普通Y形偏心支撑钢框架的研究成果基本一致[2-3].1/2缩尺3层Y形偏心支撑钢框架振动台试验和拟静力试验表明表明试件抗震性能良好，但耗能梁段下端出现平面外变形[4-5].Montuori等对Y形偏心支撑钢框架进行刚塑性理论分析，提出相应设计方法[6-7].Y形偏心支撑可用于RC框架震后加固，加固后结构的承载力、抗侧刚度和耗能能力均有提高[8-9].有限元分析结果表明加固后RC框架的耗能能力显著提高，框架震害有所减轻[10].Shayanfar等对Y形偏心支撑钢框架普通型钢耗能梁段和型钢混凝土组合耗能梁段进行研究，表明后者受剪承载力和延性较好[11].段留省等对1榀单层单跨1/2缩尺的高强钢组合K形偏心支撑钢框架进行震后修复试验，表明修复后的极限承载力与原试件相当，延性系数略有降低[12].纪晓东等对可更换钢连梁抗震性能和震后更换可行性进行试验研究，转角达到0.02rad时更换连梁，采用耗费时间和残余转角评定可更换能力[13-14].超短连梁循环加载试验表明连梁的弹塑性转角接近0.14rad，采用LYP225钢时转角增大25%，翼缘的抗剪作用和腹板应变硬化对连梁的超强系数影响较大[15].

为进一步研究HEY试件的抗震性能和震后修复可行性，在试验的基础上采用ANSYS软件对一组HEY试件进行有限元分析，考虑材料非线性和几何非线性，重点研究受力性能、破坏机制、塑性转动能力.

1 有限元模型

1.1 几何模型与网格划分

为便于验证，有限元模型YL的尺寸与文献[1]中试件HEYS一致，仅改变耗能梁段长度，以研究HEY试件的抗震性能和耗能机制.试件尺寸见图1，耗能梁段截面见表1，其中e为耗能梁段长度，H为框架的层高.

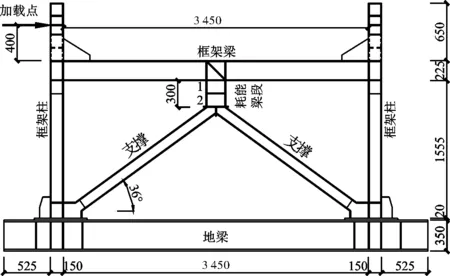
图1 HEYS试件立面图(单位：mm)Fig.1 Elevation of HEYS specimens(unit: mm)

试件e/mme/H耗能梁段截面钢材牌号YL13001/6YL24001/4.5YL35001/3.6H225×125×6×10Q345B

有限元模型及边界条件见图2(a)，网格划分采用实体单元，耗能梁段和柱脚底板分别采用Solid186和Solid187单元，其他构件均采用Soild185单元.耦合加载点标高处节点的X方向位移ux，以模拟加载梁[1]，框架梁的面外支撑通过约束该处节点的Y方向位移uy实现；固接柱脚通过约束底板底面节点的全部自由度实现.

有限元中材料的本构关系采用多线性随动强化模型[16]，其中考虑Bauchinger效应，见图2(b).材料性能见表2.

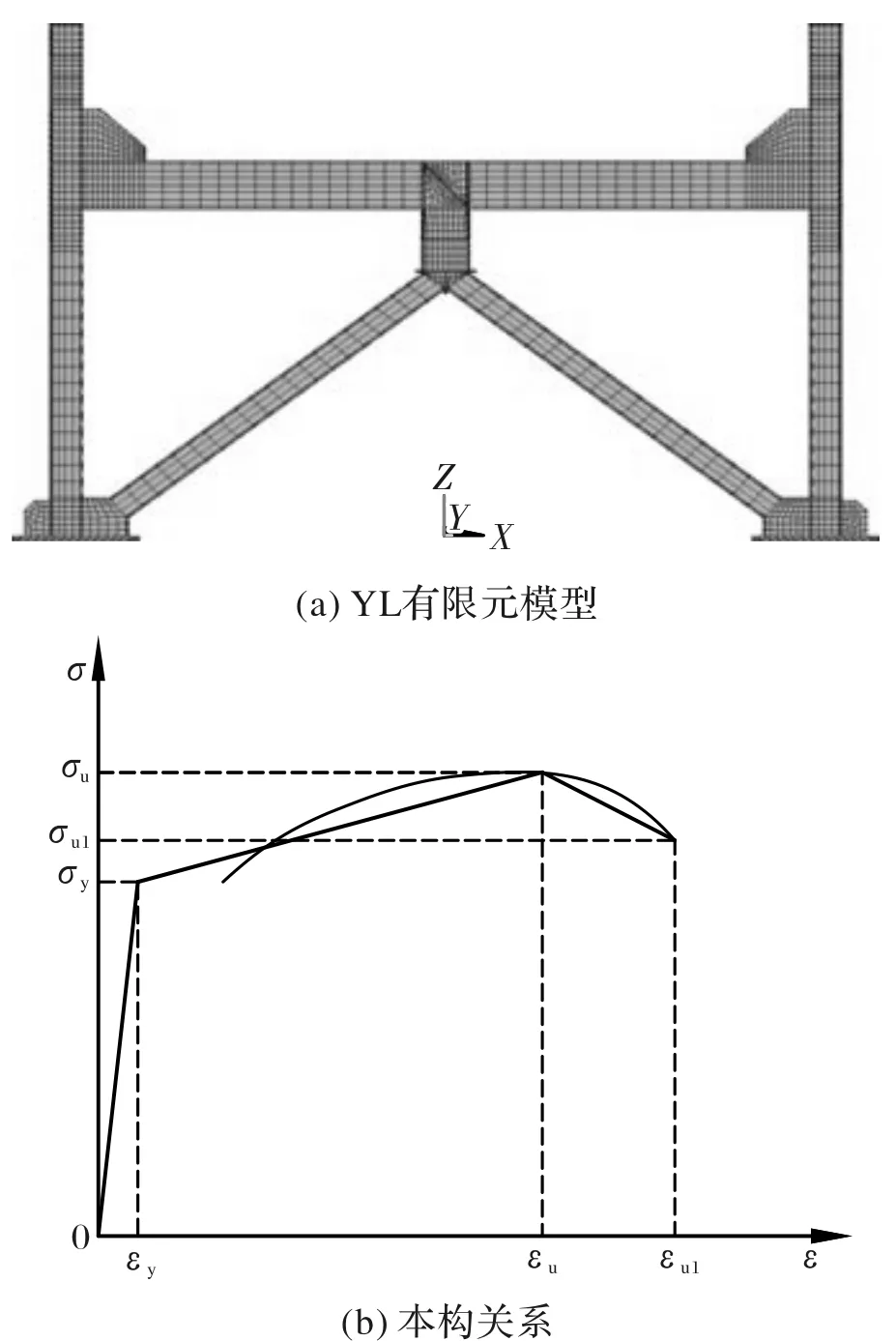
图2 有限元模型与本构关系Fig.2 FEM specimens and constitutive model

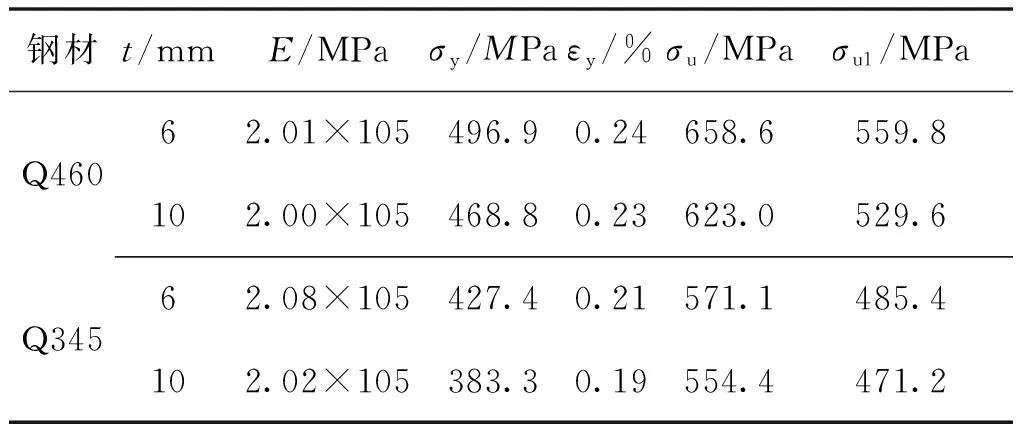
钢材t/mmE/MPaσy/MPaεy/%σu/MPaσu1/MPaQ46062.01×105496.90.24658.6559.8102.00×105468.80.23623.0529.6Q34562.08×105427.40.21571.1485.4102.02×105383.30.19554.4471.2

1.2 加载制度和破坏准则

为消除加载制度对试件耗能能力的影响，加载时采用相同的加载制度，循环加载制度见表3.其中N为循环圈数，δy为估算屈服位移，取10 mm.

为便于分析，在有限元模型未计入构件的初始几何缺陷以及残余应力，试件发生下列情况之一即认为破坏：1)耗能梁段最大Von mises应力超过材料的极限应力；2)层间位移角超过1/25；3)构件严重屈曲[17].

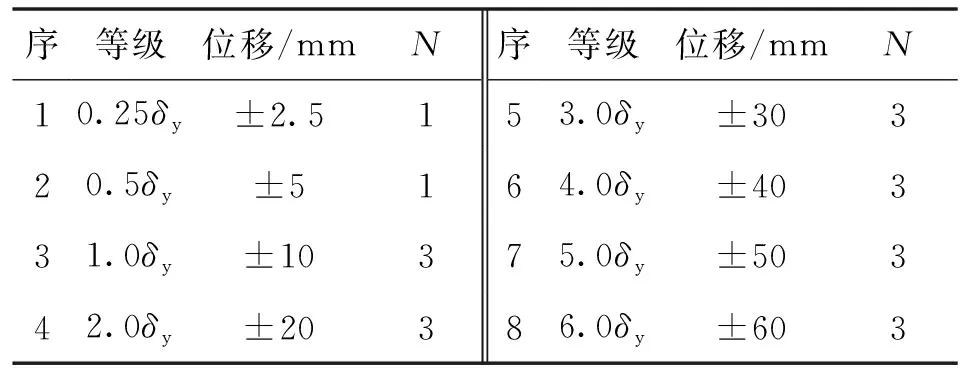
表3 循环加载制度[17]

2 结果分析

2.1 破坏现象与荷载-位移曲线

试件YL1、YL2、YL3循环加载的破坏形态见图3，由图可知，三者的耗能梁段发生明显弹塑性变形，其他构件变形较小.

试件YL1耗能梁段腹板的屈曲现象明显，翼缘有一定弯曲；YL2试件耗能梁段整个腹板均出现屈曲现象；YL3试件耗能梁段有明显倾斜现象，仅在靠近框架梁底的区格出现腹板屈曲，翼缘弯曲，其他区格变形较小.

各试件循环加载的滞回曲线(荷载P-位移Δ)见图4，由图可知，各曲线的滞回环稳定、饱满，无明显下降段；试件的初始刚度随着耗能梁段长度增大而减小，由于截面尺寸一致，三者的极限荷载相差不大.

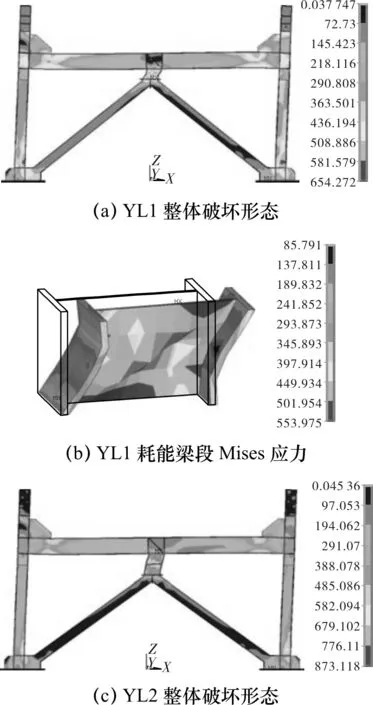
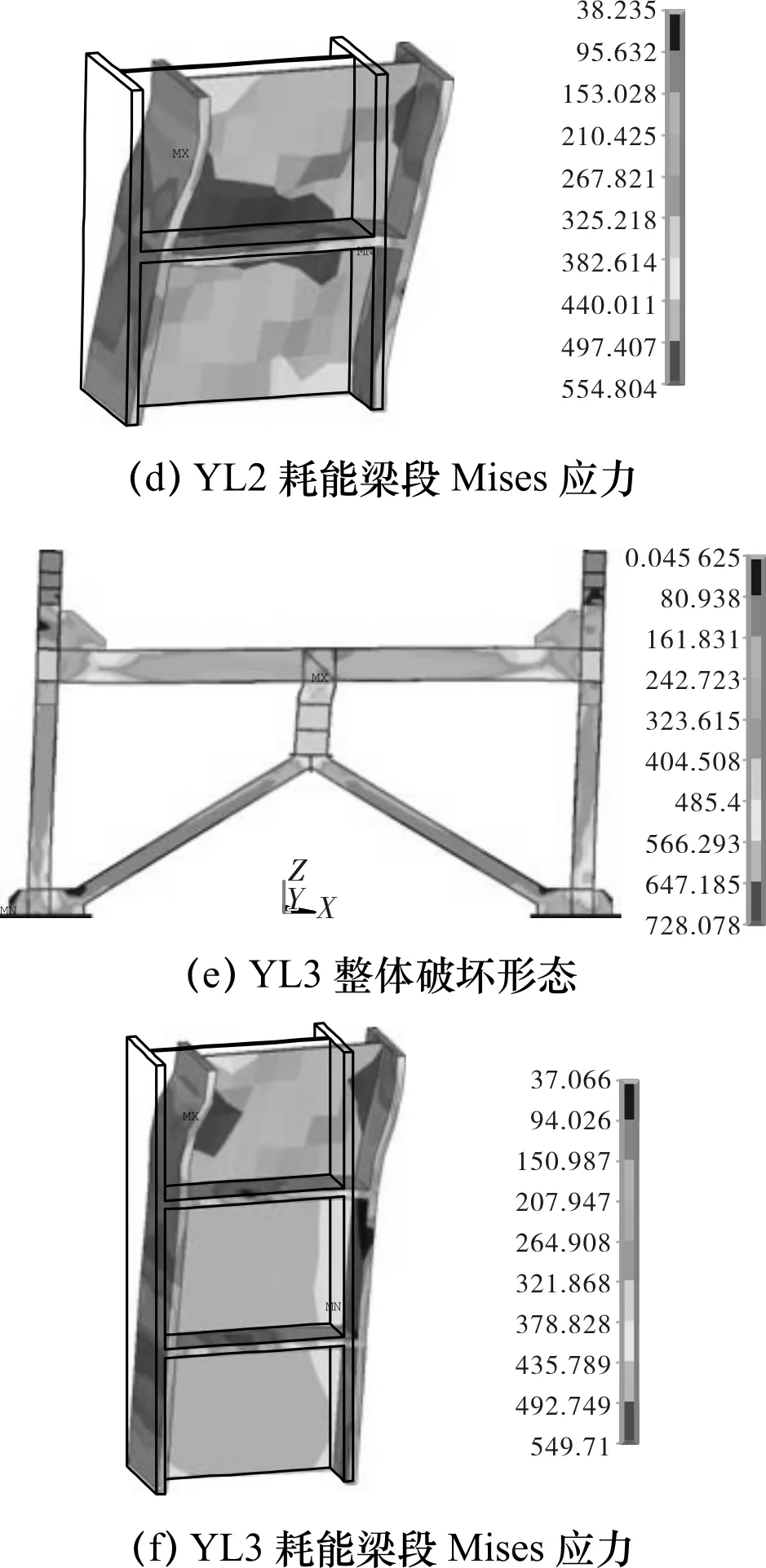
图3 循环加载破坏形态Fig.3 Failure modes of cyclic loading

图4 滞回曲线Fig.4 Load-displacement curves of cyclic loading

2.2 骨架曲线和刚度退化

循环荷载下的骨架曲线见图5，由图可知，试件YL1、YL2、YL3骨架曲线存在明显的线弹性段，有转折点，弹塑性变形段持续较长，无下降段.在0.02 rad层间位移角之前，YL1的荷载高于后二者，之后三者荷载差距逐渐减小，原因是耗能梁退出工作，抗侧刚度主要由框架提供.

三者的刚度退化曲线见图6，由图可知，三者刚度退化曲线趋势相似，刚度退化速率随着耗能梁段长度增大而减缓，在0.1 rad层间位移角之前，三者刚度退化较快；之后由于耗能梁段屈服，刚度退化速率减缓，YL1的剩余刚度最大，表明耗能梁段长度对刚度退化影响较大.

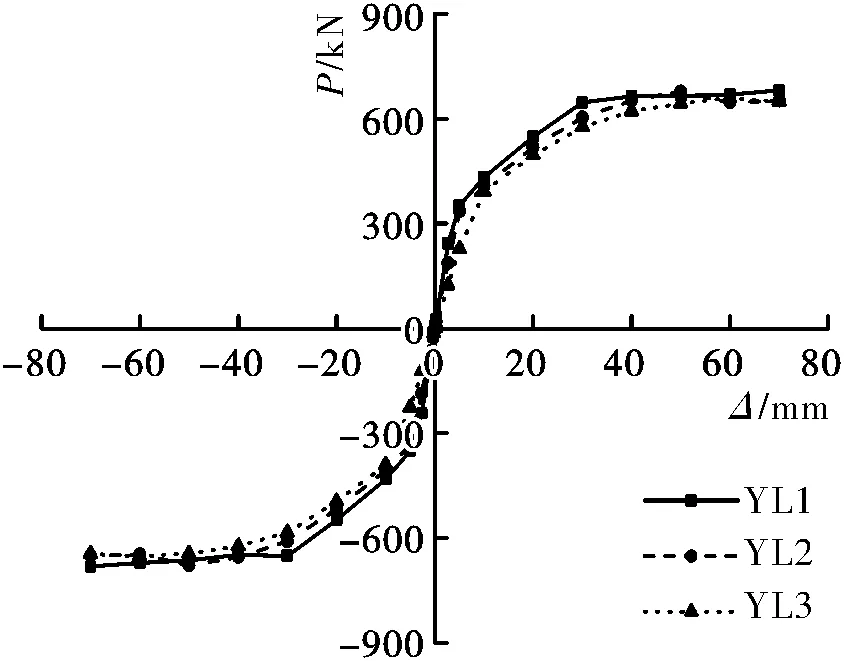
图5 骨架曲线Fig.5 Skeleton curves

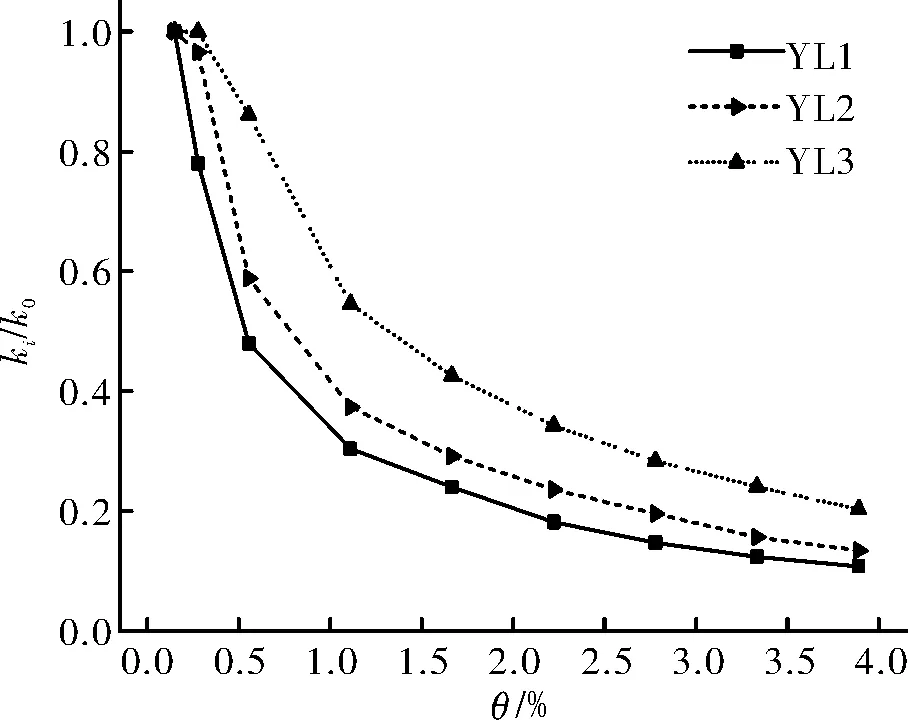
图6 刚度退化曲线Fig.6 Degeneration curves of rigidity

2.3 承载力与延性

P-Δ曲线分析结果见表4，由表可知，试件YL1、YL2和YL3的初始刚度随着耗能梁段长度增大而减小，YL1推(拉)方向的初始刚度比后二者分别高30.2%(29.6%)、98.1%(97.3).耗能梁段长度对试件的承载力影响不大，YL1推(拉)方向的极限荷载比YL2、YL3高0.6%(0.5%)、3.4%(4.6%)；延性系数随耗能梁段长度增大而降低.结构的延性用位移延性系数μ来评定[14]，即破坏位移Δu与屈服位移Δy的比值.结构的变形能力用层间位移角θ(θ=Δ/H，H为层高)来评定.结构的屈服位移Δy采用等效弹性刚度法[15]，确定见图7；荷载下降到极限承载力的85%的点作为破坏点，其位移破坏位移Δu.

2.4 耗能能力

以耗散能量E和等效粘滞阻尼系数he评定试件的耗能能力，各试件的耗能能力分析见表5.由表可知，试件YL1、YL2和YL3的等效粘滞阻尼系数在0.02 rad位移角之前差别较大，YL1的耗能梁段长度最短，弹塑性变形发生最早，he增长最快；0.02 rad之后，由于梁段屈曲，抗侧刚度主要由钢框架提供，he增长速度减缓，三者差异减小.

YL1、YL2和YL3试件的耗散能量对比见图8，由图可知，随着位移增大，三者的耗散能量都迅速增大，在1/50层间位移角之前，耗能梁段越短，耗散能量越多；1/50之后，三者相差很小.

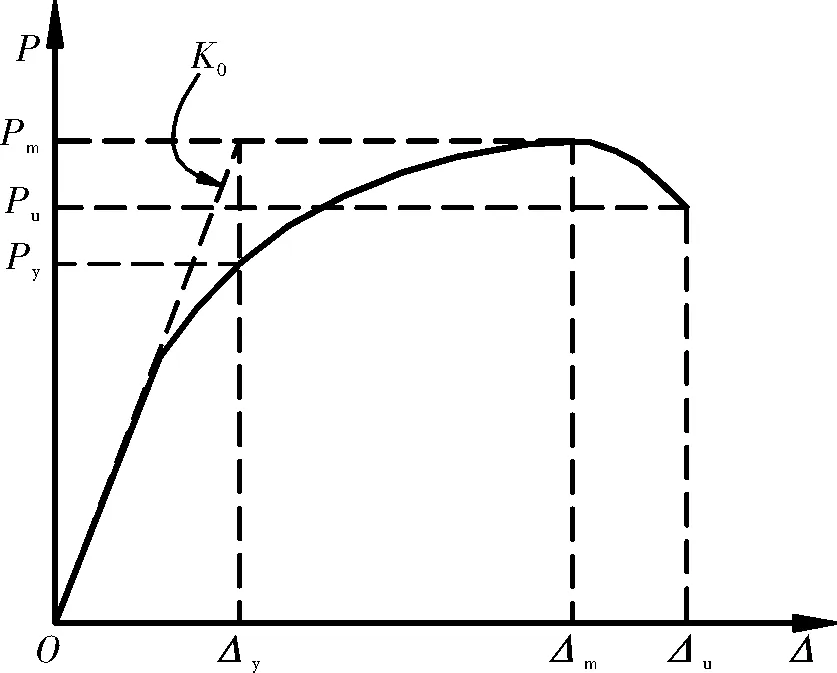
图7 确定结构屈服点Fig.7 Estimation of structure yield point

图8 耗散能量对比Fig.8 Comparison of energy dissipation capacity

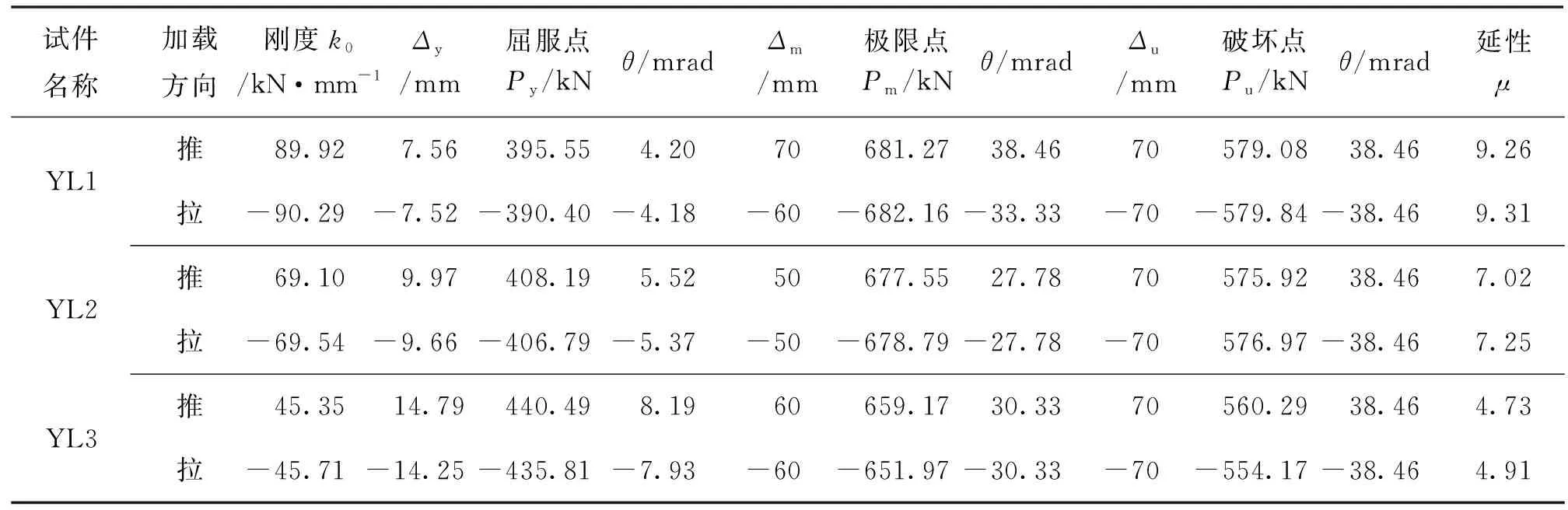
试件名称加载方向刚度k0/kN·mm-1Δy/mm屈服点Py/kNθ/mradΔm/mm极限点Pm/kNθ/mradΔu/mm破坏点Pu/kNθ/mrad延性μYL1推89.927.56395.554.2070681.2738.4670579.0838.469.26拉-90.29-7.52-390.40-4.18-60-682.16-33.33-70-579.84-38.469.31YL2推69.109.97408.195.5250677.5527.7870575.9238.467.02拉-69.54-9.66-406.79-5.37-50-678.79-27.78-70576.97-38.467.25YL3推45.3514.79440.498.1960659.1730.3370560.2938.464.73拉-45.71-14.25-435.81-7.93-60-651.97-30.33-70-554.17-38.464.91

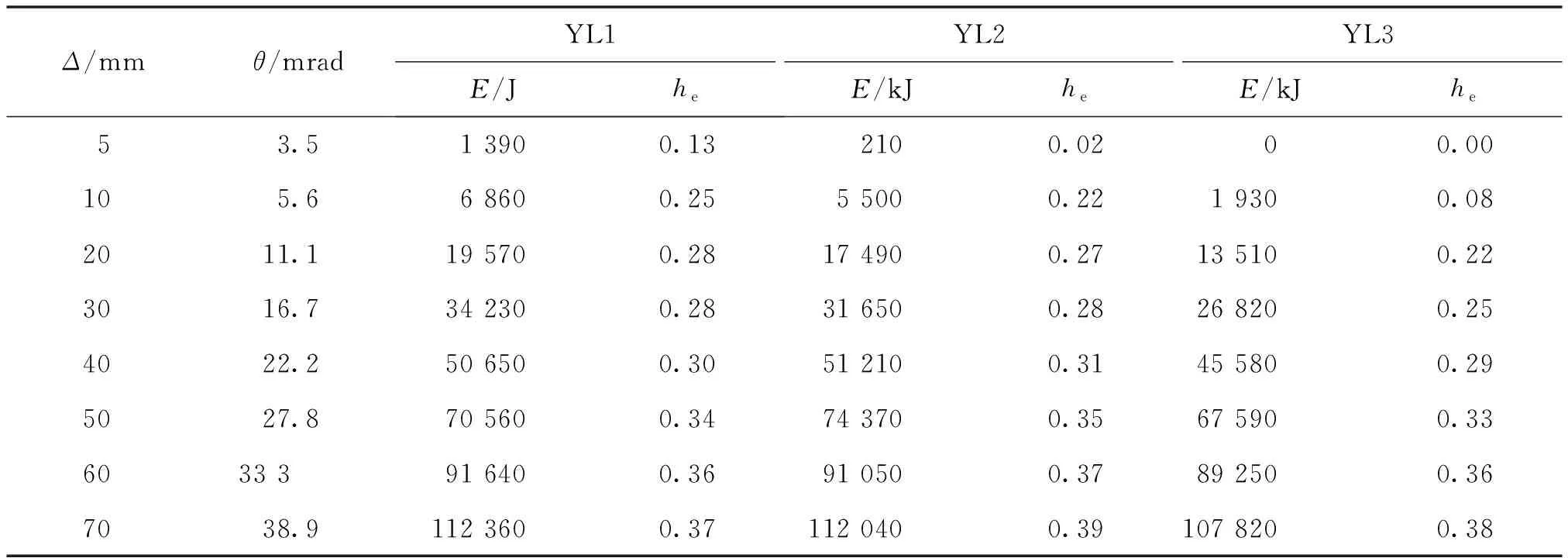
表5 耗能能力对比

3 震后可修复分析

3.1 构件应力分析

钢框架柱底部和耗能梁段上端截面的应力分析见图9，由图可知，YL1、YL2耗能梁段腹板的Mises应力较大，前者在第6级循环(40 mm位移)时屈曲，后者在第8级循环时屈曲；YL3腹板和翼缘的应力都比较大，在第8级循环时腹板屈曲，翼缘变形明显.

YL1、YL2、YL3三者框架柱底部截面应力分布相似，第4级循环之前，三者均处于弹性状态，之后翼缘逐渐屈服，第8级循环后，由于耗能梁段屈曲，框架承担的内力迅速增大，约2/3截面达到屈服应力.

3.2 耗能梁段转角与层间位移角

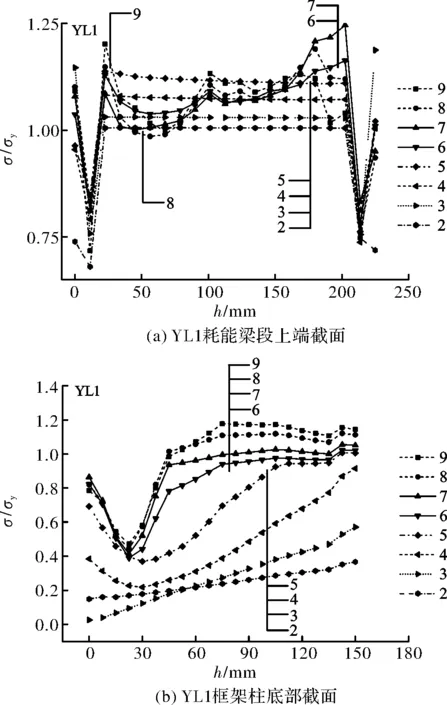
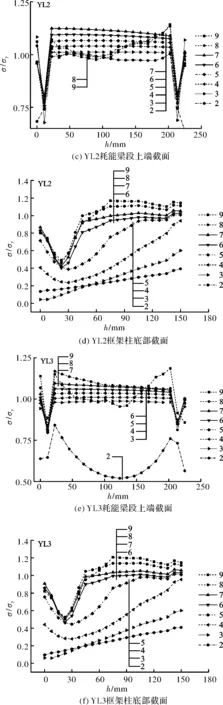
图9 构件截面Mises应力分布Fig.9 Section Mises stress distribution of structural members

HEY试件塑性铰力学模型见图10，γp为耗能梁段塑性转角，θp为框架层间位移角.耗能梁段的弹塑性变形能力可以用塑性转角γp=Δp/e衡量，美国AISC规范[18]规定剪切屈服型耗能梁段的塑性转角为0.08 rad；文献[19]的研究表明低屈服点耗能梁段的塑性转角可达0.20 rad，但未考虑框架的作用；文献[1]中剪切屈服型耗能梁段的塑性转角达到0.12rad.

耗能梁段塑性转角与框架层间位移角之间的关系见表6，由表可知，文献[20]规定的弹塑性层间位移角为0.02，相同塑性转角条件下，耗能梁段越长，所需要的层间位移越大，引起的框架梁的弯矩越大，塑性铰出现在框架梁的端部，甚至断裂[1].

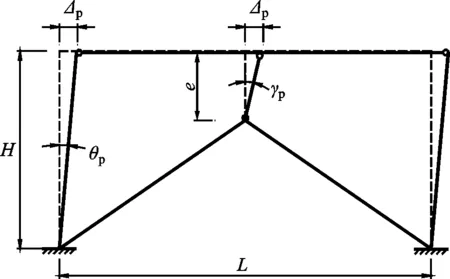
图10 HEY试件塑性铰力学模型Fig.10 Plastic hinges model of specimens HEY

θp/adγp/radθp/γp(e/H)e/mm0.02[19]0.08[17]0.254500.02[19]0.12[1]0.152700.02[19]0.20[18]0.10180

在耗能梁段长度选取的时候应考虑梁段塑性转动能力与框架层间位移角的变形协调关系，防止耗能梁段的弹塑性变形尚未充分发挥而框架已变形严重，造成震后修复困难.综上，Y形偏心支撑钢框架耗能梁段长度e不宜超过0.25H.

4 结论

(1)耗能梁段长度Y形偏心支撑钢框架初始刚度和刚度退化影响较大，对极限承载力影响较小.

(2)在0.02层间位移角之前，耗能梁段越短，耗散能量越多；0.02之后，三者相差很小.

(3)为保证耗能梁段工作性能和震后可修复性，Y形偏心支撑钢框架耗能梁段长度不宜超过0.25H.