一种基于Mark点的点胶机器人视觉目标定位方法

彭刚，熊超，夏成林，林斌

在3C行业的印刷电路板(PCB)制造过程中，为了实现点胶机器人对目标的定位，常采用Mark点辅助的方式。首先，机器人系统对PCB上的Mark点进行视觉定位，然后根据Mark点与目标的相对位置关系，可计算出目标位置。其中，Mark点定位精度直接影响点胶精度。通过优化Mark点识别与定位算法，可以提高操作的定位精度和可靠性，从而有效地提高产品质量。当前常用的Mark点定位方式有霍夫曼圆变换[1-3]、Surf、Sift特征匹配[4-6]等算法，其中霍夫曼圆变换可以适应更多类型的Mark点，但该算法的准确度易受到圆的图像规则度影响，一般还需结合其他复杂方法[7]才可保证准确度。而Surf和Sift方法准确率虽高，但实时性不佳。本文则从工程应用角度对Mark点定位算法的旋转不变性、缩放不变性、实时性、可靠性等方面综合考虑，对常用Mark点定位算法的实验结果进行分析比较，提出了一种基于Mark点几何特征的改进模板匹配算法。

1 简单模板匹配的Mark点识别算法

1.1 简单模板匹配原理

模板匹配[8-10]的原理相对简单，如图1所示，(a)是待检测图S，(b)是模板图T。使用模板图T依次从左至右，从上至下移动扫描图S的每1个像素。每移动1个像素匹配1次结果，扫描完毕就可找出最佳匹配结果。

1.2 常用的几种简单模板匹配算法的比较

模板匹配类型包括相关匹配、标准相关匹配、平方差匹配、标准平方差匹配、相关系数匹配和标准相关系数匹配[11]。这里使用相关匹配、平方差匹配、相关系数匹配分别进行实验并对比，匹配效果如图2所示。

图2 3种匹配方法结果Fig. 2 Results of three template matching methods

从匹配的结果来看，平方差的效果最好。平方差模板匹配公式如式(1)，结果为0时匹配效果最好，值越大匹配效果越差。

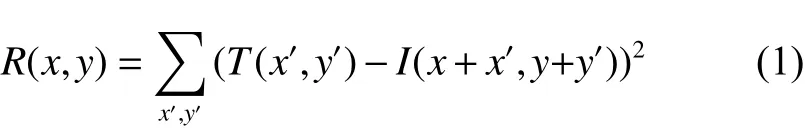
2 Mark点几何特征的改进型模板匹配算法

2.1 Mark点图像的特征分析

PCB板上的Mark点一般都是在印刷时通过敷铜制成，常由圆形和其他常见几何图像组合而成，本文所使用的Mark点的灰度图像如图3所示。从Mark点的灰度图可知其显著特征：正中心白实心圆，八边形轮廓，最外围大圆轮廓，其余都近似是黑色。

图3 Mark点图像Fig. 3 Mark point

除此之外，大圆轮廓外部的图像是冗余信息且具有不确定性，Mark点信息只包括大圆轮廓内部图像。

2.2 Mark点图像预处理

相机拍摄的图像一般为彩色图像，为了利于后续操作需将其转换成灰度图并进行二值化。为了使边界更加清晰，还可对图像进行锐化处理，锐化方法主要分为梯度锐化和拉普拉斯锐化法。本文采用后者，假设是拉普拉斯算子，分别对图像函数计算垂直和水平方向的二阶偏导，两者之和就是拉普拉斯算子[12-14]，如式(2)～(4)所示：

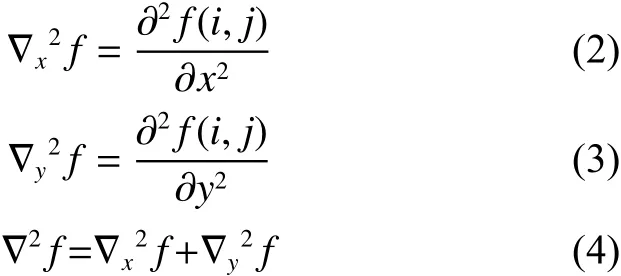
对于扩散现象引起的图像模糊，可用式(5)作锐化处理[15-16]。

锐化操作会放大图像的部分孤立噪声，所以在锐化前需滤除这些噪声。本文的孤立噪声滤波方式是判断白色像素的邻域是否全为黑色像素，若是则将当前像素置为黑色。图4(a)是二值化图，图4(b)是单点滤波图，图4(c)是锐化图，从这几幅图可以看出它们的对比效果。

图4 Mark点对比Fig. 4 Comparison of mark point images

2.3 改进型模板匹配算法对Mark点的识别与定位

2.3.1 根据几何特征提取Mark点结果集

根据本文2.1节的Mark点几何特征分析，可知Mark点几何特征主要包括3部分：小实心圆、八边形轮廓、外围大圆轮廓，具体如图5所示。

图5 Mark点特征Fig. 5 Features of mark point

为了让轮廓更加清晰，根据上述2.2节对待检测图进行二值化、滤波和锐化等预处理。图像预处理完成后，就可以根据几何特征提取疑似目标集[19-20]。

本实验中，已知标准Mark点图片最小尺寸为80×80。在此基础上，对待检测图从左至右、从上至下逐像素地按步骤进行搜索：

1)以待检测图的左上角首个像素点为起始中心点，判断该像素是否为白色，若否，则返回，若是则如图6所示继续从中心点沿上下左右搜索各方向第一个黑点，并记录黑点位置。因为小圆半径不超过80像素，故可限定搜索半径为80像素。4个方向都搜索到黑点后就比较中心点与各黑点的距离是否基本相等，是则继续，否则返回。

图6 小圆搜索路径图Fig. 6 Search path of small circle

2)如图7所示，由于正八边形旋转周期是45°，所以从中心点起始并以45°为周期，到8个边的距离都相等。故以45°为周期，从当前中心点开始向8个方向搜索第一个八边形轮廓并记录位置。最后判断中心点到八边形各边的距离是否基本相等，是则继续，否则返回。第二个八边形搜索规则一样，从上一个八边形轮廓继续向前搜索即可。

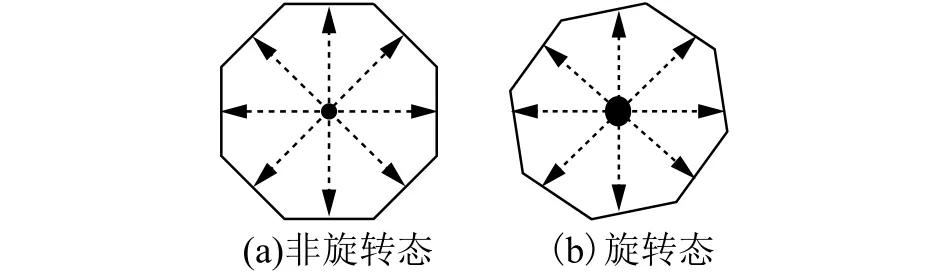
图7 正八边形搜索路径图Fig. 7 Search path of regular octagon

3)大圆的识别可以从步骤2)中搜索得到的外八边形轮廓开始，沿上下左右4个方向搜索并记录大圆轮廓的首个白像素点。最后判断中心点沿各方向到大圆轮廓的距离是否基本相等，是则计算出大圆半径，否则返回。因为在待检测图中几乎没有与大圆相近的目标，故可根据霍夫圆变换和大圆半径参数进一步确认所得大圆轮廓是否正确。

若上述3个条件都满足要求，就可以将搜索得到的疑似Mark点目标保存到结果集中。具体的搜索决策流程如图8所示。

图8 决策流程图Fig. 8 Decision-making flowchart

在实现时，为防止漏识别，搜索条件一般较宽松，最后得到的可能是一个结果集，所以还需要继续对结果集进行筛选。

2.3.2 根据改进型模板匹配算法对Mark点结果集进行筛选

本文采用改进型模板匹配法进行结果集筛选，为了准确地匹配有旋转和缩放的目标，需要计算缩放比例和旋转角度。假定结果集中的任一Mark点元素外围大圆半径值为r，且标准Mark点对应的该参数为R。同时，设内八边形轮廓与圆心在水平方向上的距离为L，且标准Mark点对应的参数为M；则缩放比例T和旋转角度的计算如式(7)、(8)所示。因为旋转包括两种相反方向的旋转状态，所以对应的旋转角也有两个值。

根据得到的缩放比例与旋转角，对标准Mark点进行相应的缩放和旋转变换校正，从而得到与结果集中Mark点有着相同缩放和旋转状态的Mark点模板图。由于标准Mark点大圆以外的冗余图像部分具有不确定性，故只截取并保留校正变换后Mark点的大圆内接正方形部分，并将该部分作为Mark点的新匹配模板，如图9所示。

图9 新匹配模板Fig. 9 New matching template

依次将结果集中的疑似Mark点元素与新的Mark匹配模板进行传统模板匹配操作，疑似Mark点元素的匹配区域是Mark点的大圆内接正方形部分。不断重复Mark点模板校正、截取及模板匹配步骤，计算并保存各个结果集元素的匹配值。最后对匹配结果进行比较，选取最佳匹配结果，具体的Mark点搜索流程如图10所示。

图10 Mark点搜索流程图Fig. 10 Mark point search flowchart

3 实验结果对比

3.1 实验条件

图11为本文实验使用的样本，(a)是待检测图，大小为522×391；(b)是Mark点模板图，大小为 160×160。

图11 待检测图和模板图Fig. 11 Test image and template image

在主频2.53 GHz的CPU，4 GB内存，Windows7系统的电脑上，使用基于MFC和OpenCV2.4.9开发的图像识别软件，进行以下实验测试。

3.2 Sift和Surf算法对Mark点的识别效果

根据前面引言部分所述，Sift和Surf算子都可用于Mark点识别，本文为了清晰地展现各种算法的优劣，特别对Mark点特征图像在缩放和旋转变换条件下使用Sift和Surf两种算法进行识别实验，实验数据如表1和表2所示。

表1 缩放对比实验结果Table 1 Comparsion of image scaling experiment

表2 旋转对比实验结果Table 2 Comparsion of image rotation experiment

从表中数据可以分析出：Sift算法匹配用时是Surf的2～3倍，Sift在图像缩小变换后的匹配效果也不如Surf；但是Sift算法的有效匹配点对数一般都比Surf多，尤其是在旋转状态下。由此可见，两种算法在Mark点匹配中各有一定优缺点。

3.3 传统平方差模板匹配算法对Mark点识别效果

根据OpenCV库中的平方差模板匹配算法，对经过不同比例缩放(无旋转)后的待检测图进行测试，测试结果如表3所示。其中待检测图像指标类型为1.0倍，表示未经缩放的待检测图。

表3 平方差在模板缩放时的匹配结果Table 3 Matching results of square difference in different template scaling

从缩放后的匹配结果可以得出：匹配效果随着待检测图的缩放程度增大而变差。显然，该算法不太适合。

3.4 改进型模板匹配算法对Mark点的识别效果

为了清晰地比较改进型模板匹配算法与Sift、Surf、平方差模板匹配算法之间的优劣，在相同实验条件下进行实验。

1)测试经过缩放的PCB板图像。分别对缩放倍数为0.6、0.9、1.5和2.0倍的待检测样图进行测试，测试耗时分别为125、194、363和513 ms，匹配效果如图12所示。

2)测试经过旋转的PCB板图像。分别对旋转度数为45°、60°和120°的待检测样图进行测试，测试耗时分别为484、455和442 ms，匹配效果如图13所示。

图13 旋转后的匹配结果Fig. 13 Matching results after images rotation

根据上述测试结果可得出：提出的基于Mark点几何特征的改进型模板匹配算法识别效果良好。从算法的时间复杂度上看，改进模板匹配算法的平均速度是Surf的2～3倍，满足实时性要求。从缩放旋转上看，改进的模板匹配算法同时具有旋转和缩放不变性，且误差在5个像素以内，满足实际应用中的可靠性与准确性要求。

4 结束语

Mark点作为常用的视觉辅助定位对象，使用Sift、Surf和简单模板等传统匹配算法对其进行识别时，不能很好地同时满足缩放旋转及实时性等要求。本文提出了一种基于Mark点几何特征的改进模板匹配算法，针对待检测图像的缩放旋转状态，对匹配模板进行相应的缩放旋转变换，不仅实现了对缩放变换的良好适应性，还保证了良好的实时性。应用该算法的视觉系统可以准确可靠地识别出Mark点并定位，从而可以根据相对位置关系实现对PCB目标点的准确定位。相比当前常用的Mark点定位算法，该算法保证了较高准确率，同时提高了实时性，可以适应当前不断提高的视觉定位实时性要求，具有较好的工程应用价值。