求解离散优化问题的元胞量子狼群演化算法

2018-09-18马龙卢才武顾清华

智能系统学报 2018年5期

马龙，卢才武，顾清华

（西安建筑科技大学管理学院，陕西西安 710055）

在人工智能计算和系统工程等领域中，许多离散空间优化问题常具有解的多样性、动态性以及目标函数收敛速度慢等特点。为了在有限的空间环境下快速搜寻到优化问题的最优解，学者们已对多种智能算法进行融合并展开了广泛的研究和应用。

狼群演化算法(wolf pack evolutionary algorithm，WPEA)作为模拟自然界群狼分工协作捕猎的启发式智能优化算法，1970年美国著名专家Mech[1]在其著作中对狼群的行为特征进行了详细的描述；2014年Mirjalili等[2]将该算法与金字塔模型进行结合，提出了一种具有等级森严的狼群捕猎层次模型，该算法在解决实数空间问题的应用效果明显。此后针对离散空间优化问题，文献[3]针对分类特征子集的优化问题，提出了二进制狼群演化算法；文献[4-5]提出了一种改进的二进制狼群演化算法，扩展了狼群演化算法的应用范围；Srikanth等[6]在深入分析狼群演化算法的基础上，针对组合调度优化问题，提出了二进制量子狼群演化算法(quantum wolf pack evolutionary algorithm，QWPEA)。QWPEA算法相对于WPEA算法具有原理简单、参数设置少、收敛速度快、较强的全局搜索能力等特点，在测试函数和实际工程应用中取得了突出的效果[7-8]。但这些应用都是以固定的搜索空间和种群个体位置的静态更新为基础进行优化求解，对于离散空间中局部和全局的并行演化以及狼群中的个体狼的量子位置旋转角的动态选取和调整问题，QWPEA算法并没有一个有效的解决方法。

元胞自动机(cellar automation，CA)最早由冯诺伊曼在1966年提出[9]，CA是一种根据简单的并行演化规则和协同更新方法，采用元胞来模拟复杂的离散系统动力学方法[10]，CA具有时空动态性、状态离散性和同步性等基本特征。

为了解决有限的离散空间内狼群演化算法的收敛速度慢、搜索能力弱以及易于陷入局部最优等问题，提出了一种求解离散优化问题的元胞量子狼群演化算法(cellar quantum-behaved wolf pack evolutionary algorithm，CQWPEA)，该算法主要采用二进制编码方式和元胞自动机中的演化规则，分别实现量子狼群中的个体狼位置与猎物之间的距离以及量子旋转角的选取和调整，并给出了头狼与猎物资源位置的编码方式，同时给出了探狼和猛狼局部搜索算子的编码方式，分析了编码规则。另外，采用泛函分析方法对该算法的收敛性进行了证明，最后通过6个测试函数验证了CQWPEA算法的有效性和合理性。

1 量子狼群演化算法

为了使量子狼群算法适应离散搜索空间寻优问题，受二进制编码量子粒子群演化算法[11]的启示，在量子狼群演化算法中引入二进制编码，融合元胞自动机演化规则，提出了求解离散优化问题的元胞量子行为狼群演化算法。为分析方便，首先对元胞自动机原理、二进制量子狼群演化算法中的狼群行为规则、头狼产生规则、狼群更新和变异等演化方程进行描述。

1.1 元胞自动机原理

元胞自动机通过利用大量元胞的并行演化规则来模拟复杂结构和过程，成为探索复杂系统的有效工具[12]。CA协同更新元胞空间中的所有元胞，协同更新的规则：下一个时刻元胞i的状态是由自身和邻居在前一时刻的状态来决定的。元胞状态集、邻居、元胞空间以及局部演化规则作为CA的基本组成要素，其邻接类型主要有两种，即Von.Neumann 型和 Moore 型，如图 1 所示。

元胞自动机的动态演化规则以元胞的动态时间状态变化集合为基础，其可表示为

CA由一个标准的四元组构成，其形式为

1.2 量子狼群算法

1.2.1 量子狼群编码

在量子狼群演化算法中，人工狼编码是以一组量子位和二进制表示，每个量子位的状态可用式表（6）示：

人工狼当前位置的编码可通过量子位的概率幅表示，考虑到狼群初始化时编码的随机性，假设采用量子方式编码的个体为，则编码方式为

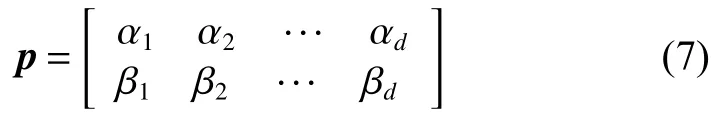
式中： | α|2表示量子态被观测为 |0 〉态概率， |β |2为量子态被观测为 |1 〉态概率，满足 |αi|2+|βi|2=1；i =1,2,d;d为编码位数。

由此可知，量子狼群可表示为Q (q)=(qg1,qg2,···,qgn),其中， g 表示进化代数，n表示个体狼数量；(i=1,2,···,n)表示第 g 代狼群中第 i只狼，即

1.2.2 双策略的初始量子位生成过程

在初始化狼群演化过程中，狼群中每匹狼位置的所有量子位对应态的概率幅可采用Logistic混沌映射产生，其产生的基本过程为：

1) 设狼群规模为 n，个体狼位置编码的长度为 d；

式中：μ为混沌因子， 0 ≤µ≤4；k为迭代次数。当µ=4， 0 ≤xkj≤1时，Logistic完全处于混沌状态。

5) 计算全部 2n个个体的适应度值并进行排序，选取个适应度值高的个体狼构成初始狼群。

1.2.3 头狼产生规则

在初始解空间中，将最接近猎物资源(或最优目标函数)的个体狼视为头狼，头狼直接进入迭代过程。算法运行中，通过比较每匹人工狼的量子位状态，获得当前狼群迭代过程中的最优个体狼作为头狼，最终求解得到头狼的位置和最佳适应度。第 j个位上的量子位状态可表示为

式中： ( s1,s2,···,sj)表示量子状态位对应于人工狼的二进制表示形式； r andom[0,1]表示在 [0 ,1]之间的随机数， j =1,2,···,d。

在传统的进化算法中，与狼群算法的“优胜劣汰生存”规则和遗传算法的“轮盘赌”规则不同的是，本文设计了一种基于滑模原理的交叉量子位遗传演化方法，用于将选择之后产生的候选头狼集合中的个体头狼按优秀程度降序排序，然后从染色体右端低量子位开始与头狼染色体按照滑模方式交叉，式(11)和式(12)表示交叉参数呈高斯分布，随着候选个体头狼逐渐陷入局部解，如图2所示，交叉点滑模按照式(13)向左移动，用于分别与新一代头狼迭代，产生更优秀后代头狼。

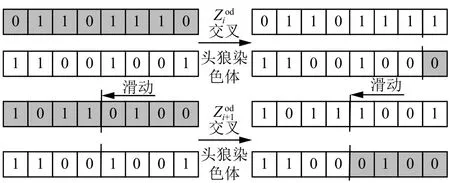
图2 候选头狼染色体量子位滑模交叉方法Fig. 2 The sliding mode crossover of quantum bits of candidate lead wolf

交叉权值分布函数为

式中： Ziod=(Zio,1d,Zio,2d,···,Zio,dj),j∈ L 表示第i匹候选头狼染色体量子位 j 从最优至次优串排列；i=1,2,···,N;j=1,2,···,d。

交叉权值为

式中I表示当前候选头狼数量。

滑模位置为

1.2.4 狼群位置更新

在QWPEA中，当滑模交叉结束后，采用上次迭代过程中的最优解对狼群中的每一个量子位进行量子旋转门更新，更新过程如式(14)。

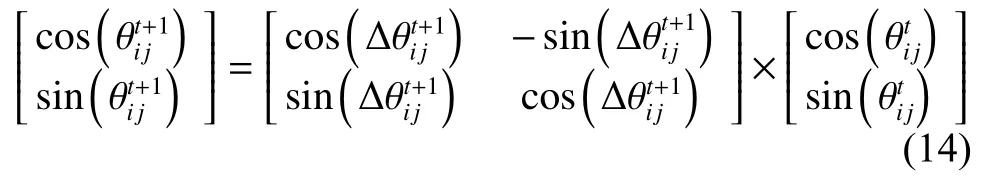
由此可知，量子旋转门是通过改变描述量子人工狼位置的相位角来实现人工狼在搜索空间位置的同步移动。

1.2.5 量子狼群变异

为了避免算法陷入局部最优解状态，维持狼群的多样性，以平衡维猎场空间内随机分布的人工狼和决策变量可行域为基础，实施智能猎杀行为后，基于优胜劣汰的生存法则，会有匹人工狼被淘汰，并会有新的R匹人工狼存活下来，但存活与淘汰的人工狼数量要相等，这样既可维持狼群规模数量，也可避免算法的过早收敛和全局搜索能力差的问题。因此，狼群中个体狼的变异过程采用量子非门实现，其表达形式为

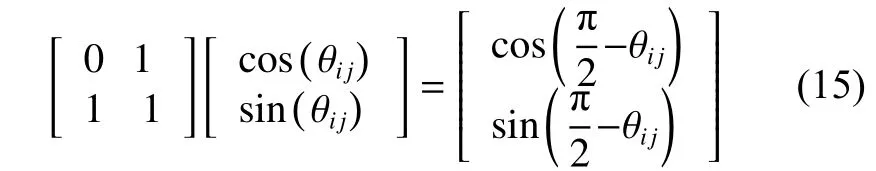
式中： θij表示量子旋转角； i =1,2,···,N； j =1,2,···,d。

假设变异概率为 pm，每个人工狼在 (0 ,1)之间给定一个随机数random，如果 ra ndom＜pm，则随机选择若干个量子比特，用量子非门交换两个概率幅，而其旋转角度向量保持不变。

1.2.6 量子人工狼群行为描述

1) 四处游走行为

假设量子人工探狼的当前状态为pi，在其感知的目标猎物资源信息为 fi ti=f(xi)的范围内随机选择一个位置状态 pj，如果 fi ti＜fitj，这时探狼i代替头狼发起召唤行为；如果 fi ti＞fitj，则探狼i向P个方向按照游走步长前进一步继续侦察；如果此时探狼i 感知的猎物气味浓度为，则自主决策后沿着猎物留下的气味最浓且大于当前位置 pi的方向 p∗前移一步，同时对探狼i的位置pi进行更新。反复执行上述行为，直到 fi ti＞fitj，或者游走次数 T 达到最大游走的次数 Tmax。其中选择的方向 p∗应满足式（16）：

在人工狼群中存在的个体探狼有着不同差异，嗅探猎物资源的方式也不同，因此可取不同的 h 值，h 可取 [hmin,hmax]之间的随机整数。而在 d维空间中，探狼 i 沿着 p (p=1,2,···,h)个游走方向前移一步后所处的空间位置为

式中：p 表示判断游走的方向数；γ表示在 [− 1,1]间均匀分布的随机数； s tepds为第 d维的游走步长；表示探狼的位置。

2) 嚎叫召唤行为

假设量子人工头狼的当前状态为 pi，头狼采用嚎叫召唤行为召集周围的 Mnum匹猛狼向其位置集合，其中 Mnum=N−Snum−1；接到头狼召唤的猛狼都以较大的奔袭步长 st epdb快速逼近头狼所在的位置 pd，即在第 d 维空间，猛狼 j 经历第 k +1次迭代的位置为

猛狼在向头狼聚拢的过程中，如果猛狼 j 感知的猎物气味浓度 fi ti＞fitj，则令 fi ti=fitj，此时猛狼 j转换为头狼并发起召唤行为；如果 fi ti＜fitj，则猛狼 j继续快速奔袭，且与头狼 fi tj间的距离dis＜dnear时，即转入围攻。则判定距离 dnear可表示为

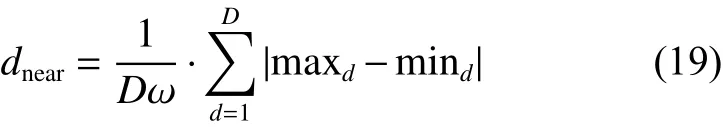
式中：ω为距离判定因子； D 为空间维数；maxd、mind分别为待寻优的第 d维空间变量的最大值和最小值。

3) 智能猎杀行为

假设量子人工头狼的当前状态为 pi，将距离猎物资源最近的头狼所在位置 pd看作猎物的位置。 fi tkid可视为在第 k 代狼群中在第 d维空间中猎物的位置信息，狼群的智能猎杀行为表达为

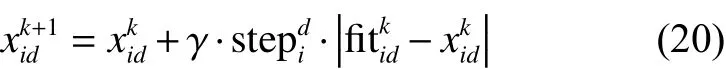
式中： γ ∈ [−1,1]为均匀分布的随机数； s tepdi表示人工狼i (猛狼和探狼)在维空间中智能步长数。

式中：S 表示步长因子，S值越小人工探狼搜索越精细。

2 元胞量子狼群演化算法

在CQWPEA算法中，人工狼(头狼、探狼和猛狼)的位置表示为一组0、1构成的二进制编码向量，首先通过使用概率统计方法对个体狼与猎物之间的最优平均位置值进行编码，并记录编码位中出现的0、1次数，实现局部搜索算子编码位的计算；然后，采用元胞自动机选取和调整人工狼群位置的量子位旋转角，增强元胞量子狼群演化算法的搜索空间，加快算法的收敛速度。

CQWPEA的设计思路是，将散布在猎场空间中的量子狼群中的探狼朝着猎物遗留的气味浓度强和环境信息方向进行嗅探，一旦发现猎物，探狼需要判断自身与头狼距离猎物资源的位置，如果探狼与猎物的量子位置旋转角比头狼与猎物的量子位置旋转角大，则探狼代替头狼发起嚎叫召唤行为，否则向头狼报告猎物的位置信息；猛狼收到嚎叫召唤信号后，猛狼迅速向头狼所在位置或猎物所在位置靠拢，同时对猎场的周围环境进行探测，量子狼群进化算法中的人工狼之间以嚎叫信息实现相互通信，并通过元胞机中的局部演化规则不断调整人工狼的位置旋转角度，更好地调节人工狼群的搜索范围和定位猎物的位置，随着局部搜索过程的不断推进，人工狼群向着全局最优解逼近，最终通过计算头狼与猎物的平均最优位置来实现目标函数的优化求解。

2.1 个体狼位置的二进制编码

在二进制编码的元胞量子狼群演化算法中，为了精确描述狼群中头狼与猎物资源之间的距离关系，将元胞空间作为量子狼群演化算法的搜索空间，将距离猎物资源最近的头狼所在位置看作猎物资源(目标函数)的位置，使用量子狼群进化算法中的探狼、猛狼搜索到的局部最优解和猎杀攻击后的全局最优解分别作为元胞空间内一个元胞，并采用扩展Moore邻居类型，采用数学语言对元胞量子狼群演化算法进行形式化描述。

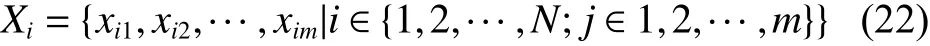
式中： N 表示人工狼总数，m表示编码长度； xij表示人工狼的第 Xi个位置的第 j个编码位置，通过反置赋值操作且只能取0、1；头狼 p 和猎物资源 q之间的曼哈顿距离可表示为

定义2 移动算子[5]，设人工狼i 的位置为Xi={xi1,xi2,···,xij,···,xim}； M 表示非空的反置编码位，即表达了人工狼的位置；r是非空的反置编码位数，即游走步长；运动算子 θ (Xi,M,r)表示在人工狼i 的位置 Xi中，从 M 个编码位中随机选择 r个编码位并对其进行反置操作。

定义3 设集合C =(c1,c2,···,ci,···,cn),ci∈ {0,1}，ci的排列组合构成元胞空间，其具体形式为

式中CellX表示由 ci所组合的元胞。

定义4[7]扩展Moore邻居类型

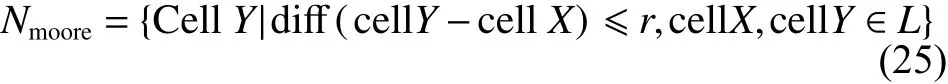
式中：任意两个 ci、ci+1的排序组合的差异度为diあ(cellY−cellX)≤r ，r 为差异度，本文取 r = 2。

在二进制编码的元胞量子狼群演化算法中，为了精确表达头狼和猎物资源之间的距离，根据定义1，假设头狼和猎物的位置为 (X1,X2)，它们分别有两个决策变量 (X11,X12)、 ( X21,X22)，采用6位二进制编码对每个决策变量进行表示，如图3所示。

图3 头狼与猎物位置的二进制编码Fig. 3 Location of the lead wolf and prey with binary encoding

在CQWPEA算法中，定义头狼与猎物(目标函数)含有决策变量的个数即为元胞空间的维数；例如， Xid表示狼群中第i 匹头狼的 d个决策变量， Xi、Xid的二进制编码长度分别用l 和 ld表示，则

根据量子狼群演化算法，通过修改算法中的头狼和猎物之间的平均最优位置的值，生成CQWPEA中的，并用二进制位串表示种群中全部最优个体狼位置，通过概率统计方法[6]，记录二进制编码位中0、1出现的概率次数，如果0出现的次数多，则对应的值为0，否则为1，如图4所示。

图4 人工狼与猎物之间的平均最优位置值Fig. 4 The optimal average position between the artificial wolf and prey

从图4中可知，狼群中有5个最优位置值，每个个体狼当前的最优个体信息分别为、、、、，其第1列对应的二进制位值为1、 0、1、 0、 1，依据概率统计方法，则对应的第1列二进制值为1，以此类推。由此获得的的值为1000011110001。特别地，如果对应的每一列中的二进制位数中出现相同的0或1，则随机选择0或1。由此可构造出CQWPEA算法中的函数值。

在QWPEA算法中，式(17)、(18)是探狼和猛狼在整个搜索空间的局部位置信息，其值表示了局部搜索算子 pid， pid∈(pbesti,gbestd)，pid={pi1,pi2,···,piD}位于 ( pbesti、gbest)之间的对角线两端的超矩形中，pid到 pbesti,gbest的距离需小于对角线的长度，即

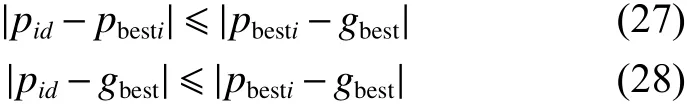
通过对 pid值的计算，可使种群产生多样性，并可使算法跳出局部搜索空间。在QWPEA算法中，局部搜索算子 pid的产生主要取决于上一代种群的 pbesti和 gbest中的每一个量子位的随机交叉，形成下一代的搜索算子 pid，显然满足定义1的曼哈顿距离，如图5所示。

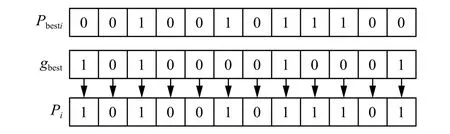
图5 人工狼的多点交叉算子Fig. 5 Multi-point crossover operator of wolf

探狼和猛狼的局部搜索算子， pdi、pdj的每一位编码可由式(29)与(30)计算获得：

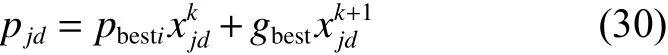
式中 γ ∈ [−1,1]内的随机数。由此可构造出直接计算 pid与 pjd值的函数[6]。

2.2 基于CA的量子旋转角选取策略

在QWPEA算法中，新一代个体狼的概率幅是由上一代个体的概率幅与量子旋转门更新计算获得，更新过程如式(31)：

设每匹狼i的 n −1个邻居构成的集合为Si(t)={x1(t),x2(t),···,xn(t)}。在解算个体狼的邻居集合最优解时引入以下演化规则[13]：

式中： St与 St+1分别表示t 与 t+ 1时刻元胞状态；s表示元胞邻居集合中状态为1的元胞个数。设第g代狼群当前解集第 i匹狼的局部最优解为1,2,···,n)，狼群的全局最优解为则量子门旋转角的更新策略如式(34)所示：

式中 T 与 Tmax分别表示当前迭代次数和最大进化迭代次数。

为了增强量子狼群演化算法搜索范围，将量子旋转角进一步扩展到，使狼群遍历范围呈现双向性。另外，由于量子态经测量后获得二进制编码，因此按式(36)进行取值：

由式(36)可知，本文算法中的量子旋转角扩大了3倍，呈现双向性，避免了混沌序列的迭代计算和多次比较的查表操作，节省了运算时间。

2.3 CQWPEA算法的步骤

1) 初始化参数，根据1.2.2节的双策略对量子狼群的初始量子位进行初始化，并采用二进制序串的形式初始化狼群中的个体狼位置，使，计算初始狼群个体的适应度值，同时对算法的基本参数进行初始化操作。

4) 根据初始狼群的适应度函数值计算种群中每个个体狼位置值，并与上一次迭代的局部最优值进行比较，如果适应度值，则用更新局部最优位置；反之，则不更新；转入步骤5) 。

5) 量子人工狼按照式(31)～(36)进行元胞邻域搜索，并计算狼群体中新的适应度值。将狼群的全局最优位置值与上一次的全局最优位置值进行比较，如果，则替换原最优位置值，反之，不更新。另外在量子旋转角中，如果，对狼群的量子编码位进行交叉，交换量子位概率幅与。

6) 按头狼产生规则和猎物气息元胞邻居空间的演化规则对头狼位置进行更新，邻域搜索同4)。

9) 输出目前的最优解集和最优值。

3 CQWPEA算法的收敛性分析

本节将用泛函分析方法[13-14]对CQWPEA算法的收敛性进行分析证明。令二进制编码字符集，采用长度为的二进制位串表示头狼位置编码，编码空间。假设狼群规模为，狼群单钱位置集合为，头狼最佳位置集合为，则狼群的当前位置空间可表示为

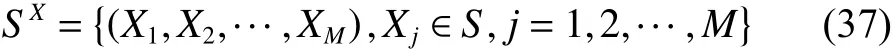
狼群中人工狼的最佳位置空间为

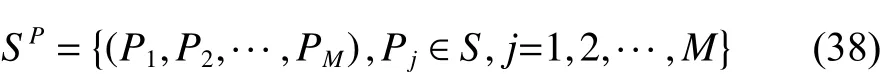
全局最优解的位置空间为

根据QWPEA算法的流程图[6]可知，QWPEA算法的解算过程遵循着反复迭代，逐渐求精的过程，该过程中包括目标函数适应度值的评价、位置和位置的选择，以及人工狼的位置更新，从而使狼群达到更优状态。因此，可用随机映射运算过程来抽象表示QWPEA算法的流程。

定义5 CQWPEA算法的搜索算子T是通过逐步迭代方式对个体狼的当前位置进行迭代搜索，以获得个体狼的最好位置的过程，该过程是从人工狼当前位置的元胞状态空间以及全局位置的元胞状态空间随机映射到个体狼最好位置状态空间，其映射形式为

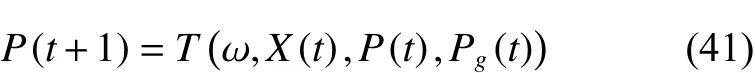
实验表明，CQWPEA算法中每一代全局最好解位置的适应度值序列是一个递增序列，即

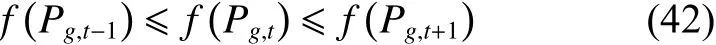
在CQWPEA算法中，解算优化问题时，通常只需关注搜索过程中狼群攻击获得的最好解，不妨将迭代狼群体用全局最好位置来代替。由此对CQWPEA算法的映射过程进行重新定义，其形式为

在CQWPEA算法中，解算优化问题的过程可视为元胞演化空间之间的映射。以下采用随机映射的方法证明和分析CQWPEA算法的收敛性。

证明首先证明 (S ,d)是度量空间。设 S ≠Ø，d∈S×S的实值函数。对于 Pg,i、Pg,j、Pg,k∈ S，对应一个实数 d Pg,i,Pg,j∈S满足：

其次证明 (S ,d)为完备度量空间。设 S是有限的二进制编码位串{数，对当}前狼群中最好个体狼位置的柯西序列( Pg,i,Pg,i∈S，以及 ∀ ε＞0， ∃ N，当自然数 n ＞N 时， d Pg,n,Pg,m＜ε，当 n → ∞时， Pg,n→Pg。因此 (S ,d)是完备的度量空间。

最后证明 (S ,d)是可分的。设 G ⊆S ，因 S为有限元集合，所以 G 为可数子集。又因为 G 闭包于 S，所以 G 在 S 中稠密，由此得到 (S ,d)是可分的论证。故 (S ,d)是完备可分的度量空间，证毕。

定义7 随机搜索算子 T :Ω×S→S称为随机压缩算子，如果 ∃ K(ω)＜ 1的非负实值随机变量，则

证明依据CQWPEA原理，每迭代一次均可产生比上一次更优的个体狼和目标猎物资源，所以存在一个非负实值随机变量 K (ω)∈ [0,1)，使得

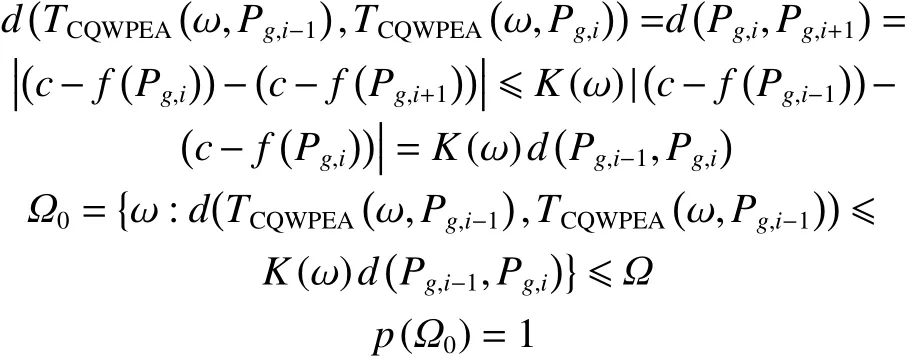
定理2 (随机压缩映射定理)设随机搜索算子 T :Ω×S→S 满足所有的 ω ∈S ， T (ω)均为压缩算子，即 ∃ Ω0∈ Ω,p(Ω0)=1，对 ∀ ω ∈ Ω0，则d Tω,Pg,i,则Pg,i,Pg,i−1,Pg,i+1∈ S,0≤ K(ω)＜1，则 T (ω)有唯一随机不动点 r (ω)，即T(ω,r(ω))=r(ω)。

然后证明r ( ω)的可测性。对 ∀ Pg,0∈S，令Pg,1(ω)=TCQWPEAω,Pg,0，Pg,i+1(ω)=TCQWPEAω,Pg,i,i=1,2,···,因为 Pg,1(ω)→Pg,0，TCQWPEAω,Pg,i(ω)→TCQWPEA(ω,Pg,0,Pg,i∈S，即 TCQWPEA(ω)连续。依据符合定理，Pg,i为一个随机变量序列，再根据巴拿赫压不动点定理可知， Pg,i(ω)→ r(ω)，根据极限随机变量定理的定义，r (ω)作为一个随机变量，因此 r (ω)作为TCQWPEA(ω)的随机不动点，证毕。

4 实验仿真与结果分析

4.1 测试函数

为了检验CQWPEA算法的寻优性能，选取6个标准的测试函数进行仿真实验，6个测试函数的表达式如下：

1) Sphere函数

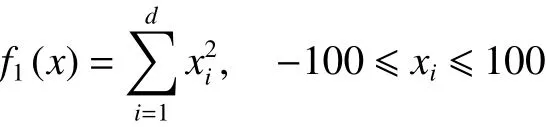
2) Schwefel函数

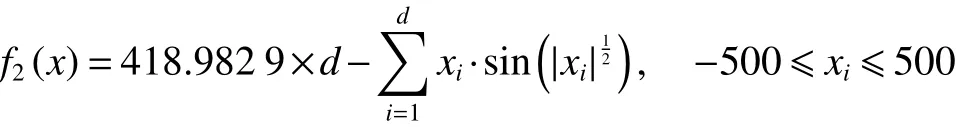
3) Rosenbrock函数

4) Rastrigrin函数

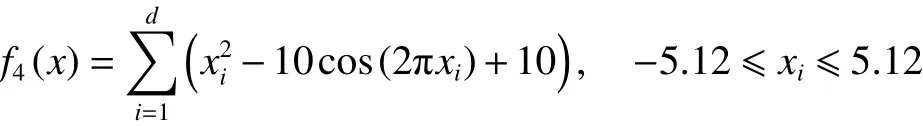
5) Ackley函数

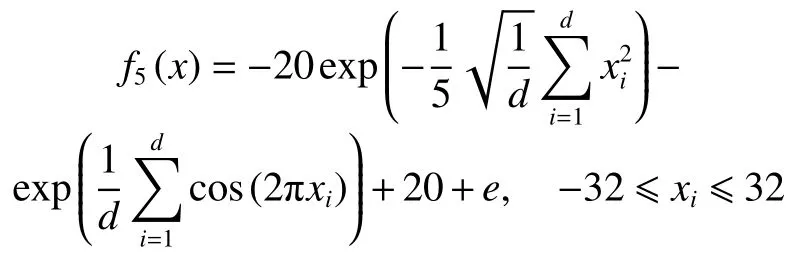
6)Griewangk函数

在上述6个标准测试函数中， f1(x)、 f2(x)和f3(x)为单峰函数， f4(x)、 f5(x)和 f6(x)为多峰函数，函数的维数均设置为30，6个标准测试函数的全局最优解均为0。

4.2 仿真结果分析

采用CQWPEA算法对6个标准测试函数进行解算，并将其结果与WPEA、QWPEA算法的结果进行比较。其中相同的参数设置为：狼群规模均为500，最大迭代次数为500次，收敛精度设置为0.000 01。具体到每个不同算法的参数，在WPEA算法和QWPEA算法中，判定因子，步长因子，更新因子，最大游走次数，探狼比例因子，滑模交叉，，,。在CQWPEA算法的控制参数，量子旋转角，实验仿真环境：Windows7系统，3 GB内存，4 GHz CPU，算法基于MATLAB2015a。每种算法的终止条件均为满足算法的寻优目标或达到最大迭代次数，计算结果见表1所示。各取每个算例20次的实验数据，记录其最优值、平均值、最差值；并将CQWPEA算法的结果与WPEA和QWPEA算法进行比较，分别记录其平均迭代次数、最大迭代次数、收敛率以及20次独立运行消耗的总时间。为了增加算法的可信度，WPEA和QWPEA算法的参数直接来源于参考文献，优化比较结果如表2所示。表2中的“—”表示对应的寻优成功次数指标无法获得统计结果。

表1 6个测试函数的结果比较Table 1 Experimental results of six test functions

从表1的结果可知，在满足固定收敛精度下，本文提出的CQWPEA算法分别在维度为10、20和30的基础上进行测试，发现除了Schwefel函数、Rosenbrock函数和Ackley函数外，其他3种函数经过20次实验均能一致性收敛到问题的全局最优解0。针对函数，CQWPEA算法和QWPEA算法均可获得最优解，而WPEA算法的寻优能力较差；针对函数，3种算法均无法获得最优解，但几乎可达到近似最优解；针对函数，3种算法虽然无法获得最优解，但CQWPEA算法要比其他2种算法获得的近似最优解更为接近最优解值0；针对函数，CQWPEA算法的寻优能力最强，WPEA算法的寻优能力要比QWPEA算法强，这主要是因为设置算法参数的不同而造成的；针对函数，虽然3种算法均没有获得最优解值，但从总体上来看，CQWPEA算法获得的最优解几乎接近全局最优解，其寻优能力较强，而QWPEA算法和WPEA算法获得的最优解距离全局最优解相差甚远；针对函数，CQWPEA算法可获得全局最优解，WPEA算法的寻优能力要比QWPEA算法强。

由上述分析结果可以得出，从总体上来看，本文提出的求解离散优化问题的元胞量子狼群演化算法在寻优能力均要优于其他狼群演化算法和量子狼群演化算法，但从部分函数测试的结果可知，本文算法对于部分函数也会存在无法获得全局最优解问题，这主要是因为算法的初始参数设置的随机性、局部寻优结果差、元胞演化规则对量子旋转角的调整速度慢、量子相位角的选择不精确等原因造成的。

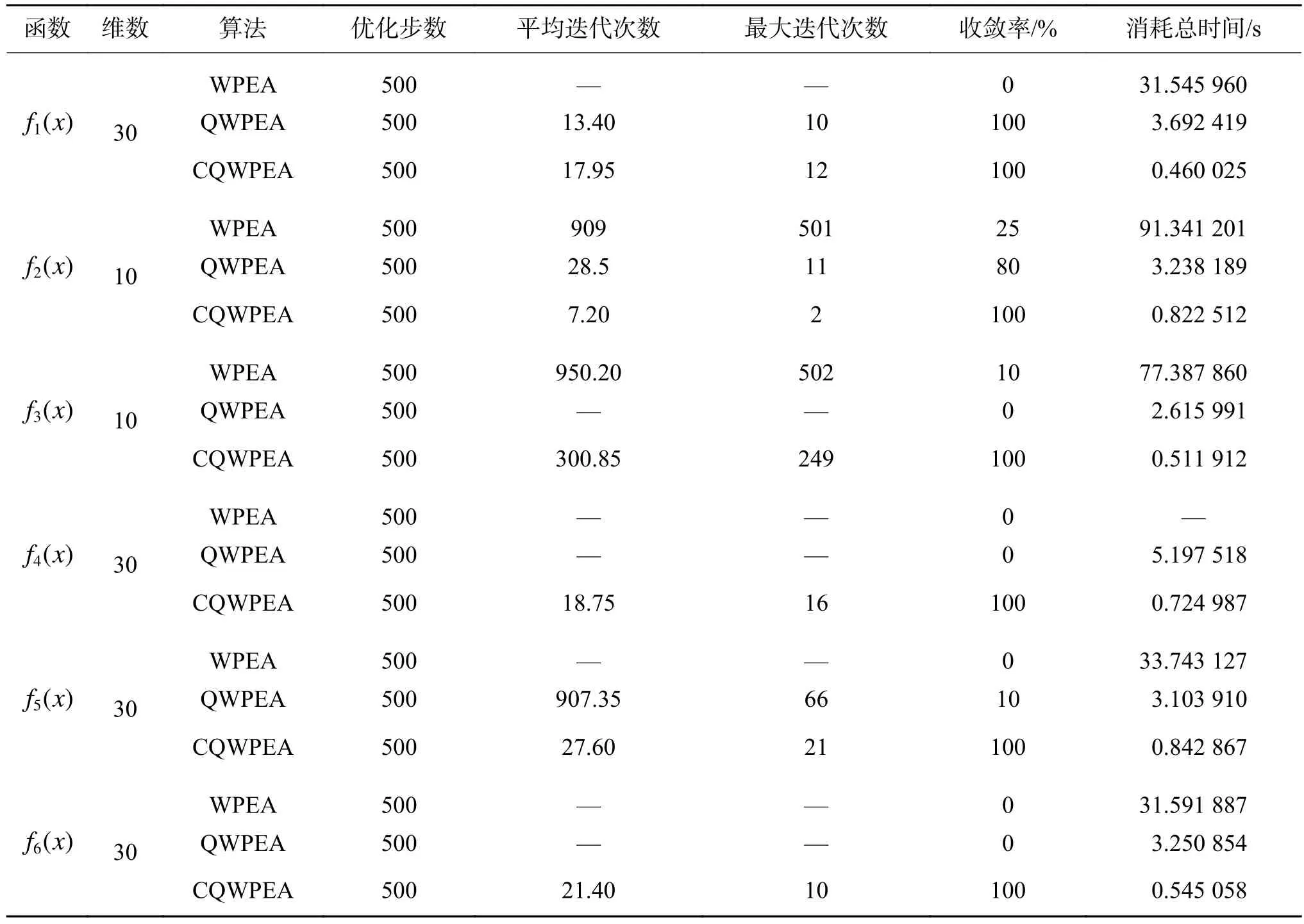
表2 迭代次数比较Table 2 Comparison of iterations

由表2的结果可知，在不同的维数和相同的优化步数下，从收敛率和消耗时间上来看，对于6种不同的标准测试函数，CQWPEA算法收敛率均可到达100%，且消耗时间明显比WPEA算法和QWPEA算法少；但对于不同的函数，3个算法的性能还存在一定的差异。对于f1(x)函数、f4(x)函数、f5(x)函数和f6(x)函数，WPEA算法的寻优结果不理想，主要是因为当维数大于3时，这4个典型的凹函数呈现多峰特征，具有大量的局部极值点，因此找到全局最优解较为困难。对于f3(x)函数、f4(x)函数和f6(x)函数，QWPEA算法的寻优结果的收敛率为0，其搜索到的最优解与目标函数的最优解的偏差较大，这是因为这3个函数是复杂的非线性多峰函数，寻优过程中会使算法陷入局部收敛；对于f2(x)函数和f3(x)函数，QWPEA算法的收敛率也几乎为0，其搜索到的最优解偏差也较大。

由上述的比较结果知，与WPEA算法和QWPEA算法相比，无论从收敛精度还是收敛稳定性方面，CQWPEA算法的寻优性能明显优于其他2种算法。

另外，从算法收敛(达到收敛精度)时间方面，WPEA算法对6个标准测试函数20次实验的收敛消耗总时间分别为31.55、91.34、77.39、33.74和31.59 s，而QWPEA算法对6个标准测试函数20次实验的收敛消耗总时间分别为3.69、3.24、2.62、3.20、3.10和3.25 s，CQWPEA算法对 6个标准测试函数20次实验的收敛消耗总时间分别为0.46、0.82、0.52、0.72、0.84和 0.55 s。从收敛消耗总时间来看，与WPEA算法和QWPEA算法相比，CQWPEA算法的收敛速度明显加快。从图6中可清晰地看出，CQWPEA算法要比WPEA算法和QWPEA算法具有较快的收敛速度。