基于瑞利波法对混凝土表面裂缝检测的数值研究
2018-09-18杜文卫江刚朱彬占周小平原志杰李金鑫
杜文卫,江刚,朱彬占,周小平,原志杰,李金鑫
(1. 贵州省铜仁公路管理局,贵州 铜仁 554300;2.贵州大学 土木工程学院,贵阳 550003;3.重庆大学 土木工程学院;山地城镇建设与新技术教育部重点实验室,重庆 400045;4.国家山区公路工程技术研究中心,重庆 400060)
瑞利波是一种沿半无限弹性介质自由表面传播的偏振波,具有波长长、振幅大等特征,被广泛应用于地质工程勘探、材料无损检测等领域[1-4]。瑞利波在层状介质中的应用,已经有比较成熟的理论和算法[5-8]。而在非层状介质中,瑞利波正演分析解析法只能针对个别特殊情况,对于更复杂的一般情况(比如混凝土结构中的裂缝、空洞等缺陷),瑞利波频散方程无法建立和求解,因此,只能选取数值模拟分析方法。最常用的数值模拟方法为有限单元法及有限差分法。郭君[9]、李春花[10]和叶唐进[11]等在二维平面内对瞬态瑞利波法探测介质内部空洞的相关参数进行了详细的分析。欧阳凯[12]基于幅值衰减、传播时间延时和频率阻隔规律,运用ANSYS有限元软件对表面垂直缺陷进行了分析,提出了利用瑞利波检测材料表面缺陷深度的方法。
本文基于上述研究,结合瑞利波的勘探原理[13-16],提出了材料表面裂缝长度和角度的计算公式,并应用有限元软件ABAQUS进行模拟分析,将模拟结果与公式计算结果对比,验证了公式的准确性。
1 计算方法理论(传播时间差法)
如图1所示,在裂缝左侧边缘处施加一个激励源,要求激励源的中心频率对应的波长远小于裂缝的长度。因此,在实际应用中选用高频激励源,以确保瑞利波沿着裂缝的两个侧面进行传播,并到达裂缝右侧的上表面。如图1(a)所示,在激励源的作用下,混凝土介质中产生3种弹性波;纵波、横波以及瑞利波。纵波直达速度最快但能量较弱,在实际应用过程中很难测到,所以,在有限元模拟过程中不予考虑。横波和瑞利波传播速度相近,在较短传播距离之内很难将其分离出来。如图1(b)所示,当瑞利波传播到裂缝底端时,一部分瑞利波会在裂缝底端经过模式转换形成衍射纵波和衍射横波,并以裂缝底端为中心,在混凝土介质内部向四周呈球状式扩散传播。其中,衍射纵波最先传播到裂缝右侧上表面,之后衍射横波也传播到裂缝右侧上表面,而且这两部分衍射波能量都比较大。衍射纵波最早到达裂缝右侧上表面的特点,在波形图中可以很快地确定,便于用来对裂缝的角度进行判断。
此外,另一部分瑞利波到达裂缝底端后,在裂缝底端会出现绕射现象,沿着裂缝表面右侧继续向上传播,最后到达裂缝右侧混凝土介质上表面,根据瑞利波的传播时间与激励源滞后时间差可以计算裂缝长度。

图1 瑞利波的传播及衍射示意图Fig.1 The diagram of Rayleigh wave propagation and diffraction
2 混凝土表面裂缝数值模拟分析
2.1 模型建立及参数设置
如图2所示,材料采用混凝土,弹性模量E=30 GPa,泊松比μ=0.3,密度ρ=2 500 kg/m3。模型尺寸大小选为长L=300 mm,宽L/2=150 mm,裂缝宽度1 mm。裂缝与水平方向的夹角为θ,裂缝长度为d,接收点的位置位于裂缝右侧60 mm处,激励源作用在裂缝左侧边缘,且中心频率设置为f=200 kHz。由式(2)、式(3)和式(4)可计算出瑞利波波长λR=10 mm。裂缝长度设置均远大于10 mm,满足利用传播时间差法计算的要求。
(1)
(2)
(3)
(4)
式中:λR为瑞利波波长;λ为拉梅系数;μ为泊松比;G为剪切模量;E弹性模量;ρ为密度;VP为纵波波速;Vs为横波波速;VR为瑞利波波速。

图2 有限元模型示意图Fig. 2 The schematic diagram of finite element model
如图3所示,激励源选用雷克子波,其表达式为
F(t)=A[1-2π2f2(t-t0)2]e-π2f2(t-t0)2
(5)
式中:t0为激励源滞后时间;A为幅值。

图3 激励源波形(中心频率为200 kHz的雷克子波)Fig. 3 The excitation source(the center frequency of Ricker wave is 200 kHz)
取t0为5×10-6s,幅值A=1×10-12m,具体波形如图3所示。采样时间间隔为
(6)
式中:Δt为采样时间间隔;f为中心频率。
根据式(6)可得,选用采样时间间隔2×10-7s,总共采样时间为2×10-4s。模型网格采用三角形网格,其尺寸选择中心频率(f=200 kHz)对应的瑞利波波长的1/10,即1 mm,共计45 000个单元。计算边界采用粘弹性人工边界[17]。
2.2 表面裂缝长度的计算
2.2.1 垂直裂缝长度的确定(即θ=90°) 选取激励源频率为200 kHz作用下的混凝土(裂缝长度为60 mm)波场快照,分析弹性波在含有表面裂缝的混凝土介质中的传播规律,并进行表面裂缝计算。
如图4(a)所示,当t=2×10-5s时,在激励源作用下,混凝土介质中产生弹性波,纵波和横波呈圆弧式向混凝土内部扩散,瑞利波在混凝土介质表面呈地滚式传播。纵波传播速度最快,而横波和瑞利波传播速度相近。如图4(b)所示,当t=4×10-5s时,沿裂缝表面传播的瑞利波已经到达裂缝底端,瑞利波一部分在裂缝底端发生模式转换,转换成衍射体波,其能量比较强。因为此刻瑞利波刚传播到裂缝底端,产生衍射体波的时间较短,所以,很难将衍射纵波和衍射横波分离出来;另一部分绕过裂缝底端继续沿裂缝右侧表面向上传播,形成很明显的绕射现象。如图4(c)所示,当t=5×10-5s时,瑞利波已传过裂缝底部,此时,一部分瑞利波沿裂缝右侧向上传播;另一部分则通过模式转换成衍射纵波和衍射横波,两者可以清楚地分辨出来。衍射纵波的传波速度(在同一种介质中,纵波的传播速度均相等)较快,衍射横波的传播速度相对衍射纵波较慢。但衍射横波的能量比衍射纵波大得多。另外,从图4(c)可以看出,纵波已经传递到模型底端,其能量被粘弹性人工边界吸收。如图4(d)所示,当t=6×10-5s时,由于衍射纵波传播速度快,首先到达混凝土表面,且首先被接收到,而衍射横波依旧在混凝土介质内部呈圆弧式扩散传播。同时,衍射纵波和衍射横波的能量出现了不同程度的衰减,其中,衍射纵波的能量衰减最大。如图4(e)所示,当t=8×10-5s时,衍射横波也传播到混凝土介质表面,能够接收到衍射横波,衍射纵波已经全部被粘弹性边界所吸收。经过裂缝后的瑞利波也到达混凝土介质表面,也可以在混凝土介质表面设置接收点接收该部分瑞利波的波形。如图4(f)所示,当t=1×10-4s时,裂缝右侧的瑞利波沿着混凝土介质表面继续呈圆弧式向右传播,衍射横波已经传播到模型底部边界,被粘弹性边界吸收。另一方面,在裂缝左侧传播的瑞利波已经完全被模型左侧粘弹性边界所吸收,并且横波也同样被模型左侧以及模型底部的粘弹性边界完全吸收。
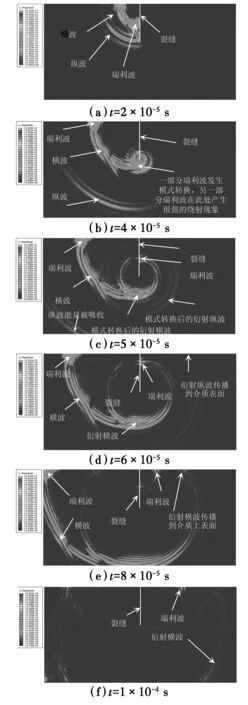
图4 各个时刻的弹性波场快照(裂缝长度为60 mm)Fig. 4 Snapshots of each time in the wave field(The length of crack is 60 mm)
如图5所示,根据接收到的计算波形,提取图形中峰值点A、B对应的时间,即为瑞利波和纵波到达接收点的时间。因为瑞利波经过裂缝两侧表面传播到混凝土介质表面,相对于衍射横波及衍射纵波,瑞利波传播时间最长,且自身的能量很强,因此,在计算的波形图中很容易找到瑞利波到达接收点处对应的特征点,即传播时间最长和幅值最大点,如图5中所标注的A点。另外,衍射纵波传播速度最快,因此,到达接收点的时间最快,且能量最小,其达到时间点为图5中标注的B点所对应的时间。
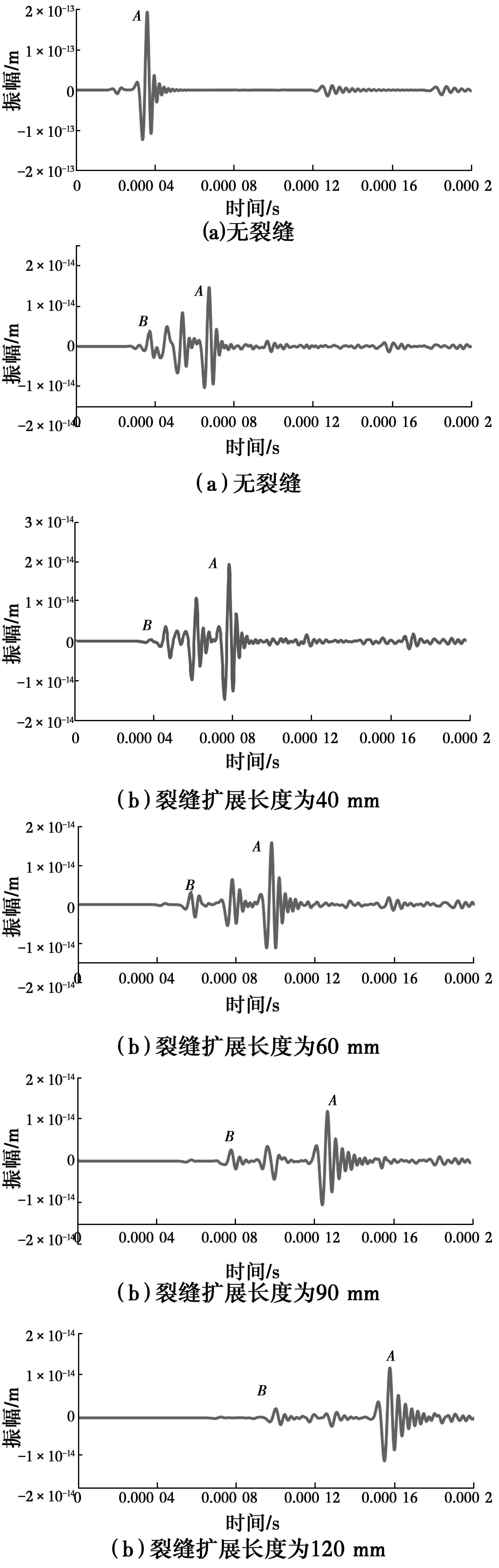
图5 计算波形图Fig. 5 Waveform diagram
根据图2的几何关系,以及接收到的计算波形图中的特征点A、B所对应的时间,即瑞利波、纵波的到达时间,可以得到裂缝长度的计算公式
(7)
式中:d为裂缝长度;a为偏移距;t0为激励源的滞后时间;VR为瑞利波波速,由式(3)可得VR=1 993 m/s;tR为瑞利波到达接收点的时间。
为了正确获得裂缝的长度,首先应在计算获得的波形图中确定波形峰值特征点(A)的位置,通过波形图可以读出其对应的时刻(tR),此时刻与激励源峰值对应时刻(t0)之差即为瑞利波从激励源处到达接收点处的时间差,这样,瑞利波的传播距离可以很容易地求出。通过弹性波的传播规律以及结合图4可知,瑞利波沿着裂缝左右两侧表面传播,之后沿着混凝土介质表面传播到接收点处。基于以上原理,利用瑞利波的传播时间差,结合式(7)可以对裂缝的长度做出精确的判断。
分别取无裂缝、裂缝长度为0.03、0.004、0.06、0.09、0.12 mm这6种工况进行数值模拟,得到瑞利波、衍射纵波到达接收点的时间。然后,根据式(7)计算裂缝长度,并与设置裂缝长度相比较,进行误差分析。结果如表1所示。
从表1的计算数据可知,通过ABAQUS模拟计算的结果,误差在7.86%以下,均达到了比较高的精确度,满足实际工程的要求。另外,在裂缝长度一定范围内,随着裂缝长度的不断增大,计算得到的裂缝长度越来越接近真实值,即相对误差越来越小,说明该方法是比较准确的,能够很好地应用于混凝土表面裂缝无损检测。
2.2.2 不同角度裂缝长度的计算 不同角度裂缝的长度计算,均采用式(7)计算,不同角度裂缝长度的计算结果,见表2。

表1 表面裂缝长度计算数据Table 1 The calculated data of crack length

表2 裂缝长度计算数据Table 2 The calculated data of crack length
从表2的计算结果可知,计算的相对误差均小于3.74%,达到比较高的精确度,满足工程要求。这说明,有限元软件ABAQUS能够模拟含表面斜裂缝的混凝土,且计算结果比较精确。
2.3 裂缝角度计算
2.3.1 裂缝角度计算公式 显然,竖向裂缝为θ=90°的特殊情况。根据表1可以求得裂缝的长度,结合弹性波场快照(图6)分析可得衍射纵波的传播时间为
(8)
式中:tP为衍射纵波幅值到达时刻。那么,衍射纵波传播到接收点时所经过的距离c(裂缝底端到接收点的直线距离,m)可以表示为
(9)
由式(1)可得VP=4 019 m/s,结合图2,可根据三角形余弦定理得出裂缝角度的求解公式为
(10)

图6 t=5×10-5s时刻的弹性波场快照(裂缝长度为60 mm)Fig. 6 Snapshots of t=5×10-5s in the wave field(the length of crack is 60 mm)
同样,分别可以得出混凝土表面裂缝长度为3、5、30、60、90、120 mm时接收点的波形图,提取特征点A、B的时间,结合式(7)~式(10),可以求出裂缝与水平方向的夹角θ,具体计算数据如表3所示。

表3 裂缝角度θ(不同裂缝长度)计算数据Table 3 The calculated data of crack angleθ(different crack length)
结合式(7)~式(10),可以求出裂缝与水平方向的夹角θ。由表3中衍射纵波以及瑞利波到达接收点的时间,结合式(7)、式(9)可分别计算得到裂缝长度d、裂缝底端到接收点的直线距离c,m,进而可以得到夹角θ,具体计算数据如表3所示。由表3的计算结果可知,当裂缝长度为0.03~0.12 m时,利用该方法的计算结果比较精确(相对误差在6.33%内,最小误差仅为1.78%);当裂缝长度为3、5 mm时,虽然,裂缝角度相对误差为10.33%、7.78%,但计算角度值与实际角度值的误差也不大于10°。因此,式(7)~式(10)可以应用到表面裂缝角度的计算,同时,计算精度达到比较高的标准。
2.3.2 表面裂缝角度θ的计算 如图7所示,为了验证斜裂缝角度计算公式的准确性,对不同角度的裂缝进行有限元数值模拟。采用控制变量法,设置裂缝长度为90 mm,选取混凝土表面无裂缝以及裂缝角度θ=30°、45°、60°、75°、90°、105°、120°、135°和150°的10种情况进行分析,分别得到接收点的波形图,提取特征点A和B的时间,然后,根据式(10)计算裂缝角度,并与设置裂缝角度进行比较,作误差分析。结果如表4所示。
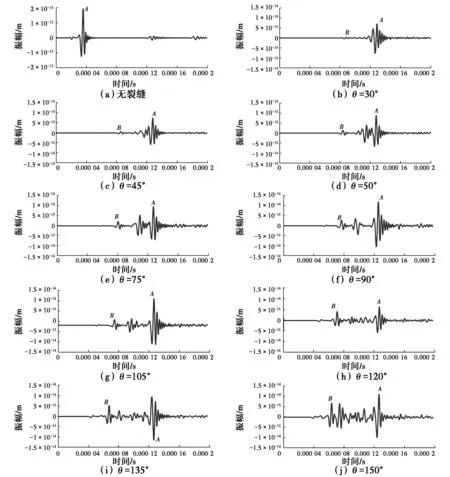
图7 计算波形图Fig. 7 Waveform diagram
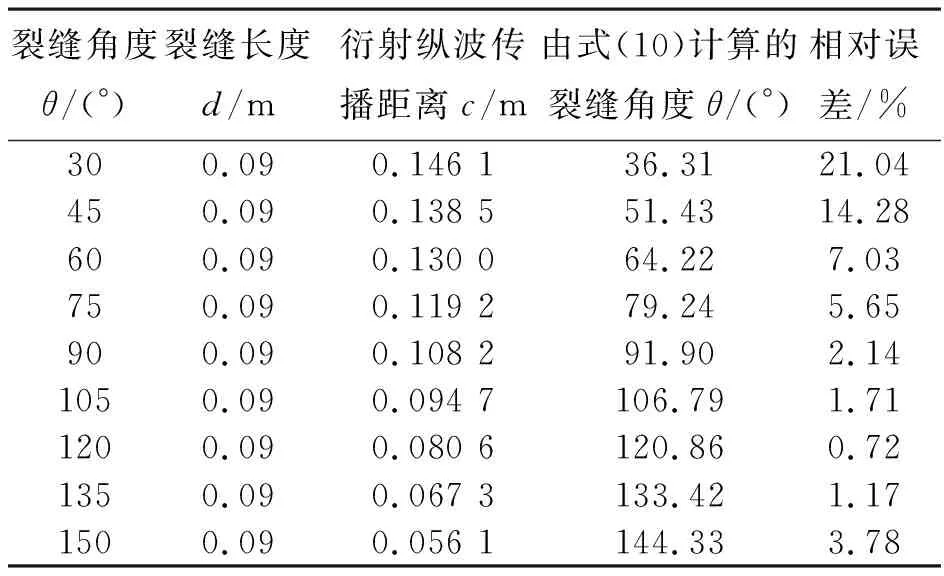
裂缝角度θ/(°)裂缝长度d/m衍射纵波传播距离c/m由式(10)计算的裂缝角度θ/(°)相对误差/%300.090.146 136.3121.04450.090.138 551.4314.28600.090.130 064.227.03750.090.119 279.245.65900.090.108 291.902.141050.090.094 7106.791.711200.090.080 6120.860.721350.090.067 3133.421.171500.090.056 1144.333.78
结果表明:当裂缝角度为75°~135°时,利用该方法的计算结果比较精确,计算角度值与实际角度值的差值不高于5°;当裂缝角度为30°~150°时,计算结果也较为准确;虽然,裂缝角度为30°和45°时,相对误差为21.04%及13.91%,但计算角度值与实际角度值的误差也不大于6.5°。
2.4 实验验证
为验证裂缝长度计算公式和裂缝角度计算公式的正确性,分别将得到的裂缝长度部分数值结果与曲华等[18]的实验结果进行对比,将得到的裂缝角度的部分数值结果与Matsuda等[19]的实验结果进行对比,对比结果分别见表5、表6。由表5可知,由数值模拟得到的裂缝长度与曲华等[18]实验的结果很吻合(相对误差在6.41%内);由表6可知,由数值模拟得到的裂缝角度与Matsuda等[19]的实验结果也很吻合(相对误差在12.11%内)。由此可见,提出的裂缝长度计算公式和裂缝角度计算公式是正确的。

表5 不同方法裂缝长度对比结果Table 5 Comparison of different methods of fracture length

表6 不同方法裂缝角度对比结果Table 6 Comparison of different methods of fractureangle
3 结论
1)应用有限元软件ABAQUS对含有表面裂缝的混凝土介质进行数值模拟,通过得到的弹性波波场快照,分析了弹性波的传播规律。在激励源作用下,产生横波、纵波和瑞利波,横波和纵波在介质中传播,最后被粘弹性人工边界吸收,而瑞利波在传播过程中,一部分瑞利波继续沿着裂缝表面传播;另一部分则在裂缝底端发生模式转换,形成衍射横波和衍射纵波。传播中,接收器能够接收到瑞利波和衍射横波、衍射纵波,得到计算波形图。最终,所有的弹性波被粘弹性人中边界吸收。
2)根据瑞利波在含有表面裂缝的混凝土中的传播规律,结合传播时间差法以及特征点法,提出了一种新的表面裂缝长度和裂缝角度的计算方法。对不同工况的裂缝进行计算分析,结果显示,其计算误差均在较低水平,满足实际工程要求,且在一定范围内,裂缝长度和角度随着其值的增大,得到的结果准确度越高。通过与实验结果相对比,验证了裂缝长度计算公式与角度计算公式的正确性。
参考文献:
[1] 崔建文, 乔森, 樊耀新. 瞬态面波勘探技术在工程地质中的应用[J]. 岩土工程学报, 1996, 18 (3):35-40.
CUI J W, QIAO S, FAN Y X. Application of transient rayleigh surface wave prospecting method to engineering geology [J]. Chinese Journal of Geotechnica1 Engineering, 1996, 18(3): 35-40. (in Chinese)
[2] 陈云敏, 吴世明, 夏唐代. 用表面波谱分析方法检测道路结构的质量[J]. 浙江大学学报, 1993, 27(3):309-314.
CHEN Y M, WU S M, XIA T D. Inspecting the quality of highway structures of spectral analysis of surface of waves method [J]. Journal of Zhejiang University, 1993, 27(3): 309-314. (in Chinese)
[3] ZHANG Y, XU Y X, XIA J H. Wave fields and spectra of Rayleigh waves in poroelastic media in the exploration seismic frequency band [J]. Advances in Water Resources, 2012, 49(8): 62-71.
[4] DARINSKII A N, WEIHNACHT M, SCHMIDT H. Finite element analysis of the Rayleigh wave scattering in isotropic bi-material wedge structures [J]. Ultrasonics, 2017, 73: 67-76.
[5] THOMSON W T. Transmission of elastic waves through a stratified solid medium [J]. Journal of Applied Physics, 1950, 21(2): 89-93.
[6] ROSEBAUM J H. A note on the computation of Rayleigh wave dispersion curves for layered elastic media [J]. Bulletion of the Seismological Society of America, 1964, 53(3): 1013-1019
[7] ZHANG S X, WANG Y, ZHOU H W, et al. Dispersion splitting of Rayleigh waves in layered azimuthally anisotropic media [J]. Journal of Applied Geophysics,2009, 67(2): 130-142.
[8] 柴华友, 张电击, 卢海林, 等. 层状饱和介质中瑞利波传播特性薄层分析方法[J]. 岩土工程学报, 2015, 37(6): 1132-1141.
CHAI H Y, ZHANG D J, LU H L,et al. Behavior of Rayleigh waves in layered saturated porous media using thin-layer method [J]. Chinese Journal of Geotechnica1 Engineering, 2015, 37(6): 1132-1141. (in Chinese)
[9] 郭君. 地下洞穴的瑞利面波波场特征有限元数值模拟研究[D]. 成都:西南交通大学, 2008.
GUO J. The underground cave’s Rayleigh wave field characteristic finite element numerical simulation study [D]. Chengdu: Southwest Jiaotong University, 2008. (in Chinese)
[10] 李春花.基于ANSYS的瞬态瑞雷面波法地下空洞勘测参数分析[D]. 成都:西南交通大学, 2011.
LI C H. Parameters analysis based on ANSYS in the underground caves survey by transient Rayleigh wave method [D]. Chengdu:Southwest Jiaotong University, 2011. (in Chinese)
[11] 叶唐进.瞬态瑞利面波法数值模拟中的参数硏究[D]. 成都:西南交通大学, 2012.
YE T J. Study of the parameters in ANSYS numerical simulation of transient Rayleigh wave method [D]. Chengdu:Southwest Jiaotong University, 2012. (in Chinese)
[12] 欧阳凯. 基于瑞利波的材料表面缺陷深度检测数值研究[D]. 哈尔滨:哈尔滨工业大学,2014.
OUYANG K . Numerical analysis of material surface defect depth detection using Rayleigh wave [D]. Harbin:Harbin Institute of Technology, 2014. (in Chinese)
[13] 杨成林. 瑞雷波勘探[M]. 北京:地质出版社, 2003.
YANG C L. Rayleigh wave exploration [M]. Beijing: Geological Publishing House, 2003. (in Chinese)
[14] 杨成林. 瑞雷波勘探原理及其应用[J]. 物探与化探, 1989, 13(6):465-468.
YANG C L. The principle and application of Rayleigh wave exploration method [J]. Geophysical & Geochemical Exploration, 1989, 13(6):465-468. (in Chinese)
[15] ZERWER A, POLAK M A, SANTAMARINA J C. Rayleigh wave propagation for the detection of near surface discontinuities: Finite element modeling [J]. Journal of Nondestructive Evaluation, 2003, 22(2):39-52.
[16] 练小聪.混凝土介质中瑞雷面波传播特性的研究[D]. 长沙:中南大学, 2014.
LIAN X C. The study of the Rayleigh wave propagation characteristics of the concrete medium [D]. Changsha:Central South University, 2014. (in Chinese)
[17] 刘晶波, 谷音, 杜义欣.一致粘弹性人工边界及粘弹性边界单元[J].岩土工程学报, 2006, 28(9):1070-1075.
LIU J B, GU Y, DU Y X. Consistent viscous-spring artificial boundaries and viscous-spring boundary elements [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9):1070-1075. (in Chinese)
[18] 曲华, 宁建国, 李学慧. 利用瑞利波频谱分析法无损检测混凝土结构[J]. 混凝土, 2006(2): 76-80.
QU H, NING J G, LI X H.Nondestructive testing of concrete structures using the spectral analysis of Rayleigh wave [J]. Concrete, 2006(2): 76-80. (in Chinese)
[19] MATSUDA Y, NAKANO H, NAGAI S, et al. Surface breaking crack evaluation with photorefractive quantum wells and laser-generated Rayleigh waves [J]. Applied Physics Letters, 2006, 89(17): 171902.
