双腹板工字形预应力钢箱混凝土盖梁抗弯性能分析

2018-09-14姚昌荣牟廷敏孙才志

四川建筑 2018年4期

陈功,姚昌荣,牟廷敏,孙才志

(1.西南交通大学土木工程学院，四川成都 610031；2.四川省交通运输厅公路规划勘察设计研究院，四川成都 610041)

[通信作者]姚昌荣(1974～),男，博士，副教授，研究方向为桥梁结构防灾减灾、结构损伤识别与健康监测。

预应力钢箱混凝土结构指在钢箱内灌注混凝土并张拉预应力而成的组合结构，能充分3发挥钢和混凝土材料各自的优点，与钢结构和混凝土结构相比，具有承载能力高，韧性和可塑性能好，施工便利和抗震性能优越等特点[1]；且能适应现代结构对于高荷载、大跨度和抵抗极端恶劣环境等方面的要求[2]。双腹板工字型预应力钢箱混凝土盖梁是由四川省交通运输厅公路规划勘察设计研究院自主研发的，具有更高的抗弯承载能力和抵抗变形的能力的新型结构。目前，国内外对于钢箱混凝土的研究多为不含预应力的普通钢箱混凝土，且以受压为主，受弯研究偏少[3]。国内外对于受弯性能的研究主要有：日本的Sakurai[4]，美国的Uy[5]，我国福州大学的韩林海[6]，西南交通大学的占玉林[7]，四川省公路院的牟廷敏[8]，等。但已有的研究，模型体量往往偏小，且截面以矩形为主，荷载水平较低[9]。为此，本文结合某工程利用有限元软件ANSYS进行双腹板工字型钢箱混凝土盖梁足尺模型的受弯行为模拟计算分析，通过采用双腹板工字型的截面构型、混凝土的灌注和预应力筋的张拉，达到延缓受拉区混凝土开裂，提高截面承载能力和延性，能应用于公路桥梁和铁路桥梁的目的，并为工程实践提供理论基础。

1 工程概况

某预应力钢箱混凝土盖梁采用双腹板工字型截面设计，在由Q345钢板焊接而成的钢箱内灌注C30混凝土，腹板内设置9根φ15.24预应力钢束，并张拉300 t预应力。盖梁结构见图1，截面如图2中的(B-4)所示。

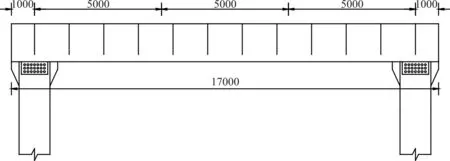
图1 双腹板工字形盖梁立面示意

2 非线性模型的建立

为了分析这种双腹板工字形预应力钢箱混凝土盖梁的受力特性，依照上述参数和图2所示截面，分别建立双腹板工字型钢箱梁(B-1)、双腹板工字型钢箱混凝土梁(B-2)、无翼缘预应力钢箱混凝土梁(B-3)和双腹板工字型预应力钢箱混凝土梁(B-4)的非线性有限元模型进行对比分析。

图2 盖梁截面示意

2.1 本构关系和破坏准则

核心混凝土受外包钢管约束，使其工作性能进一步提升,本构关系相比无约束混凝土发生了较大变化。本文采用基于文献[6]提出的约束本构模型，应力应变曲线如图3所示。

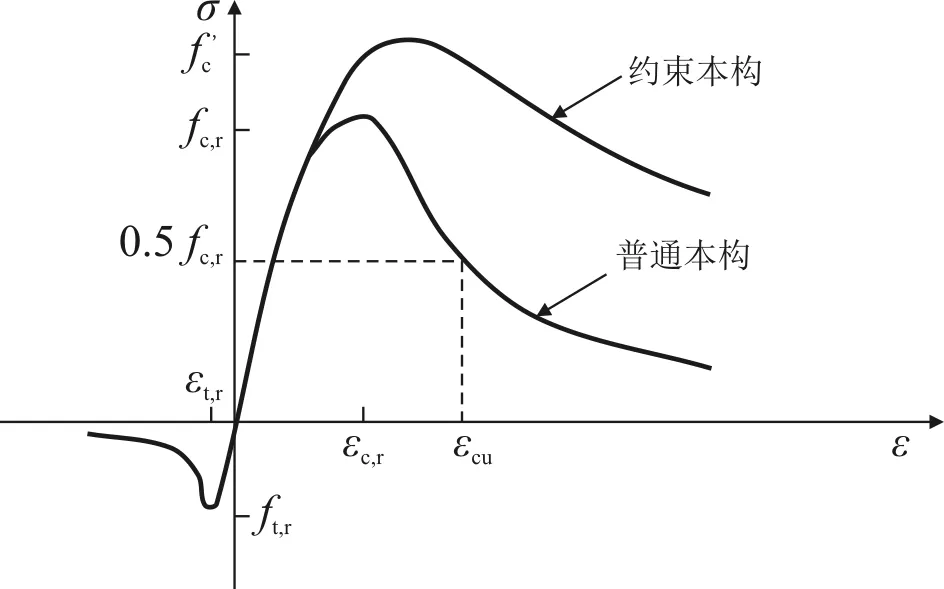
图3 混凝土应力-应变曲线

根据国内外试验及资料发现，在一定参数范围内，核心混凝土应力达到峰值之前，应力应变关系与素混凝土模型在形式上类似；而当应力水平达到峰值后，钢管混凝土核心混凝土约束本构关系主要和约束系数ξ有关。

(1)

式中：As为钢管横截面积；Ac为混凝土横截面积；fy为钢材屈服强度；fck为混凝土轴心抗压强度标准值；α为钢管混凝土截面含钢率。

由式(1)可知：ξ值越大，钢管对核心混凝土的约束作用越强，随着结构变形量的增加，本构关系曲线出现下降段越晚，甚至没有下降段；反之，ξ值越小，本构关系曲线越早出现下降段，且下降趋势随着ξ的增大而减小。

混凝土抗拉强度远小于抗压强度，且结构计算不考虑抗拉强度对承载能力的提升作用，因此通过破坏准则对混凝土的破坏进行考量。Willam-Warmker破坏准则是一种改进的五参数混凝土破坏准则，能够描述混凝土在静水压力作用下的单轴和双轴极限抗压强度。根据以往试验可知，W-W五参数准则对于约束本构混凝土模型具有良好的计算精度[6]。

顶部钢板受压时，可能发生局部屈曲，因此不考虑其进入强化阶段；底部钢板受拉时，其应力-应变关系采用二次塑流模型，并利用三段式弹塑性本构模型进行简化[10]；预应力筋弹性阶段采用直线段本构，当超过弹性极限后采用Ramberg-Osgood曲线近似模拟[11]。

2.2 单元的选择

混凝土模拟采用SOLID65单元，该单元是一种具有8节点的3D实体单元，每个节点具有3个自由度，同时具有开裂和压碎的性能，能用于模拟混凝土结构性能。该单元可模拟混凝土三个方向的开裂、压碎、塑性变形以及徐变，具有良好的非线性性能。

钢箱模拟采用SHELL181单元，该单元是一种4节点有限应变壳单元，每个节点具有6个自由度，可以模拟薄壳至中等厚度壳结构，同时能承受平面方向及法线方向的荷载。钢箱混凝土结构腹板位置钢板受到剪切作用明显，而SHELL181基于Mindlin-Reissner一阶剪切变形理论，可考虑到结构受剪切变形的影响。

预应力筋采用LINK8单元模拟，该单元是一种2节点3D杆单元，可模拟桁架、连杆和预应力钢索等。该单元每个节点具有三个自由度，可承受轴向拉压。单元初应变可通过Δ/L给定，Δ为单元长度L与零应变单元长度之差，可用于模拟预应力的施加。

2.3 荷载施加与收敛准则

在荷载施加的过程中，应避免应力集中导致局部屈曲或者混凝土过早地开裂以致分析过早的不收敛，因此本次模拟采用300 mm×200 mm面加载方式替代集中荷载加载。

模型采用位移控制法控制收敛，非线性计算的收敛受子步数与平衡迭代次数影响，为使结构容易收敛，采用5 %的位移收敛精度，且将平衡迭代次数提升至50次。

3 数值模拟

3.1 验证模型

为验证上述建模方法的可靠性，采用文献[1]中的矩形预应力钢箱混凝土梁S-2试验数据进行建模分析，并与试验值进行对比。模型参数见表1，得到荷载位移曲线见图4。由图中可看出：试验梁受钢板制造缺陷、混凝土裂缝等因素影响，在弹塑性阶段的非线性行为大于理论值，且有限元计算中采用的N-R迭代法无法越过极值点计算出下降段；而线性阶段和破坏阶段的计算结果与试验结果吻合良好。计算结果表明，该建模方式能够很好反应预应力钢箱混凝土结构的力学行为，因此按照这种方法来分析本文图2中的四种截面模型是可行的。

表1 验证模型参数表

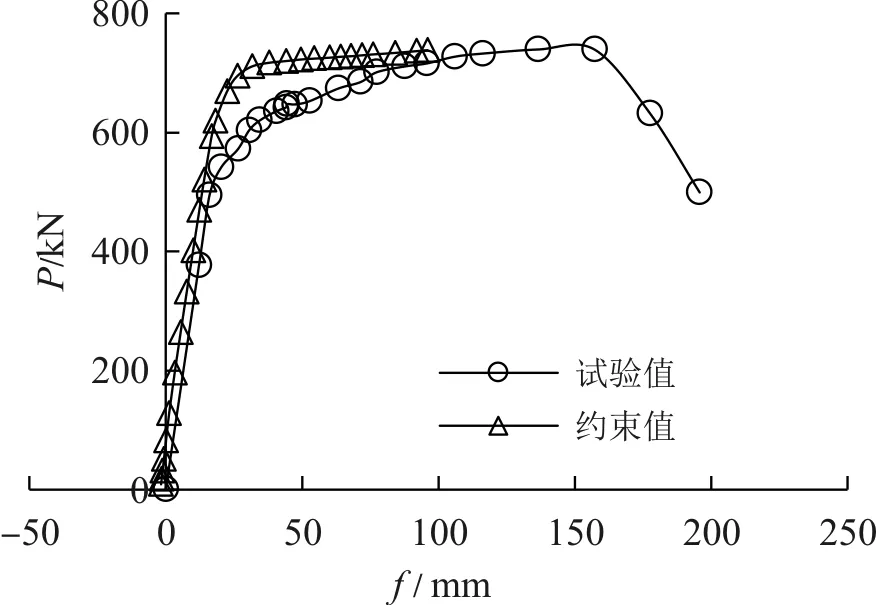
图4 混凝土荷载位移曲线

3.2 各截面形式计算分析结果

为了分析图2中不同截面形式梁的抗弯承载能力，按照上述方法，建立跨度为5.0m的简支梁有限元分析模型。以跨中底部位置的荷载挠度曲线作为研究对象，计算结果见图5及表2所示。结构特征点荷载包括底板屈服荷载、顶板屈服荷载和极限荷载，其中极限荷载是指当结构或结构某一部位的节点发生过大位移或变形，导致计算结果不收敛时，对应的最大荷载。钢箱内是否灌注混凝土(即B-1与B-2)比较结果：

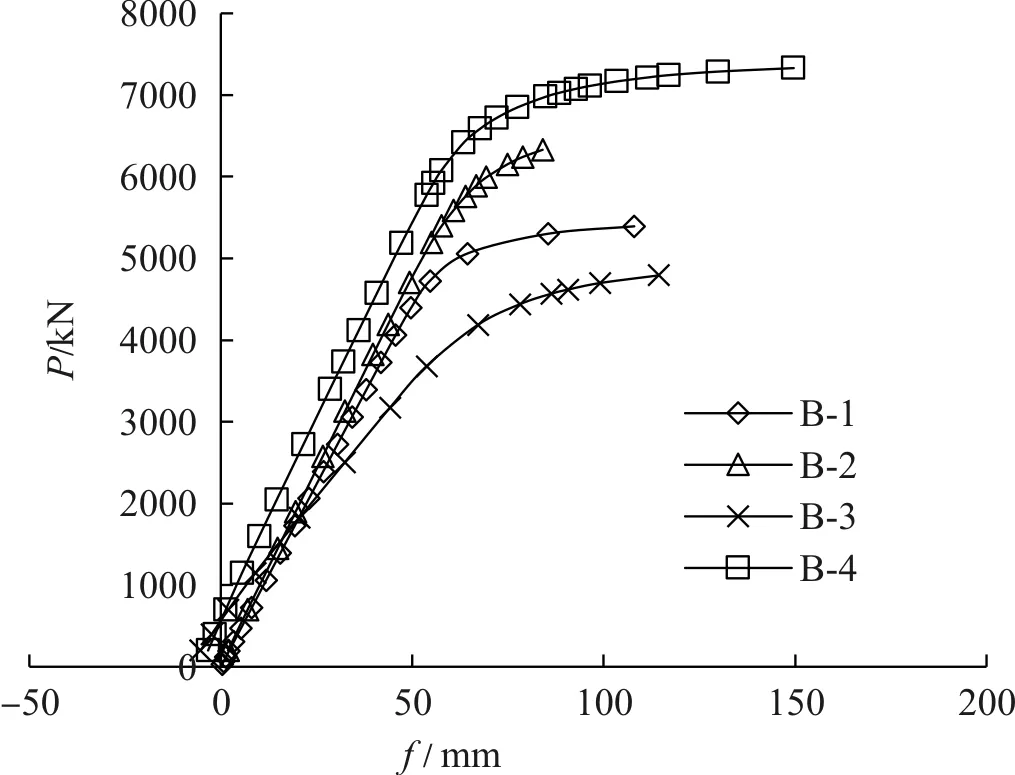
图5 B-1～B-4截面梁体的荷载位移曲线

(1)B-1顶板屈服荷载仅为B-2的40 %，表明钢箱内灌注混凝土参与受压从而有效地提高了结构顶板屈服荷载。

(2)二者底板屈服荷载相差较小，说明钢箱内灌注混凝土对于底板屈服的帮助不大。

(3)钢箱内灌注混凝土使得结构极限承载能力能提升约20 %。

B-2与B-4对比可知，张拉预应力筋能使结构底板屈服荷载提升13 %左右，同时能使结构承载能力提升15 %左右，结构刚度明显提升。

B-3与B-4对比可知，与矩形预应力钢箱梁混凝土相比较，设置宽翼缘板的双腹板工字型钢箱预应力混凝土的截面能够提高结构承载能力50 %以上，效果明显。

由以上比较可知，双腹板工字形钢箱预应力混凝土梁具有承载能力高、刚度大的特点，可应用于盖梁结构。

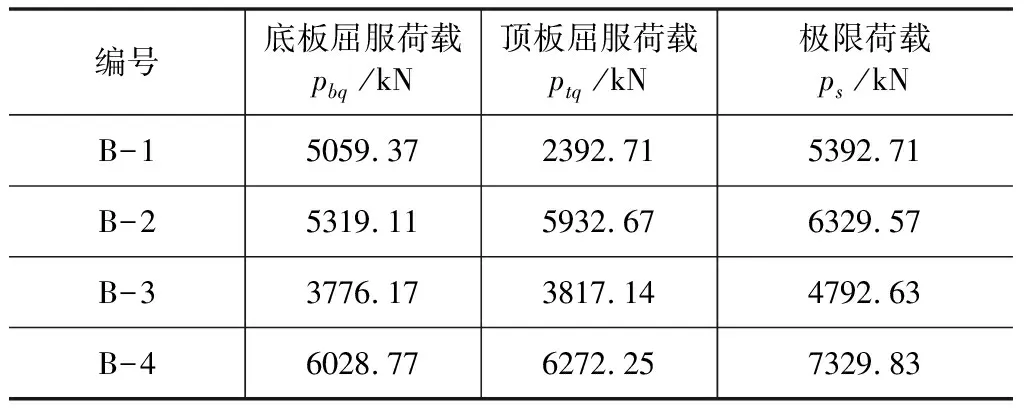
表2 结构特征点荷载 kN

3.3 双腹板工字形预应力钢箱混凝土梁的受弯力学行为

进一步分析，双腹板工字形预应力钢箱混凝土梁的结构破坏均经历了弹性阶段、屈服阶段和破坏阶段三个阶段。由图5中可以知：在弹性阶段，荷载与位移呈线性关系；在弹塑性阶段，受拉区混凝土开裂增多，底板先屈服，而后顶板开始屈服；在破坏阶段，即荷载接近极限荷载时，结构整体位移发展较快，曲线斜率趋势平缓。

结构接近破坏时的Von Mises应力分布见图6所示。随着荷载增大，结构在接近破坏时，混凝土开裂严重，荷载主要由钢箱承担，且结构顶板、底板均已屈服，但屈服区域较小，结构仍然具有继续承载的能力。受拉预应力筋在破坏阶段的最大应力为1 475.1 MPa，远小于1 860 MPa的极限应力，可认为结构接近承载能力极限时，预应力筋不会被破坏，能够继续承载并提供抵抗变形的能力，提升结构延性；从图5的B-4曲线可以看出，模型接近计算结束时，构件的跨中最大挠度接近150 mm，接近跨度的1/100，说明结构屈服后仍然具有较大继续承载能力，证明结构整体亦具有较大的延性，对于地震作用具有较强抵抗能力，适用于地震多发区域的桥梁建设应用。