大跨度混凝土楼板的自振频率分析
2018-09-14陈军武
范 康,陈军武
(中国有色金属工业西安勘察设计研究院,陕西西安 710055)
基于现代结构理论的发展和人们居住要求的提升,大跨度混凝土楼板在新建的民用建筑中较为普遍的出现。大跨度楼板可以使房屋功能划分更加自由,更加符合精细化设计。为了保证房间内人员的感官需求和建筑经济性,通常楼层高度被严格控制。采用次梁划分楼板难以满足要求,大跨度混凝土楼板成为一种选择。
混凝土楼板设计采用以概率论为基础的极限状态设计方法,包括承载能力极限状态和正常使用极限状态。而楼板舒适度问题在大跨度楼板设计中显得尤为重要,甚至起控制作用。在设计开始时必须确定振动源、振动传播路径(质量、刚度、阻尼)等因素和人们对于振动可接受的范围。民用建筑较多出现的振动源,如住宅内人的行、走、跳跃和健身器械的振动,公共建筑中清扫设备的振动,水平运输设备的振动等,在设计开始时就需要对这些问题仔细考虑[1]。
楼板的自振频率是结构的固有特性,大跨度混凝土楼板的振动主要表现为一阶竖向振动,当楼板自振频率较低,并与人的各种类型的活动频率比较接近时,容易引起共振,会使人感到不舒服和不安全[2][3]。本文基于板壳振动理论和已有的研究成果,结合SAP2000有限元分析软件对大跨度混凝土楼板自振频率的分析比较,可为大跨度混凝土楼板设计提供参考。
1 板壳振动理论及自振频率计算
楼板振动的关键参数主要是楼板的固有频率和相应的峰值加速度,楼板竖向自振频率属于结构的固有属性,竖向振动也是一种弹性体振动。由于楼板厚度一般远远小于其自身尺寸,可采用弹性薄板振动理论来分析楼板的自振频率。
计算方法是建立在薄板振动基本微分方程的基础上,研究薄板的固有振动问题;是考虑封闭的不同边界条件下,均匀厚度的矩形板的第一模态振型固有频率公式简化方法。本文主要以四边简支大跨度混凝土楼板为研究对象。
四边简支矩形板固有频率可按式(1)、式(2)计算[4]:
(1)
(2)
式中:频率系数λ与楼板边界条件及长宽比a/b有关,与板的材料常数无关,可按表1查出。
板的抗弯刚度D可按式(3)计算:
(3)
式中:E为材料弹性模量;ν为材料泊松比;h为板厚。

表1 四边简支矩形板频率系数λ值
研究表明,造成大多数振动问题的主要因素是共振,在人类的日常中,活动的频率主要介于2~3 Hz[4][5]。因此,设计中控制楼板的频率,避免楼板固有频率与人的活动频率相近,从而达到舒适度要求。
关于自振频率的控制要求,国内外已提出了一些具体要求。我国GB 50010-2010《混凝土结构设计规范》中要求住宅和公寓不低于5 Hz,办公楼和旅馆不宜低于4 Hz,大跨度公共建筑不宜低于3 Hz。加拿大国家建筑规范(NBC) 要求楼板自振频率不低于6 Hz[6]。其他类似的一些研究和要求均有一定的差异,设计中主要考虑在满足现有国家标准的基础上,对具体的设计采用更加合理的控制要求。
2 混凝土楼板自振频率计算与分析
2.1 基于板壳振动理论的简化计算
计算楼板采用C35混凝土,弹性模量E=3.15×104N/mm2,混凝土泊松比ν=0.2,钢筋混凝土的密度ρ=25 kN/m3。
(4)
将上述参数代入式(4)、式(1),可以得到:
当楼板尺寸为6 m×6 m时,f=0.028 3h,h为楼板厚度(mm)。
当楼板尺寸为9 m×6 m时,f=0.020 4h,h为楼板厚度(mm)。
当楼板尺寸为9 m×9 m时,f=0.012 6h,h为楼板厚度(mm)。
根据式(1)、式(4)及上述结果,三种尺寸规格的混凝土楼板的自振频率计算结果详见表2。
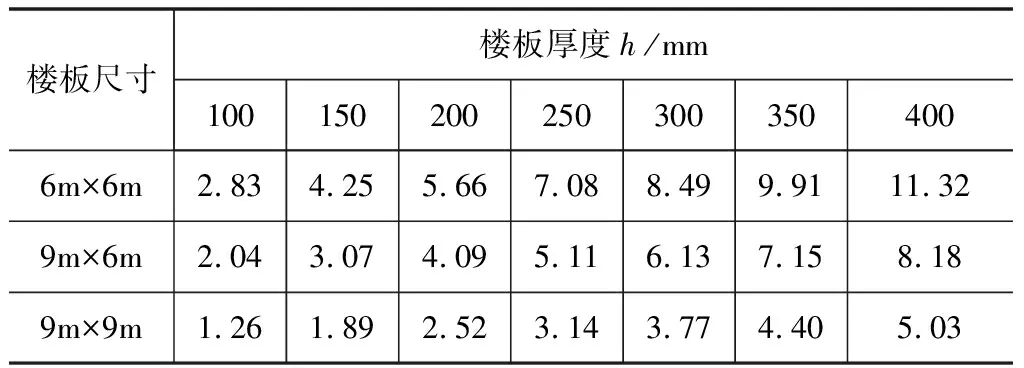
表2 基于板壳振动理论计算的楼板频率f Hz
2.2 采用SAP2000有限元分析软件对楼板频率的分析
采用SAP2000有限元分析软件对6 m×6 m,9 m×6 m,9 m×9 m三种模型进行自振频率分析,材料参数同上,分别对不同厚度的楼板进行模态分析。研究结果表明,人行荷载激励下,楼盖结构第1振型的振动分量起控制作用,高阶振型的影响并不显著[1]。分析结果见表3。
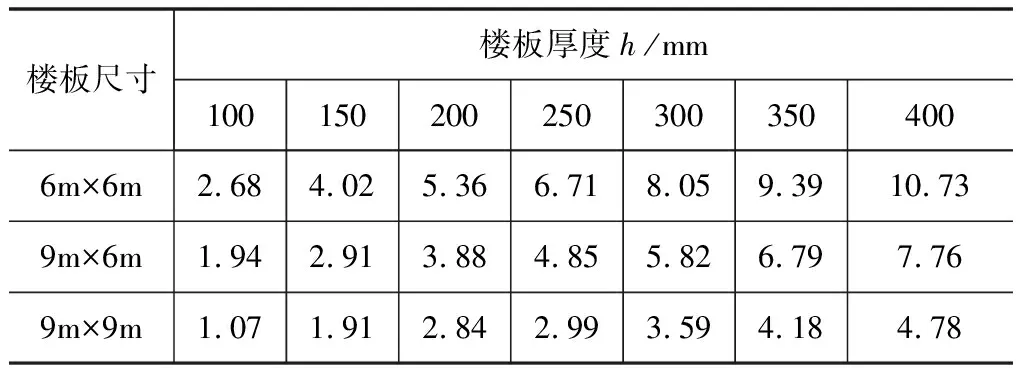
表3 基于SAP2000有限元分析的楼板频率f Hz
2.3 楼板厚度对自振频率的影响
结合表2和表3的结果,可以得到不同跨度楼板振动频率f与楼板厚度h之间的变化关系图,如图1所示。由图1可以得出:
(1)对于同一跨度楼板,基于板壳振动理论所计算的楼板自振频率f与楼板厚度h基本呈线性关系,随着板厚的增加,自振频率也不断增大。同时随着楼板跨度的增大,线性比例降低,即随着楼板跨度的增大,增加板厚对楼板自振频率的正面影响不断降低。
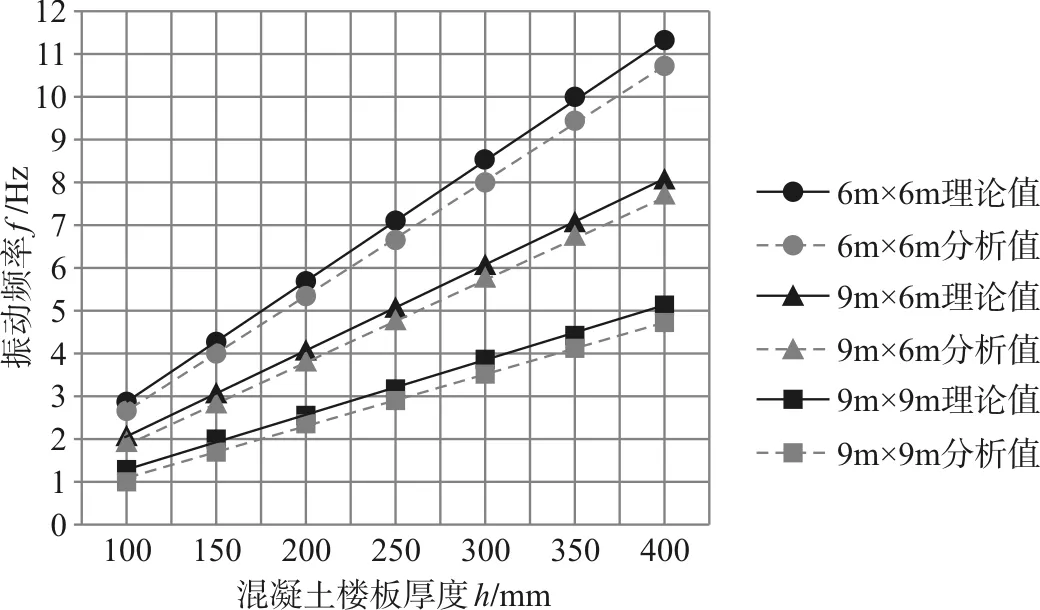
图1 不同跨度楼板振动频率f与板厚h的关系
(2)通过SAP2000有限元分析软件对三种模型的分析来看,其结果与板壳振动理论计算的结果基本一致,误差在5.5 %以内,楼板自振频率f与楼板厚度h也基本呈线性关系。板壳振动理论在研究分析薄板的固有振动频率方面较为合理。
(3)楼板长宽比a/b对楼板自振频率f有明显影响,其影响主要反应在频率系数λ,见表1。楼板长宽比为a/b的矩形楼板自振频率介于跨度分别为a、b的方板之间。
3 结束语
基于板壳振动理论,采用弹性薄板振动理论来分析楼板的固有频率,结合SAP2000分析软件对不同跨度楼板自振特性的对比分析,可以得出这是一种较为合理的方法。在设计前期可以帮助设计人员选用合理板厚及结构方案。
楼板固有振动频率随着板厚的增加也随之增大,基本呈线性关系。随着楼板跨度的增大,板厚对固有频率的影响减弱。考虑不同使用功能,楼板自振频率的控制要求也不同,需要综合考虑结构方案。
