钢结构轴心压杆稳定性简析
2018-09-14卢启财赵敬义罗光龙
卢启财,赵敬义,罗光龙
((1.济南历下控股集团有限公司,山东济南 250000;2.中国建筑西南设计研究院有限公司,四川成都 610042))
改革开放以来,随着经济突飞猛进的发展,钢结构以其轻质高强,抗震性能好、工业化程度高、工期短等独特的优势得到了前所未有的发展。可以说钢结构已经成为当前社会建设的必需品,有着不可替代的作用。
钢结构与传统钢筋混凝土结构相比,由于强度比混凝土构件大很多,为了充分发挥钢材的强度,提高截面效率,一般在设计钢结构时,其截面轮廓较小,构件相对细长。然而,如果对于轴心受压的钢构件处理不当,就很有可能发生失稳的现象(图1~图4),给人民的生命财产带来巨大的损失。因此,钢结构也有其不可忽视的缺点:结构的刚度小,稳定问题突出。

图1 某厂房屋架杆发生弯扭失稳

图2 加拿大魁北克大桥钢结构失稳事故

图3 某房屋受压斜杆发生弯曲失稳

图4 某厂房底层钢结构柱失稳造成整体坍塌事故
1 结构失稳破坏的定义
结构失稳破坏是指作用在结构上的外荷载尚未达到按强度计算得到的结构强度荷载时,结构已不能承担较大的变形,整个结构偏离原来的平衡位置而破坏或倒塌[2]。也就是说,结构的强度还没完全发挥,就破坏啦,强度不起控制作用。钢结构在失稳的过程中,变形会发生迅速增长,结构将在很短的时间内破坏甚至坍塌,呈现明显的脆性破坏。钢结构稳定性破坏的突发性,容不得人们有反应和撤离时间,造成的危害和损失是巨大和惨痛的!然而在另一方面,由于建筑效果的限制,材料和施工的缺陷等原因,钢结构大多发生的还是稳定破坏,所以验算钢结构的稳定性是非常重要的!
2 轴心压杆稳定性的理解和计算
轴心受力构件在钢结构中应用非常广泛,如桁架、网架中的杆件,工业厂房及高层钢结构的支撑,操作平台和其它结构的支柱等。除了一些较短的轴心受压构件因局部有空洞削弱,需要验算净截面强度外,一般情况,轴心受力构件的承载力是由稳定条件决定的。
对于理想的轴心压杆的整体稳定性问题,欧拉(Euler)早在18世纪就对其进行了研究。采用的是“理想压杆模型”,即假定杆件实等截面直杆,压力作用线与界面的形心纵轴重合,材料是完全均匀和弹性的,并得到了著名的欧拉公式。
(1)
式中:NE为欧拉临界力;E为材料的弹性模量;A为压杆的毛截面面积;λ为压杆的长细比。
由欧拉公式(1)可知,我们可以通过控制压杆的长度,加大压杆构件截面,来增大压杆的临界压力NE,保证不发生稳定破坏。
当然,实际工程中影响轴心压杆结构的稳定性的因素很多,如构件的初弯曲、初扭曲,荷载作用的初偏心,制作引起的残余应力,材性的不均匀等等。这些初始缺陷使得轴心压杆一开始就会出现弯曲变形,压杆的失稳也就成为了极值型失稳.因此实际的轴心压杆的稳定极限承载力不再是长细比λ的唯一函数。但是,影响其稳定性的主要的、也是设计人员可控的因素还是构件的长细比λ[2]。
GB 50017-2003《钢结构设计规范》(下面简称《钢规》)中,对于轴心压杆的稳定计算公式如下:
(2)[1]
式中:N为轴心压力;A为构件的毛截面面积;φ为轴心压杆的稳定系数(取截面两主轴稳定系数的较小者);f为钢材的强度设计值。
从公式2可以看出,对于单根受压杆件,其相比于强度计算公式,稳定计算公式多了轴心压杆稳定系数φ。轴心压杆的稳定系数φ是稳定性理论和统计分析结果在公式中的集中体现,达到了极简和实用的目的。稳定系数φ的计算也是轴心压杆稳定验算的难点和关键。其计算方法和步骤,笔者总结归纳如下:
(1)对双轴对称截面:
第一步:确定构件截面类型(a,b,c,d),通过查《钢规》表5.1.2.1-1和表5.1.2.1-2;需要注意的是《钢规》表5.1.2.1-1是对于厚度小于40 mm的构件而言,而《钢规》表5.1.2.1-2是对于厚度大于或等于40 mm的构件而言。
第二步:计算截面的回转半径ix和iy;
第三步:确定构件的计算长度lx和ly;
第五步:计算轴压稳定系数φ。有两种方法可选用。
其中:fy为材料的屈服强度。
当λn≤0.215时:φ=1-α1λn2;
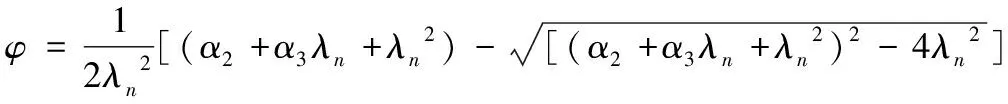
式中:α1、α2、α3按《钢规》表C-5查询得到。
(2)对于单轴对称的截面(比如T形钢),因为还可能发生绕对称轴方向的扭转失稳。故在计算绕对称轴的长细比时,须先经过公式(3)的处理,再用λyz代替λy[1]
(3)[1]
(4)[1]
i02=e02+ix2+iy2
(5)[1]
式中:e0为截面形心至剪心的距离;i0为截面对剪心的极回转半径;λy为构件对对称轴的长细比;λz为扭转屈曲换算长细比;It为毛截面扭转惯性矩;Iw为毛截面扇性惯性矩;对T形截面(轧制、双板焊接、双角钢组合)、十字形截面和角形截面可近似取Iw=0;A为毛截面面积;lw为扭转屈曲的计算长度。
(3)由于截面的不同,轴心压杆的失稳状态主要呈现三种,分别为弯曲失稳,如双轴对称的工字钢截面(图5);弯扭失稳,如单轴对称的T形截面(图6);和扭转失稳,如双轴对称的十字形截面(图7)。
三种失稳的状态对应的临界压力的计算方法也不尽相同,对应的临界压力值也是相差很大。因此,在设计轴心压杆的时候,应特别注意截面的选择。
比如某轴心受压实腹杆件,轴心压力设计值(包括构件自重)N=1 500 kN,计算长度lx=ly=3m;拟采用Q345B钢材,我们分别选用同样截面面积的焊接组合工字形钢(翼缘钢板为火焰切割边)(图8)与焊接T型钢(图9),并对比两者在荷载作用下稳定应力的大小。
当采用图8所示焊接组合工字形钢(翼缘钢板为火焰切割边)时,查《钢规》表5.1.2.1-1可知截面为b类截面,且截面参数如下:
截面面积A=25×1.2×2+25×0.8=80 cm2
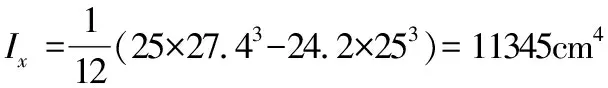

图5 弯曲失稳示意

图6 弯扭失稳示意

图7 扭转失稳示意

图8 焊接组合工字形钢截面
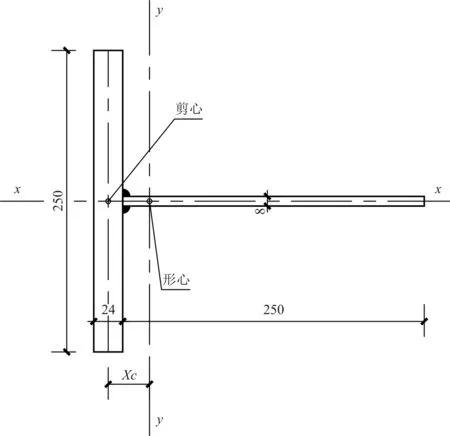
图9 焊接T型钢截面
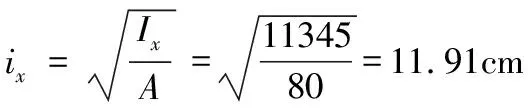
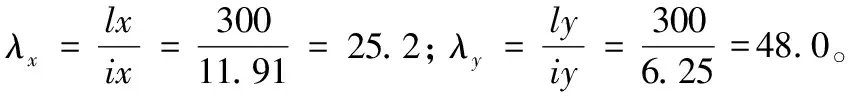
b类截面,按《钢规》表C-5,查得α1=0.65、α2=0.965、α3=0.30,
计算轴心压杆稳定系数φ:
=0.8169
根据公式2,计算得到压杆稳定应力:
(b)当采用图9所示焊接T形截面时,查《钢规》表5.1.2.1-1可知截面对x轴为C类截面,对y轴为b类截面且截面参数如下:
截面面积:A=25×2.4+25×0.8=80cm2
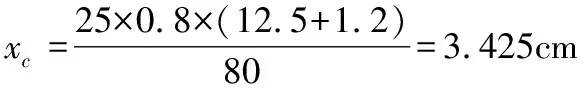
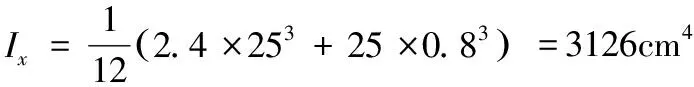
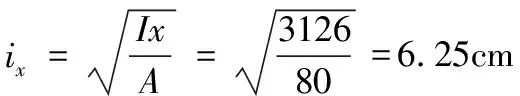
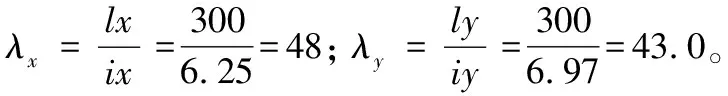
T形截面的剪力中心在翼缘板和腹板中心线的交点,所以截面形心至剪心的距离e0的距离等于xc,即:
e0=xc=3.425cm
截面对剪心的极回转半径:
i02=e02+ix2+iy=3.4252+6.252+6.972=99.38 cm2
对于T形截面,毛截面惯性矩:Iw=0;
扭转屈曲换算长细比:
则换算长细比:
=52.45
用λxz=52.45代替λx
由于绕x轴和绕y轴失稳的截面类型分别为c类和b类。故下面分别验算,以求得较大轴压稳定系数φ。
对x轴(c类):
求得正则化长细比:
计算稳定系数φ:
c类截面,且λn=0.6832≤1.05,按《钢规》表C-5,查得α1=0.73、α2=0.906、α3=0.595
=0.6852
对y轴(b类):
求得正则化长细比:
计算稳定系数φ:
b类截面,按《钢规》表C-5,查得α1=0.65、α2=0.965、α3=0.30
=0.8466
φ取φx和φy的较小值,即:φ=φx=0.6852
根据公式(2),计算得到压杆稳定应力:
通过上述实例验算可知:相同荷载作用下的轴心压杆,截面面积相同的工字钢和T形钢的稳定应力分别为229.5 Mpa左右和273.6 Mpa,两者相差44.1 Mpa!故双轴对称的工字钢比单轴对称的T形钢的整体稳定性能更好!
3 结束语
钢结构应用普遍,稳定性问题突出。既和钢材的缺陷、施工的质量相关,更与设计人员的稳定性概念和意识相关。对轴心受压,一方面,应适宜的控制构件的长细比;另一方面,应尽量采用双轴对称的截面,以达到安全可靠,经济合理的目标。
