基于Monte-Carlo随机数法的横山滑坡稳定性可靠度分析

赵海鑫

(西南交通大学土木工程学院，四川成都 610031)

在对滑坡进行研究和治理的过程中，滑坡稳定性分析是关键问题之一[1]。目前为止，滑坡稳定性评价方法可概括为以下三种常用方法：(1)采用极限平衡状态分析的安全系数评价方法；(2)采用数值模拟分析的数值计算方法；(3)采用非线性数学、信息类科学、仿生学等新学科交叉方法的新型评价方法[2]。本文采用从随机分布概率出发的可靠度分析法，考虑了岩土体参数存在的变异特征，评价滑坡稳定状况。基于Monte-Carlo随机数法，建立对应Monte-Carlo随机表示过程，求解滑坡失效概率和可靠度指标，充分分析了可靠度理论分析滑坡稳定性的优势和适用性，并对G4216线横山滑坡稳定状况进行综合评价。最后，综合横山滑坡稳定性状态，为该滑坡防治研究提供技术参考。

1 滑坡稳定性可靠指标程序编制

Monte-Carlo法(简称M-C法)是运用随机技巧的统计模拟法,又称随机技巧法或统计模拟法，其理论基础是概率论中的大数定律[3]。在目前结构可靠度的计算中,它被认为是一种相对精确的计算方法。用“M-C”法求解结构的可靠指标,为了得到满足一定精度的相对精确解,须解决以下两个问题:(1)随机变量的抽取;(2)抽样次数必须满足最低抽样次数的要求。一般说来,最低的抽样次数须满足:N≥100/Pf本文采用蒙特卡罗方法求解滑坡稳定性可靠指标,具体程序框图如图1所示。

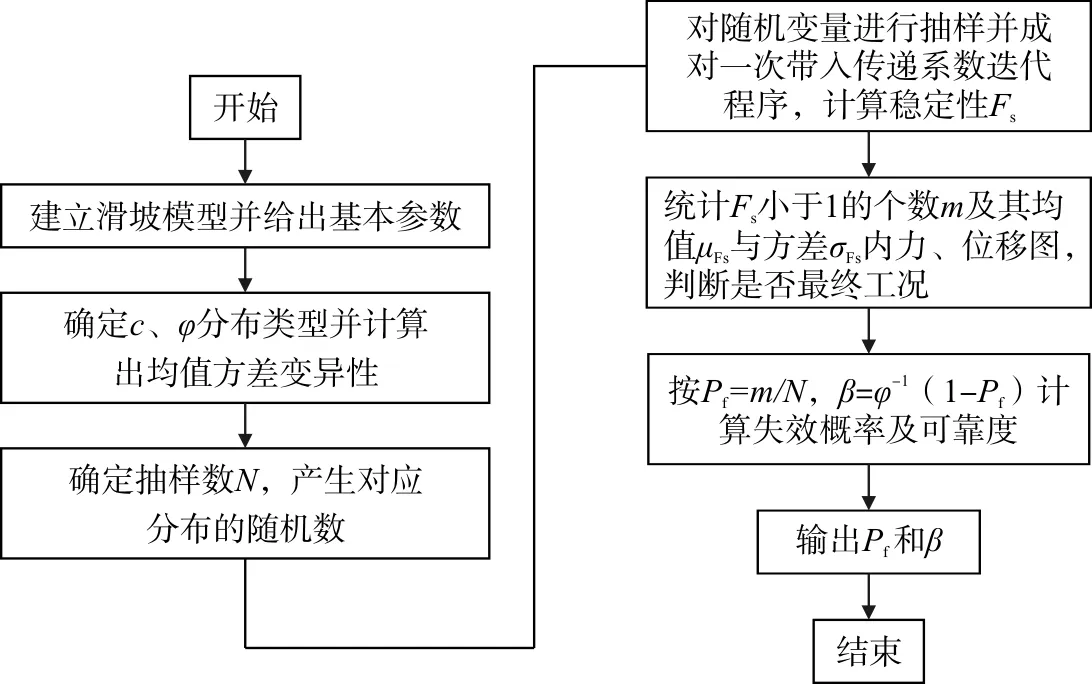
图1 传递系数法计算滑坡可靠度流程

2 计算实例及分析

本文以G4216线仁寿经沐川至新市(含马边支线)高速公路LK40+100横山滑坡作为工程实例进行可靠度分析。

2.1 滑坡概况

本滑坡处于马边县劳动乡红朱院，滑坡所在斜坡坡向290-10°左右，滑坡滑体后部最高点高程约640 m，前缘最低点约540 m，滑体相对高差约100 m，滑体纵向长约440 m，宽约500 m，滑体整体坡度15°～25°，呈三级坡度的折线型斜坡，上下平均坡度16°～25°，中部平台坡度0°～5°，坡体上被垦为旱地或水田，坡体上坳沟及缓坡平台发育(图2)。

图2 滑坡分区示意

根据滑坡体地表地形差异及钻探揭示物质组成情况，可将整个滑坡体划分为一个大区(I)和两个亚区(I1和I2)，整个滑坡体编为I区，北东侧次级滑体编为I1，I1亚区又包括一个次亚区I11，南西侧次级滑体编为I2区。

I区即为整个滑坡体，通过现场调查访问发现，本滑坡后壁及周界较清楚。后壁为砂岩顺层层面坡(光石板)，石板以上斜坡为林地，未见有滑坡迹象；滑体北东侧边界为陡坎，陡坎下基岩出露，边界清楚；滑体南侧与正常斜坡之间有一明显地形变化界线，形成斜坡冲沟形态，与正常坡体分界，且在分界线附近发育串珠状土洞，整个滑坡体呈扇形向北西向凸出，形态明显。

在I区北东侧边界附近发育次级滑体I1，该次级滑体纵向长约240 m，横向均宽约100 m，滑坡地形明显，呈一沟槽形状，滑体高程比周界高程低5～10 m，横断面呈浅碟状，错台等坡体滑动痕迹仍依稀可见。该次级滑体前缘还发育了一个次级滑体I11，该滑体即鱼塘周边滑体，纵向长约120 m，横向均宽80 m，其滑体比I1滑体低1～5 m，呈圈椅状地形。约20年之前，该部分滑体后部发生过滑动，但整体未发现过失稳。目前，该滑体上建有一鱼塘，塘水深2～3 m，该塘目前已干涸。

I区南西侧次级滑体为I2滑体，该滑体前后长166 m，横向均宽200 m，地形上呈一扇贝形，滑体前部微凸出，周界与I区滑体地形分界明显。该次级滑体后部有一陡坎，坎高5～8 m，与I区主滑体分界。据钻孔揭示的卵石分析，该次级滑体滑下后覆盖在马边河阶地之上，目前整体处于稳定状态，但前缘临空部分有少量垮塌。

根据钻探揭示，滑坡具有典型的顺层基岩滑坡特征，部分钻孔揭示的块石呈整体状，即块石间未发生过相对滚动位移，但裂隙发育，且有张开1～200 cm的裂隙，充填含角砾粉质黏土。钻探揭示的块石含量及块石完整性与地形能较好的对应，即钻孔内揭示的块石完整或含块石量高，则地形上呈现凸出的正地形形态，钻孔内揭示的块石含量低或为含角砾粉质黏土的地形则呈现出凹陷的负地形，I1、I2两区次级滑体内岩体完整性相对差，黏性土含量相对较高。

部分钻孔中还揭示，在岩土界面上3～5 m范围内，密集发育有多处光滑面，光滑面倾角15°～50°皆有，光滑面上附少量黏土，部分已高岭土化，呈灰白色，粘性强，可塑性强。在岩土界面以下3～10 m范围内的滑床岩体受上覆滑体的挤压、搓动，完整性也很差，裂隙发育，但一般未见到光滑面。而且滑体中后部，即滑面(带)较陡的部分的滑床岩体扰动带岩体完整程度要好于滑体中前部，即滑面(带)较缓部分，表现出了滑体在中后部对滑床岩体的扰动要弱于中前部的特点，符合顺层基岩滑坡的特点。

2.2 Monte-Carlo法模拟横山滑坡稳定性可靠度

在计算横山滑坡可靠度时，采用MATLAB自带的函数工具箱可以很快的进行随机数的产生以及图形的绘制。通过对c和φ进行相应的处理后，随机获取1×106组数据所得c(对数正态分布)和φ(正态分布)值概率密度进而求得I区内Fs服从正态分布，均值为μⅠ=1.149 2，σⅠ=0.137 3，βⅠ=2.97；I1区内Fs服从正态分布，均值为μⅠ1=1.172 3，σⅠ1=0.145 8，βⅠ1=2.24；I2区内Fs服从正态分布，均值为μⅠ2=2.231 4，σⅠ2=0.132 4，βⅠ2=1.25。

本文参照祝玉学[4]提出的边坡工程目标可靠度2.321～2.748作为标准进行分析。该滑坡I区βⅠ=2.97>2.748处于稳定状态; I1区βⅠ1=2.24在2.321～2.748之间，可靠度较低；I2区βⅠ2=1.25<2.321，不可靠。

对比稳定系数反算值，I1区域在可靠度分析中，可靠度较低，而稳定系数认为该区域稳定，通过实地调查研究发现，该次级滑体滑动方向变化，在坡脚部分仍存在不稳定因素，且该滑体上形成了斜坡凹槽，利于雨水及周边地下水汇集，长期稳定性不能保证，需要进行监测并处治。

3 结论

本文详细介绍了基于Monte-Carlo随机数法计算滑坡稳定性可靠度的方法，并通过横山滑坡稳定性可靠度分析对该方法进行实例论证，主要得到以下结论：

(1)采用基于Monte-Carlo随机数法计算滑坡稳定性可靠度，弥补了极限平衡分析法没有充分考虑岩土参数变异性的不足，具有理论基础，且操作简便，适用性强。

(2)实例分析结果表明，极限平衡分析法所确定的滑坡稳定区域，在可靠性分析中可能为不稳定区域，采用极限平衡分析给出的安全系数取值和实际情况可能不相符，采用可靠度分析的方法为滑坡稳定性研究提供了更合理的依据。