第一类换元积分法的解构和重构
——兼简论一元积分学的改革
2018-09-13石德刚董春芳
石德刚,董春芳
(天津冶金职业技术学院,天津 300400)
一元积分学与一元微分学有着密切的联系,它们共同组成了高等数学的主要部分——微积分学.现行高等数学教材,将一元积分学分为不定积分与定积分及定积分的应用三部分。学生按照这样的学习材料组织顺序学习,不仅费时,而且学习时还会产生如:为什么要先学习不定积分(原函数)?引入原函数的意义是什么?一定要先学不定积分后学定积分吗?等诸多疑问。
在对比、剖析国内外多种同类教材的基础上,本文作者结合自己对一元积分学教学的研究心得,本着学生易学,教师易教的宗旨,对一元积分学知识体系进行解构和重构,依据典型学习任务有机地整合学习内容,减轻学生学习一元积分学的负担。简述如下:
通过求曲边梯形的面积和求变速直线运动的路程等实例,指出定积分与导数一样也是在解决一系列实际问题的过程中逐渐形成的数学概念.
通过阐明运用定积分定义通过求积分和的极限求定积分的值不仅是很麻烦的,而且有时是很困难的,甚至可能根本无法求得定积分的值,指出必须寻找一个具有普遍性且行之有效的计算定积分的方法,否则会影响定积分的实用价值.
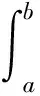
然后阐明牛顿和莱布尼茨证明了上面得出的结果具有一般性,并建立了下面的微积分基本公式:
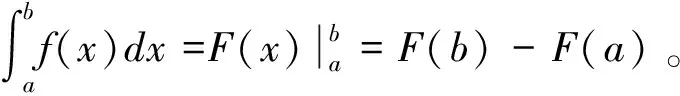
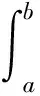
再进一步指出,鉴于牛顿—莱布尼茨公式中的函数F(x)对计算定积分的重要性,需依据函数F(x)的特性(F′(x)=f(x)),引入新概念——原函数(不定积分),从而将原本各自独立的积分与微分联系起来,使微分学与积分学成为一个统一的整体——微积分学.
依据各种积分法的实质,学习直接积分法、第一类换元积分法、分部积分法时,不分不定积分与定积分;学习第二类换元积分法时,阐明运用第二类换元积分法时不定积分与定积分的的区别。下面着重谈谈本文作者对第一类换元积分法所做的解构和重构。
第一类换元积分法(凑微分法)是一元积分学中求积分的最常用的重要方法。第一类换元积分法是将一元微分学中的复合函数微分法反过来用于求积分,是当被积表达式不容易求出积分时,通过恒等变形和变量代换,将被积表达式转化为基本积分公式表中的某一被积表达式,然后根据基本积分表中的某些公式,对新变量进行积分,最后还原求出结果.第一类换元积分法的关键步骤是“凑微分”,熟练掌握和运用“凑微分”的思想方法,对学习后续的第二类换元积分法和分部积分法等积分方法有着很重要的作用.
由于“凑微分”没有一个固定的模式,初学者在学习的过程中往往对要“凑微分”的函数作出多次尝试,因此第一类换元积分法是学生学习一元积分学时感到最难以掌握的积分方法。本文对第一类换元积分法的“凑微分”思想的理论依据进行解构和重构,总结出“凑微分”的具体方法。下面介绍作者的工作,并举例说明如何运用“凑微分”法求积分,以帮助初学者更好地学习和掌握“凑微分”法在积分运算中运用.
一、不定积分形式不变性
运用直接积分法,只能计算一些较简单的不定积分,因此必须进一步研究求不定积分的方法.积分法作为微分法的逆运算,与微分法中非常重要的复合函数微分法相对应,积分法中也有不仅要牢记而且必须熟练运用的换元积分法.
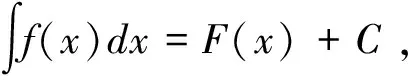

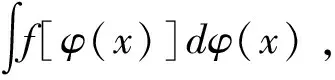
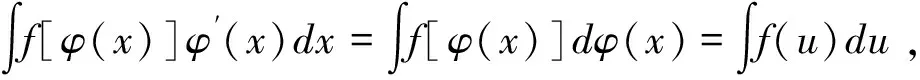
二、凑微分法的典型用法及常用凑微分公式
显然,恰当地选取函数φ(x)是运用凑微分法的关键,但是可导函数φ(x)有无穷多个,因此φ(x)的选取并无一定的规律可循.因为具体解题时只使用某些特殊的φ(x),所以在式(3)中,将可导函数φ(x)特殊化,即得一些常用的凑微分公式.
1. 在式(3)中,分别令φ(x)=Aarctanx+B(A≠0)、φ(x)=Aarccotx+B(A≠0)、φ(x)=Aarcsinx+B(A≠0)、φ(x)=Aarccosx+B(A≠0)整理得:
具体解题时,对所求不定积分,要先用式(4)或类似于式(4)的公式凑微分,然后再用式(2)类似式(2)的公式求不定积分.

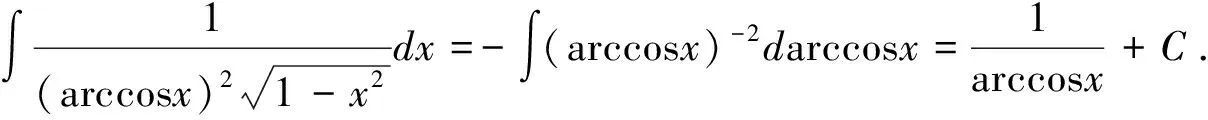
2.在式(3)中,分别令φ(x)=alnx+b(a≠0)、φ(x)=aex+b(a≠0),整理得:
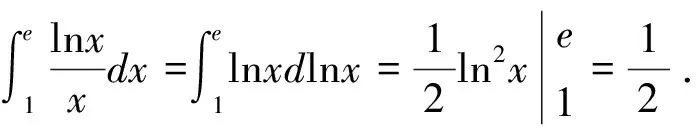
解
解
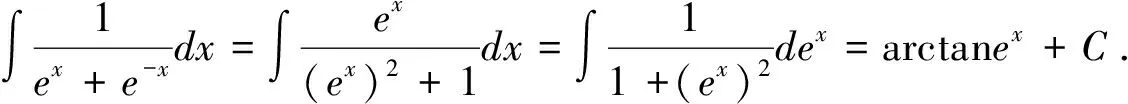
解
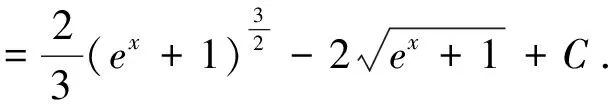
3.在式(3)中,令φ(x)=axn+b(a≠0),整理得:
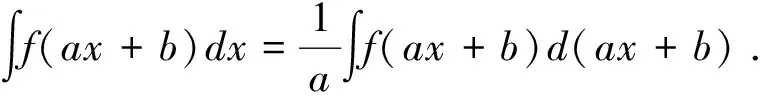
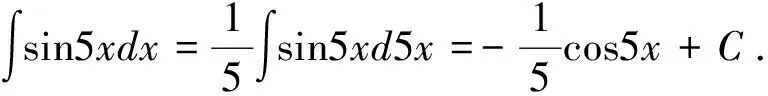
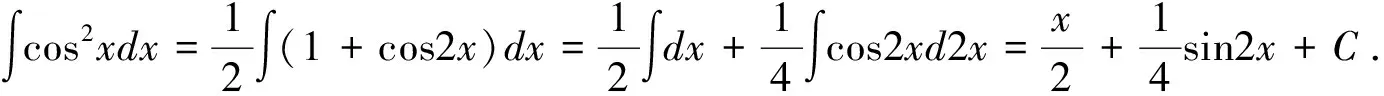
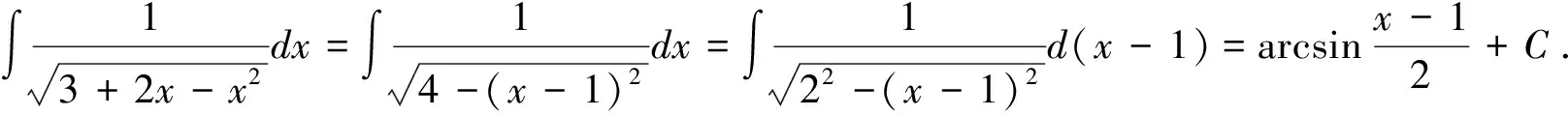
解
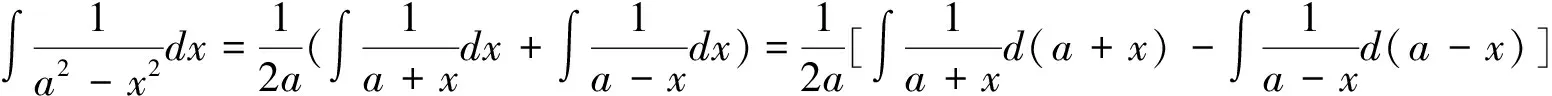
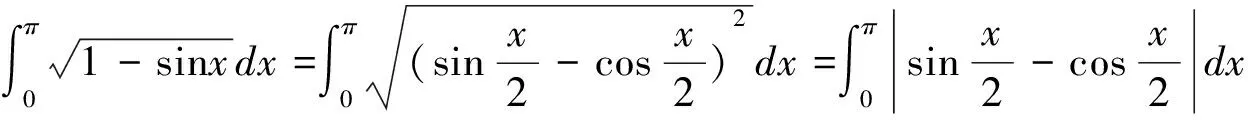
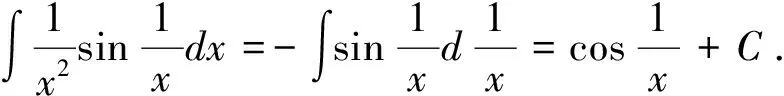
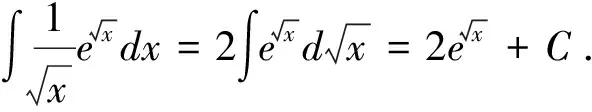
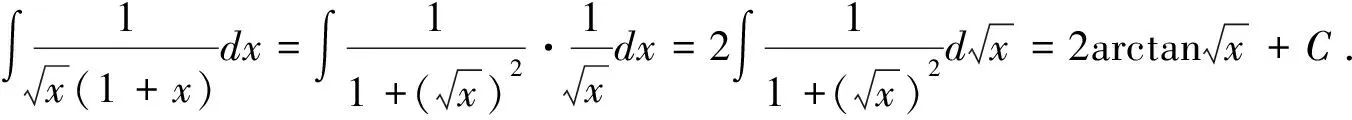
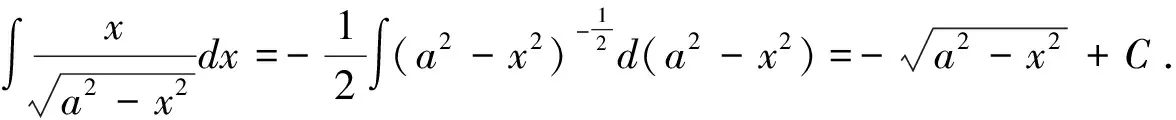
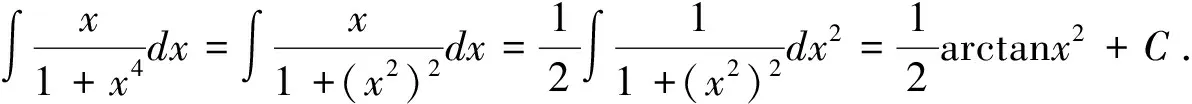
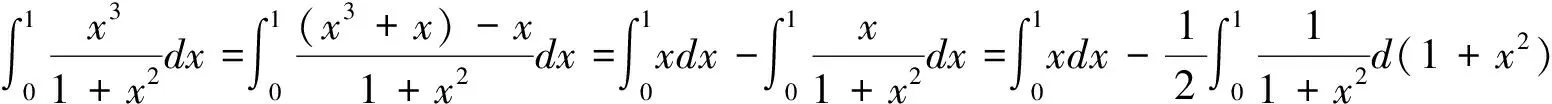
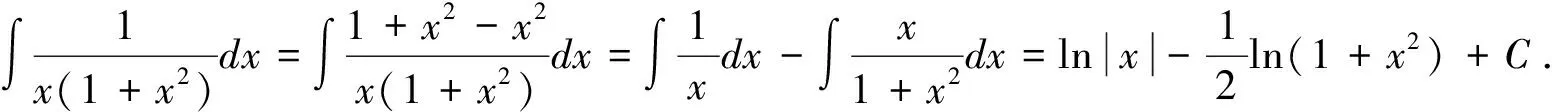
5.在式(3)中,分别令φ(x)=asinx+b(a≠0)、φ(x)=acosx+b(a≠0)、
φ(x)=atanx+b(a≠0)、φ(x)=acotx+b(a≠0),整理得:

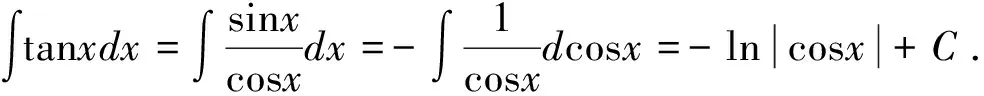

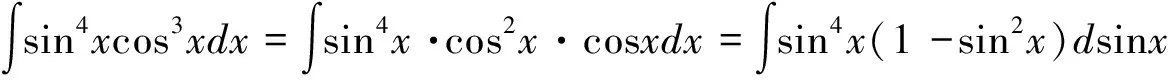
解
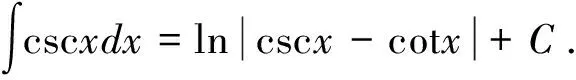
解
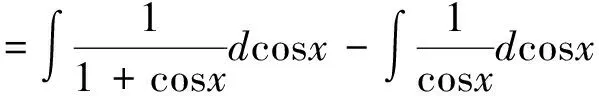
解

解
三、凑微分法的一般用法
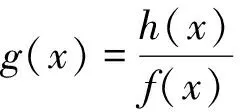
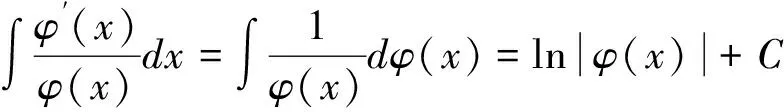
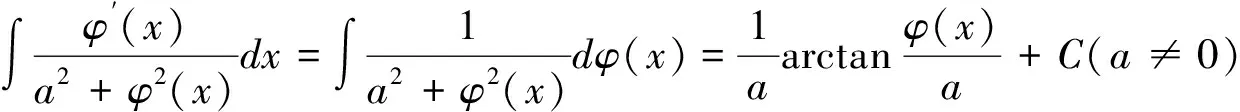
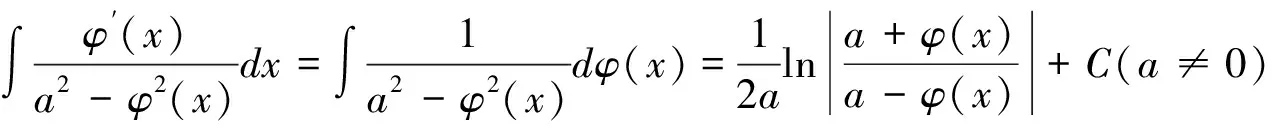
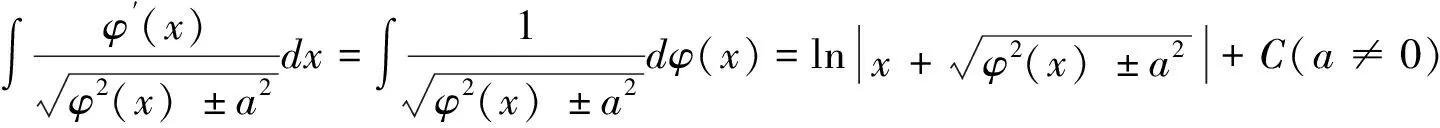
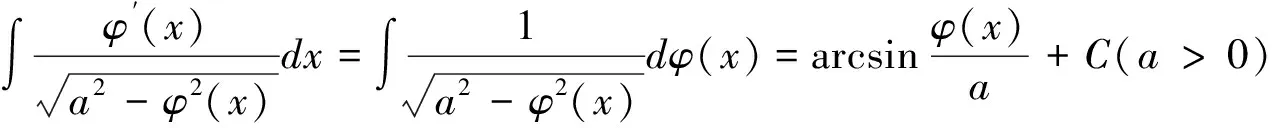
(2)当g(x)=f(x)h(x)时(假定f(x)比h(x)复杂),对f(x)或构成f(x)的初等函数求导,看其导数是否等于h(x)或h(x)的常数倍,若是则可以凑微分.本题型一般涉及以下凑微分公式(其中φ(x)是可导函数):

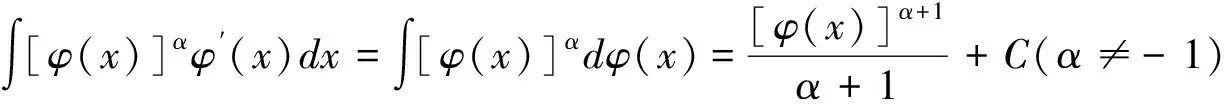
通常需要先对被积函数g(x)进行适当地变形处理后,才能按照(1)或(2)去做.
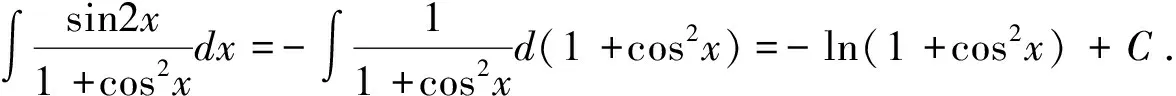


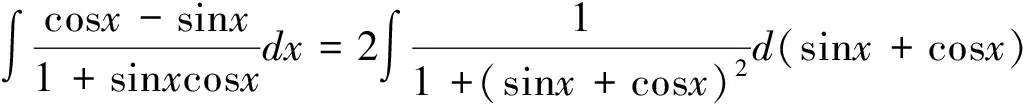
解
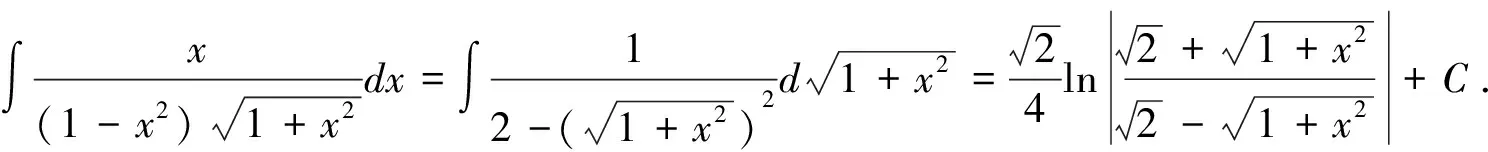
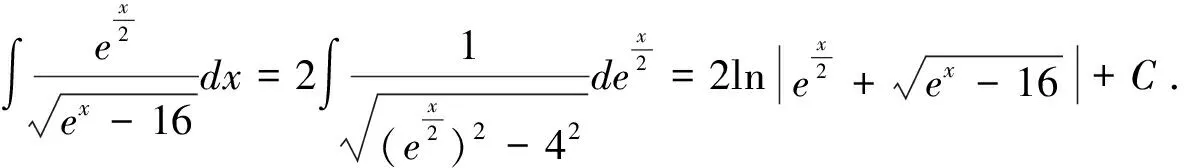
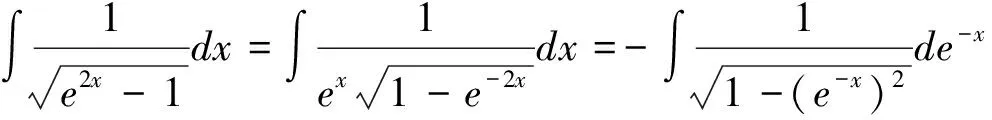
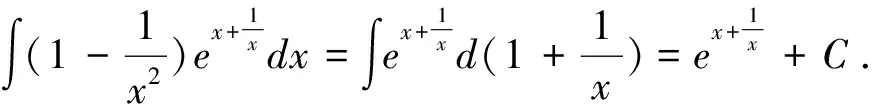
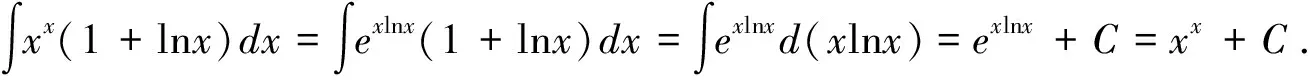
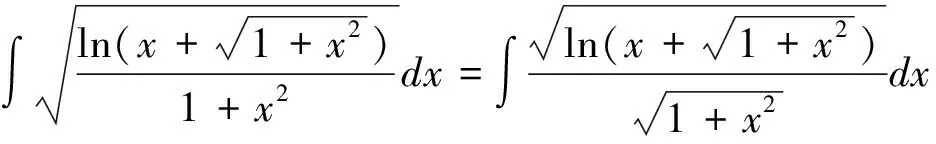
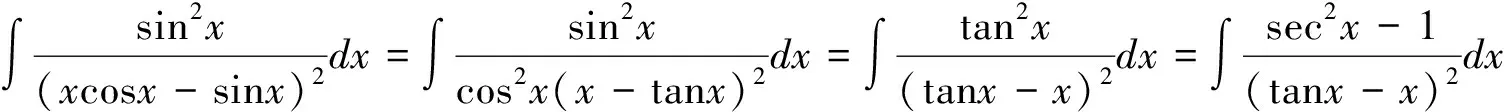
最后必须指出的是:要高效率地运用十分有效且应用广泛的凑微分法。要求首先,必须熟练掌握基本积分公式的广义形式(不定积分形式不变性表明,将基本积分公式中的积分变量换成可微函数后公式仍成立);其次,需要熟记常用的凑微分公式,以使被积表达式变形为,从而针对所要求的积分快速选准相应的基本积分公式的广义形式(凑微分法的目的就是将所要求的积分转化成能使用基本积分公式的广义形式);再者需要较多的掌握各种积分类型的特点,以及与之相适应的凑微分公式,同时需要在练习中随时注意被积函数的类型和特点,并体会转化被积函数的方法,这样才能增强观察的敏锐性和积淀成功的经验,从而提高用凑微分法准确、迅速求解不定积分的能力.
