一种基于相位差滤波过程的新型连续相位板设计方法
2018-09-12李福建
李福建

【摘 要】连续相位板是高强度激光系统束匀滑技术中的关键一环,其作用是改变激光聚焦焦斑的形态。基于Gerchberg-Saxton算法,本文提出了一种新的连续相位板设计方法,通过对相位差进行滤波,避免了传统设计方法中远场缓变的要求及复杂的解相过程,从而达到节约计算时间,简化编程的目的。同时通过控制相位差滤波参数,能够对所设计的连续相位板形态进行一定调控。
【关键词】束匀滑技术;连续相位板设计;G-S算法
中图分类号: P228.4 文献标识码: A 文章编号: 2095-2457(2018)13-0001-002
DOI:10.19694/j.cnki.issn2095-2457.2018.13.001
1 相位板设计简介
受控核聚变是人类解决能源问题的一大方向。为了利用聚变能,人们设计了不同类型的聚变装置,其中惯性约束核聚变由于其技术的可行性,一直被寄予重望。在激光驱动的惯性约束核聚变装置中,束匀滑装置必不可少。束匀滑技术是实现聚变燃料内爆过程的关键之一,对于控制激光等离子体作用影响很大。而束匀滑技术中,相位板的使用是焦斑形态的关键。相位板用于改变焦斑形态,自从随机相位板整型方法由Kato于1983年提出[1],相位板便被广泛应用于高强激光器中。而后人们又提出了相息相位板,连续相位板。根据光束传播的菲涅尔衍射理论,对于波长的光,用k表示其波矢,入射光场U(ξ,η)传播距离z后所得到的U(x, y)有如下表达式:
在经过透镜聚焦的情况下,有:
焦斑与入射场间通过傅里叶变换联系。所以在入射场函数U(ξ,η)上增加相位因子能改变焦斑形态。为了获得特定形态的焦斑,相位板分布需特殊设计。G-S算法[2]因其快速便捷的特点,被广泛应用,G-S算法由Gerchberg与Saxton于1972年提出。G-S算法设计获得的相位板存在不连续线,不连续线两边相位相差2。不连续线可以分为开环与闭环两种,闭环来自于算法中取相位值的步骤,可通过解相消除。而开环来自于近场场强奇点[3],无法消除。在高强度激光装置中,相位板的不连续点容易被高强激光损坏,同时不连续的边缘也会将小部分光折射至大角度,从而损失能量。连续相位板由Lin.Y于1996年提出[4],连续相位板(continuous phase plate,CPP)的使用避免了不连续结构,从而增大了能量利用率,延长了器件使用寿命。为了获得连续相位板,人们提出了一些相应的设计方法然而这些方法往往包括繁杂的解相位过程,效率较低。
2 相位差滤波CPP设计方法
2.1 相位差滤波CPP设计方法简介
相位差滤波CPP设计方法是一种新的改进G-S算法,与传统CPP算法相比,相位差滤波算法将滤波过程加在相位差上而不是相位上,由此避免了对相位滤波导致的相位分布大幅度变化,从而更容易达到收敛。给定入射场Ein,目标场Eout,其过程如下:
1.生成连续相位作为近场相位分布?渍1。其生成方法为对随机矩阵以宽度D1滤波后乘以幅度常数A1。
2.对近场分布Enf=Ein*exp(i*?渍1)作傅里叶变换,获得远场分布Eff。
3.对Eff卷积获得远场分布包络Eev。
4.通过比较远场包络与目标场分布,获得变换矩阵T=Eout/Eev。
5.在T上进行宽度为DT的滤波过程。
6.将T作用在远场分布Eff上,得到新的远场分布E。
7.对Eff作逆傅里叶变换,获得近场分布Enf。
8.取Enf的相位分布?渍2,求出在0-2?仔范围内的相位差?渍d=?渍2-?渍1。
9.对?渍d进行宽度为Dd的滤波得到?渍d,获得新的近场相位分布?渍1=?渍1+?渍d。
10.比较远场Eff与目标场Eout,如果远场没达到要求且迭代次数没达到限制次数,重复2-9步骤;反之,结束迭代,取?渍1为设计结果。
为了使用相位差滤波算法设计CPP,需要确定的参数有:Ein,Eout,D1,A1,DT,Dd。根据G-S算法的研究结果,A1选取为6?仔是合适的,所以固定A1为6?仔,选取Ein为充满采样区域的平面波,目标场为8阶超高斯分布,宽度为半采样宽度。
2.2 收敛特性
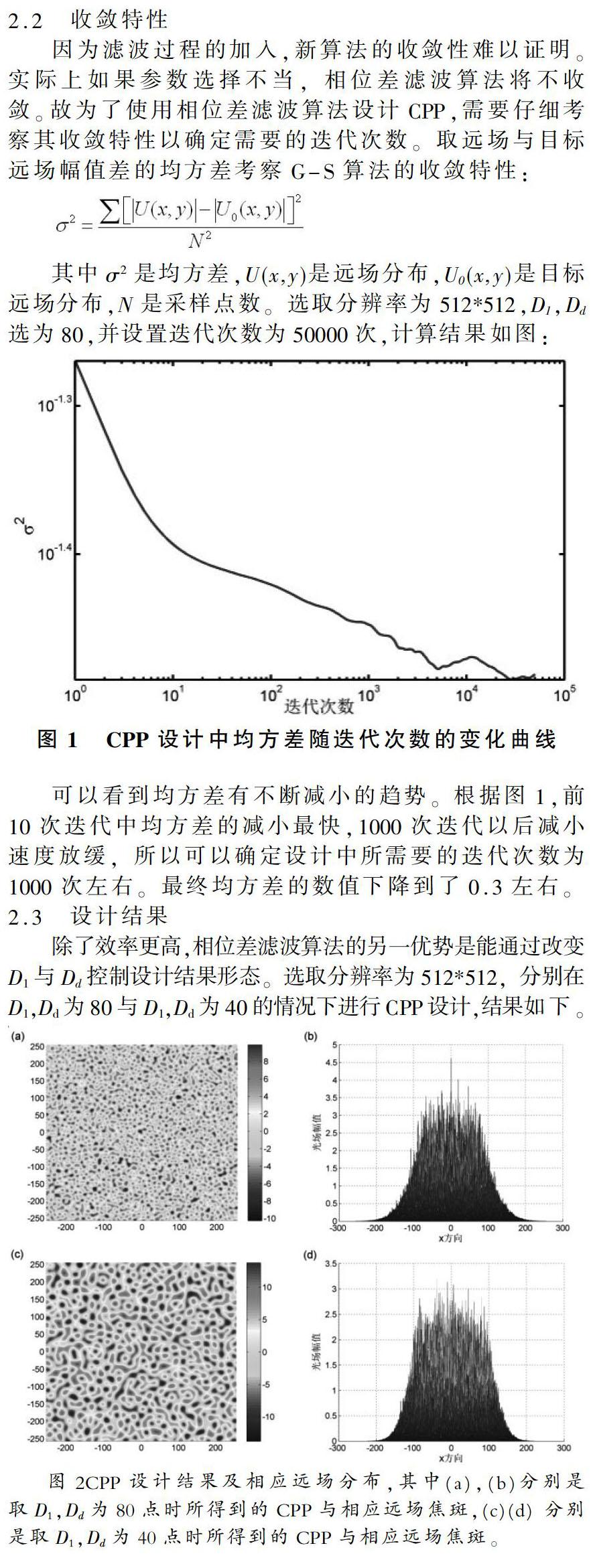
因为滤波过程的加入,新算法的收敛性难以证明。实际上如果参数选择不当,相位差滤波算法将不收敛。故为了使用相位差滤波算法设计CPP,需要仔细考察其收敛特性以确定需要的迭代次数。取远场与目标远场幅值差的均方差考察G-S算法的收斂特性:
可以看到均方差有不断减小的趋势。根据图1,前10次迭代中均方差的减小最快,1000次迭代以后减小速度放缓,所以可以确定设计中所需要的迭代次数为1000次左右。最终均方差的数值下降到了0.3左右。
2.3 设计结果
除了效率更高,相位差滤波算法的另一优势是能通过改变D1与Dd控制设计结果形态。选取分辨率为512*512,分别在D1,Dd为80与D1,Dd为40的情况下进行CPP设计,结果如下。
图2CPP设计结果及相应远场分布,其中(a),(b)分别是取D1,Dd为80点时所得到的CPP与相应远场焦斑,(c)(d)分别是取D1,Dd为40点时所得到的CPP与相应远场焦斑。
可以看到新算法对相位分布形态控制的有效性:通过调整初始相位及滤波宽度,可以控制相位板的变化频率。然而进一步降低D1,Dd到10时,远场分布与目标分布出现了较大的偏差,存在明显背景噪声。此时获得的CPP局部最大相位达到了40弧度。事实上滤波参数是不能随意降低的,为了获得目标分布,光场必须具有一定空间频率范围,这可以通过不确定原理来理解:近场光场频率的宽度与远场强度分布的宽度不能同时任意缩小,而CPP设计中,远场强度分布宽度是确定的,所以必然存在一个近场光场频率宽度的最小值,如果选择滤波参数小于此数值,设计结果必然出现背景噪声以扩大远场强度分布宽度。
3 結论
本文提出了一种相位差滤波算法,用于设计高强激光系统中光束整形使用的连续相位板。这种新方法由于避免了传统算法中复杂的解相过程而有着较高的效率。同时可以通过选择不同的滤波参数直接对设计的CPP形态进行控制。计算结果显示,此算法设计的相位板远场形态与目标函数接近,没有背景噪声,达到了焦斑整形的要求。
【参考文献】
[1]Y.Kato,K.Mima,N.Miyanaga,S.Arinaga,Y.Kitagawa,M.Nakatsuka,and C.Yamanaka, "Random Phasing of High-Power Lasers for Uniform Target Acceleration and Plasma-Instability Suppression,"Physical Review Letters 53,1057-1060(1984).
[2]R.W.Gerchberg,"A practical algorithm for the determination of phase from image and diffraction plane pictures,"Optik 35, 237-250(1972).
[3]H.Aagedal,M.Schmid,T.Beth,S.Teiwes,and F.Wyrowski,"Theory of speckles in diffractive optics and its application to beam shaping,"Journal of Modern Optics 43,1409-1421 (1996).
[4]Y.Lin,T.J.Kessler,and G.N.Lawrence,"Design of continuous surface-relief phase plates by surface-based simulated annealing to achieve control of focal-plane irradiance,"Opt.Lett.21,1703-1705(1996).
[5]S.Wen,J.Hou,C.Yang,H.Yan,Q.Shi,and L.Zhou,"Design and Fabrication of Large-Aperture Continuous Phase Plates for Back Lighting,"Laser & Optoelectronics Progress 48,052201-052201-052201-052205(2011).