αβ?dq?0坐标系下高压电机起动特性的分析
2018-09-12顾海勤杨奕张蔚顾雪政黄媛媛
顾海勤 杨奕 张蔚 顾雪政 黄媛媛
摘 要: 三相感应电动机的起动过程较为复杂,而稳态特性曲线又无法准确描述实际情况,为了准确计算电机的起动特性,在[αβ?dq?0]坐标系下建立电动机的动态数学模型。充分考虑到电动机的实际负载,起动过程中转子参数的变化,分析并计算了电动机的起动特性与起动时间。计算结果表明,动态特性曲线比稳态特性曲线更符合电动机起动的实际情况,为设计满足客户需求的电机提供了准确的参考依据。
关键词: 三相感应电动机; 起动特性; 起动时间; 坐标变换; 数学模型; 动态特性曲线
中图分类号: TN99?34; TM343 文献标识码: A 文章编号: 1004?373X(2018)17?0116?03
Abstract: The starting process of three?phase induction motor is complex, and the steady characteristic curve can′t accurately describe the actual situation. The dynamic mathematical model of three?phase induction motor was established in [αβ?dq?0] coordinate system to calculate the starting characteristic of the motor accurately. By fully considering the actual load of the motor, and change of rotor parameters during starting, the starting characteristic of the motor are analyzed, and its starting time is calculated. The calculation results show that, in comparison with the steady characteristic curve, the dynamic characteristic curve is more suitable for the practical starting characteristic, and the characteristic provides the accurate reference data for the motor satisfying the customer need.
Keywords: three?phase induction motor; starting characteristic; starting time; coordinates transform; mathematical model; dynamic characteristic curve
0 引 言
近些年来,随着造纸、石化、钢铁、水处理等行业生产规模的不断壮大,高压电动机的需求量在不断提高,单机容量也越做越大。电动机采用直接起动法简单方便,成本低廉,但缺点是起动电流过大,一般会达到额定电流的4~7倍,尤其是频繁起动的电动机往往会对电网及其他用电设备的稳定性造成一定的影响。因此研究电动机的起动过程对设计符合实际工况的高性能电机有着极其重要的现实意义。
电动机的起动过程是一个动态环节,虽然采用稳态运行理论研究电机的起动比较简便,但是无法准确描绘电动机的整个起动过程[1?3],所以对于一些控制要求较高的电机需要利用动态分析的方法计算起动过程以提高设计的准确性。本文建立了三相感应电动机在[αβ?dq?0]坐标系下的状态方程,通过求解状态方程得到了电动机的动态特性曲线,再结合实际负载信息从而准确计算出电动机的起动时间。
1 动态数学模型的建立
电动机起动时的转速是不断变化的,其运动方程是一非线性且含有时变系数的微分方程。通常先将电动机的运动方程改写成以电流作为状态变量的状态方程,然后采用数值法进行求解[4]。在[A?B?C]坐标系下建立的状态方程虽然可以直接解出三相绕组的电流,但由于其电感矩阵是一个6×6的矩阵且矩阵中的部分元素又是时变阵,计算较为繁琐。若定子采用[αβ]坐标系,转子采用变换到定子边的[dq]坐标系,则在该坐标系中,电机的电感矩阵和旋转电感矩阵均为常数阵;因此将[A?B?C]坐标系变换到[αβ?dq?0]坐标系可以大大简化状态方程的计算。根据[A?B?C]坐标系与[αβ?dq?0]坐标系之间的转换关系,以及电动机定转子零序电流为零等条件可建立如下的状态方程[5?6]:
2 起动特性与时间的计算
电机起动时,转子电流将比额定值大很多,此时漏磁磁路中的铁磁部分将达到饱和,从而使漏磁磁阻变大、漏抗变小。同时,转子电流频率又随转速的增加而不断减小,从而使得转子各参数也发生相应的改变。考虑以上因素,文献[9?10]对转子各参数进行了修正,即:
式中:[R2],[R2s]和[R2n]分别为任意转速下、起动时和额定运行时转子的相电阻值;[X2],[X2s]和[X2n]分别为任意转速下、起动时和额定运行时转子的漏电抗值;[s]和[sn]分别为任意转差率和额定运行时的转差率。
电动机起动过程中,转子角速度[ωr]的值是不断变化的,因此式(1)就是一非线性微分方程。对于此类方程一般只能采用數值法对其进行求解,在电机工程中常使用四阶龙格?库塔法。求解时设起始时刻为[t0],则有 [isαt0=0],[isβt0=0],[irdt0=0],[irqt0=0]。根据给定的初始值并采用四阶龙格?库塔法对其进行计算,直至电机的电流和电磁转矩达到稳定值为止,即可算出电机的整个动态起动过程。此外根据电机达到稳态时的计算次数[n]以及时间步长[h]可求得电机的起动时间[t=nh]。采用这种算法时,只要时间步长[h]取值足够小,其计算精度完全能满足实际需求。计算表明,对于50 Hz电机,时间步长取0.000 3 s比较合适。
3 计算结果及分析
现以一个1 120 kW,2极,50 Hz电机为例,按上述数学模型及算法对其起动特性进行计算,折算到电机轴上的总转动惯量为29.5 kg·m2。表1为起动过程中的负载信息。图1,图2分别为采用稳态法和动态法计算得到的特性曲线。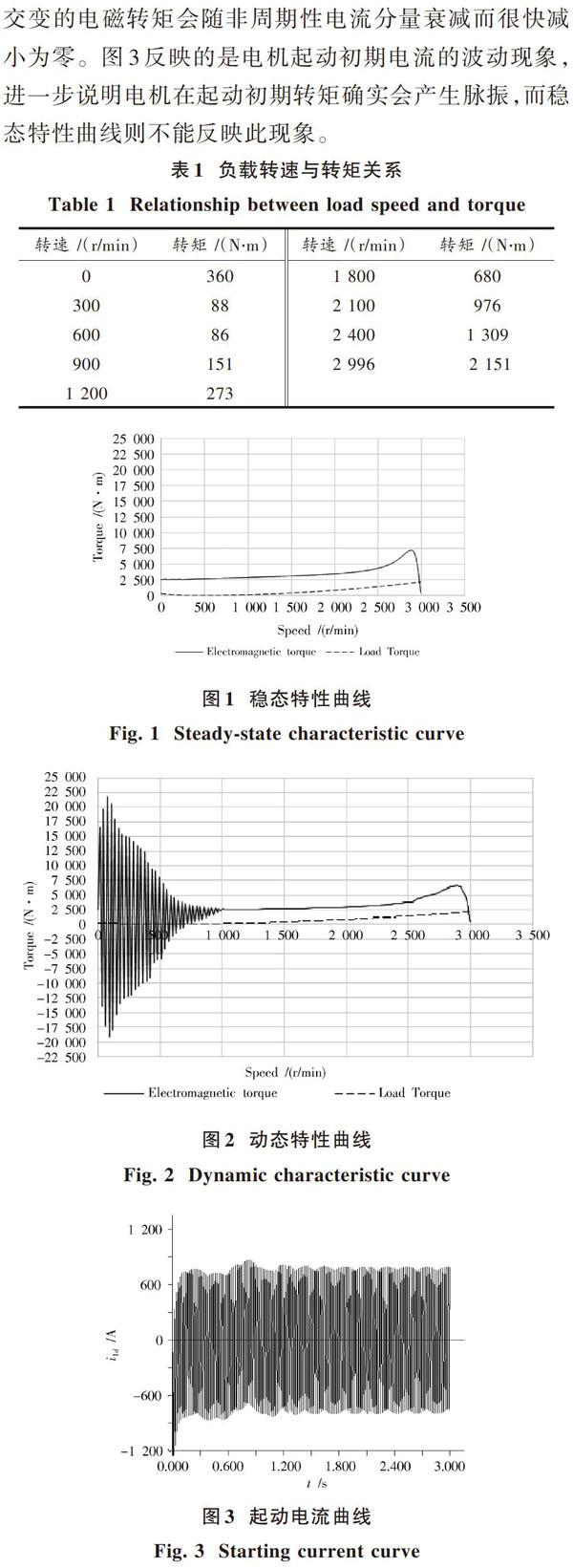
对比图1和图2可以看出,动态特性曲线和稳态特性曲线总的变化趋势是相同的,但在起动初期动态特性曲线中转矩产生了很强的脉振分量。产生脉振的主要原因是电动机起动时定子电流中除含有基频交变分量外,还存在非周期性分量和低频交变分量。后两者与频率为[(1-s)f1]转子电流在空间上产生静止的磁场,此静止磁场与同步旋转磁场相互作用产生交变的电磁转矩。交变的电磁转矩会随非周期性电流分量衰减而很快减小为零。图3反映的是电机起动初期电流的波动现象,进一步说明电机在起动初期转矩确实会产生脉振,而稳态特性曲线则不能反映此现象。
在起动中期,同一转速下,按动态与稳态求得的转矩几乎是相同的。但到了临界转速附近,可以明显观察到,用稳态理论求出的电磁转矩(最大转矩)要大于用动态理论所求得的电磁转矩。一般情况下,电机制造商所提供的最大转矩值是按稳态理论求出的,这就解释了实际测试的最大转矩往往会比电机制造商所提供的值要小这一问题。实际测试可知,电机的实际起动时间也更接近动态理论计算值。以上分析表明,由动态理论求得的动态特性曲线更符合电机起动的实际情况。
4 结 语
为了更精确地分析电动机的起动过程,简化运动方程的计算,本文采用坐标变换,在[αβ?dq?0]坐标系下建立了电动机的动态数学模型,通过计算得到了电机的动态特性曲线和起动时间。分析动态特性曲线并对比稳态特性曲线,解释了以往稳态理论中无法描述的现象,也证明了动态特性曲线更能反映电动机的起动情况,为设计满足客户实际需求的电机提供了重要的理论依据。
参考文献
[1] 赵云,刘世琦,李晓明,等.考虑电磁暂态过程的大功率异步电机全压起动方法[J].高电压技术,2013,39(2):464?473.
ZHAO Yun, LIU Shiqi, LI Xiaoming, et al. Full voltage star?ting method of high?power asynchronous motor considering electromagnetic transient process [J]. High voltage engineering, 2013, 39(2): 464?473.
[2] 乔歆,李建东.三相感应电动机动态过程的仿真[J].防爆电机,2014,49(2):21?23.
QIAO Xin, LI Jiandong. Simulation of dynamic process of three?phase induction motor [J]. Explosion?proof electric machine, 2014, 49(2): 21?23.
[3] 陈振锋,钟彦儒,李洁,等.转子电阻变化对电力牵引感应电机起动转矩的影响[J].电工技术学报,2011,26(6):12?17.
CHEN Zhenfeng, ZHONG Yanru, LI Jie, et al. Influence of rotor resistance variation on starting torque of induction motors in electric traction [J]. Transactions of China electrotechnical society, 2011, 26(6): 12?17.
[4] 汤蕴璆,张奕黄,范瑜.交流电机动态分析[M].北京:机械工业出版社,2004:57?58.
TANG Yunqiu, ZHANG Yihuang, FAN Yu. Dynamic analysis of AC motor [M]. Beijing: China Machine Press, 2004: 57?58.
[5] 蔡卓剑,赵荣祥,汪槱生,等.一种多相异步电机的通用数学模型[J].中国电机工程学报,2015,35(15):3929?3938.
CAI Zhuojian, ZHAO Rongxiang, WANG Yousheng, et al. A general model of multiphase induction machines [J]. Procee?dings of the CSEE, 2015, 35(15): 3929?3938.
[6] 田铭兴,励庆孚,王曙鸿.交流电机坐标变换理论的研究[J].西安交通大学学报,2002,36(6):568?571.
TIAN Mingxing, LI Qingfu, WANG Shuhong. Research of the reference?frame transformation theory of AC machine [J]. Journal of Xian Jiaotong University, 2002, 36(6): 568?571.
[7] 高景德,张麟征,黄立培.异步电机起动过程的研究[J].电工技术杂志,1984(1):1?6.
GAO Jingde, ZHANG Linzheng, HUANG Lipei. Study on the starting process of asynchronous motor [J]. Electric enginee?ring, 1984(1): 1?6.
[8] 靳桂洪.降压起动下异步电机起动参数的研究与分析[J].价值工程,2014,33(22):52?54.
JIN Guihong. Research and analysis of starting parameters of induction motor when reduced?voltage starting [J]. Value engineering, 2014, 33(22): 52?54.
[9] 孙津济,房建成,王建民.异步电动机软起动过程中的振荡[J].电工技术学报,2007,22(2):15?21.
SUN Jinji, FANG Jiancheng, WANG Jianmin. Oscillation in soft?starting of induction motor [J]. Transactions of China electrotechnical society, 2007, 22(2): 15?21.
[10] 耿士广,胡安,马伟明,等.矢量控制感应电机起动机理及直流预励磁研究[J].电工技术学报,2011,26(3):29?35.
GENG Shiguang, HU An, MA Weiming, et al. Vector control start?up mechanism of inductor motor and research of DC pre?excitation [J]. Transactions of China electrotechnical society, 2011, 26(3): 29?35.
