βNodeRank：一种对社交网络节点重要性评估的方法

徐达 杜彦辉 芦天亮 翟瑞

摘 要： 现有基于PageRank算法的社交网络节点重要性评估方法聚焦在社交网络节点出入度、边权值上，忽略了社交网络节点所在网络结构上位置差异的因素。分析现有基于PageRank算法的方法对社交网络节点重要性评估缺陷，提出改进评估方法βNodeRank。通过原理分析和实验分析对改进方法的优势进行比较，结果表明改进方法在社交网络节点重要性评估上更加合理。

关键词： PageRank； βNodeRank； 社交网络； 节点重要性； 社区； 评估

中图分类号： TN711?34； TP20 文献标识码： A 文章编号： 1004?373X（2018）17?0085?05

Abstract： The available PageRank algorithm based node importance evaluation methods for social network mainly focus on the node access degree and edge weight of social network， but ignores the effect of location difference of the social network node on network structure. An improved node importance evaluation method for social network is proposed on the basis of βNodeRank by analyzing the node importance evaluation defects of social network based on the available PageRank algorithm. The advantage of this improved method is analyzed with principle analysis and experiment analysis， and the results show that the method is reasonable for node importance evaluation of social network.

Keywords： PageRank； βNodeRank； social network； node importance； community； evaluation

0 引 言

随着针对社交网络上信息溯源、信息传播机理和信息干预与管控等研究的兴起，对社交网络节点重要性评估成为社交网络研究的重要基础和分支。数据处理能力的提升和社交网络提供大量高价值数据给节点重要性评估方法研究提供了支持，但在社交网络节点重要性评估方法研究中也存在诸多挑战。社交网络上用户是否产生、传递信息受到内因和外因的作用；社交网络用户之间关系复杂，社交网络用户不同程度聚集在一起，除通过如共同标签、共同需求、共同兴趣等社交网络社区划分外，很难找到其他明确划分社交网络用户聚集的界限。这都对评估社交网络中传递信息最快节点、最活跃节点带来了困难，因此对社交网络节点重要性评估需要充分考虑社交网络区别其他复杂网络的特性。

本文分析了一种基于节点度的评估方法[1]，针对原方法从社交网络节点连接情况出发而忽略节点所处社交网络结构位置影响的不足，提出一种结合节点度和社区因素的改进评估方法，从理论分析和真实数据测量研究社交网络节点重要性评估。不同于已有方法[2?3]对节点度的具体分析或降低算法复杂度，改进方法结合社交网络社区因素，能够更合理完成社交网络节点重要性评估。

1 相关工作

社交网络是一种典型的复杂网络，具有“小世界”“度分布”“聚集”等特征[4]。对复杂网络节点重要性排序研究，许多研究者选择从复杂网络节点的某种或多种统计特征的角度来分析节点重要性。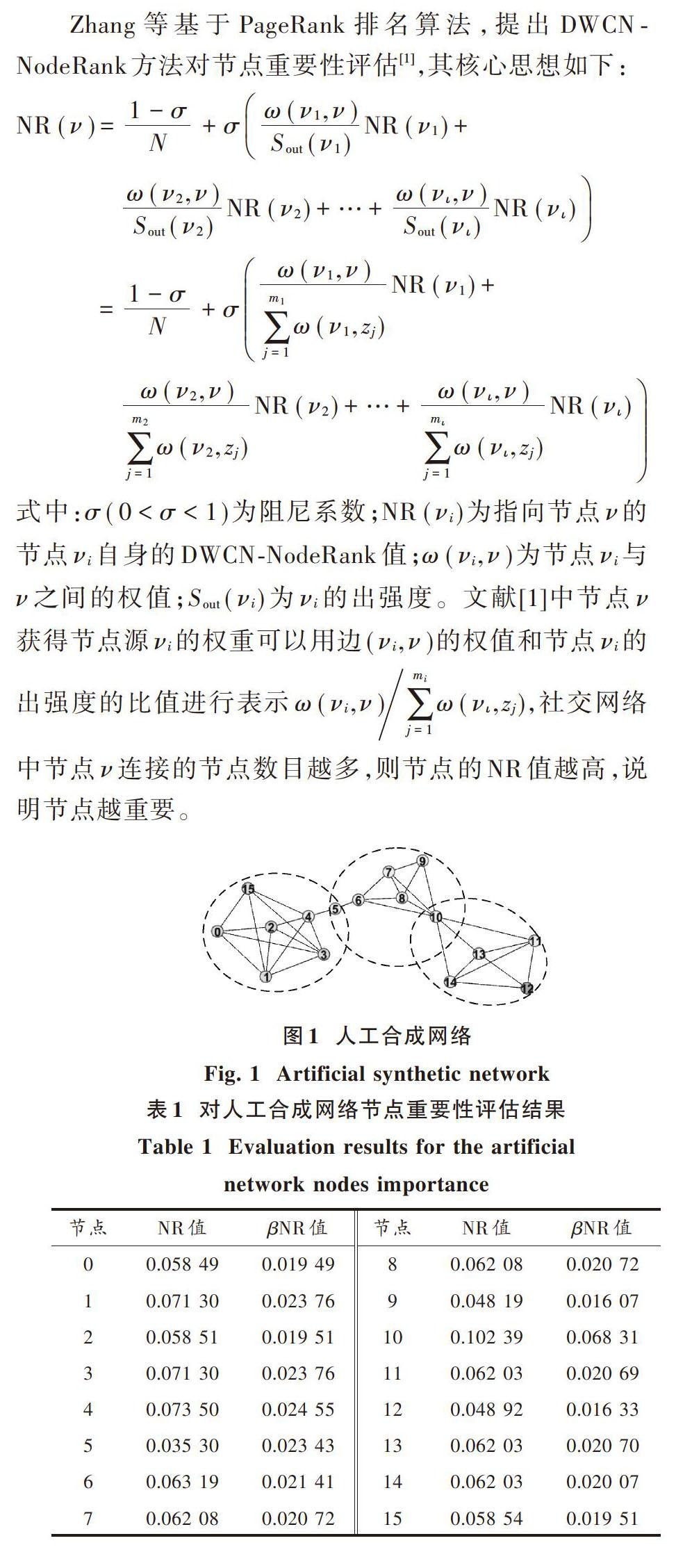

文献[1]基于PageRank排名算法，提出DWCN?NodeRank方法对节点重要性评估，完成对加权有向社交网络节点重要性排序。文献[3]考虑节点间边的权值，认为节点重要性与节点的入度、出度和总度相关，提出改进PageRank排名算法对复杂网络节点重要性排序的方法。文献[5]提出一种改进基于凝聚度的节点重要性评估方法，引入节点连接边的重要度评估，综合考虑节点的连接特性对节点重要度的影响。通过节点的连接情况对网络中节点重要性评估是常见的研究方法，但忽略了节点所处网络结构位置对节点重要性的影响。

文献[6]基于社交网络真实数据分析得出结论，集聚度高节点相对集聚度低节点在复杂网络上扩散信息更快。Kitsak等提出节点重要性与节点所处复杂网络的位置相关[7]，并利用k核分解，通过递归将整个网络划分成层次，得出节点重要性排序指标；首次通过理论和实验验证，节点重要性与节点所处复杂网络的位置是相关的。研究从网络结构特性出發，但指标有一定的局限性。

在社交网络节点重要性评估中，节点入度、出度和总度是重要的指标，节点所处网络结构位置也对节点重要性评估具有重要影响。本文从社交网络节点度出发，同时考虑节点社区连接情况对社交网络节点重要性评估。

2 基于NodeRank节点重要性评估

图1中网络共有16个节点、33条边、3个社区（虚线圈表示社交网络社区），其中节点5和节点10分别从属两个社区。由上述结果可知节点5在整个网络中NR值最小，则认为节点5为整个网络中最不重要的节点。分析图1网络可知，节点5作为“骑墙节点”在网络中连接节点4和节点6、社区1和社区2，在图1所示网络中的重要性不言而喻。由DWCN?NodeRank[1]得出的结论与文献[7?9]中方法得出的结论都有较大出入，分析DWCN?NodeRank在图1网络中节点重要性排序过程，发现DWCN?NodeRank聚焦于节点的出入强度、有向边的权值，而忽略了复杂网络中多社区与重叠社区对社交网络节点重要性排序的影响。

3 基于βNodeRank节点重要性评估方法

PageRank算法是为互联网页面排名而设计，社交网络与互联网虽然都是复杂网络，但两者存在明显的区别，直接基于PageRank算法对社交网络节点重要性评估是不合理的。在社交网络中通常由性质相似的节点组成社交网络社区，社区结构是对社交网络节点聚集特性的刻画[10]。社交网络中，节点从属一个或多个社区，当节点从属的社区越多，则表明节点越趋近社交网络结构中心，在社交网络结构中越重要。对社交网络节点重要性评估需要将节点按现实情况划分至各社区，考虑节点在社区间连通的贡献，提高社交网络节点重要性评估的准确性。因此社交网络节点的重要性评估需要考虑节点出入度、边权值和节点社区等因素。Zhang等基于PageRank排名算法，提出DWCN?NodeRank方法对节点重要性排序[1]，忽略节点对社区连通贡献，不能满足对社交网络节点重要性评估，需要进行改进。针对上述問题，本文在分析和总结现有方法基础上，提出基于[βNodeRank]方法对社交网络节点重要性评估的方法。

首先，大量的实验数据结论[7?9]表明社交网络中某些节点度数较低，但处于整个网络中的关键位置。其次，社交网络中个体之间的相似性、个体之间的某种联系和个体的兴趣爱好等让个体在社交网络中呈现聚集状态形成各类网络社区，在社区内信息传播、扩散的速度更快，社区是社交网络节点重要性评估不可忽视的因素。综上所述，提出改进方法[βNodeRank]，设置调节参数[βι]对社交网络节点重要性评估引入社区因素：

式中，[βι=tN]，[t]为节点从属社区数，[N]为社交网络节点总数。对图1所示重叠社区社交网络基于[βNodeRank]节点重要性评估的结果如表1所示。在图1所示网络重要节点重要性评估过程中，相比NodeRank方法所得结论，[βNodeRank]方法所得结论节点15和节点14的重要性排名略微有所下降，节点5的重要性排名大幅度提升；分析图示网络结构，节点15和节点14都具有节点度数高、从属社区单一，节点5具有节点度数低、从属社区多的特点。在[βNodeRank]引入调节参数[β]，能够提高节点度数低但从属社区多节点的NR值，降低节点度数高但从属社区单一节点的NR值。由此可见， [βNodeRank]对图1所示网络中节点重要性评估更加合理，所得结果与文献[7?9]中方法得出结论也更接近。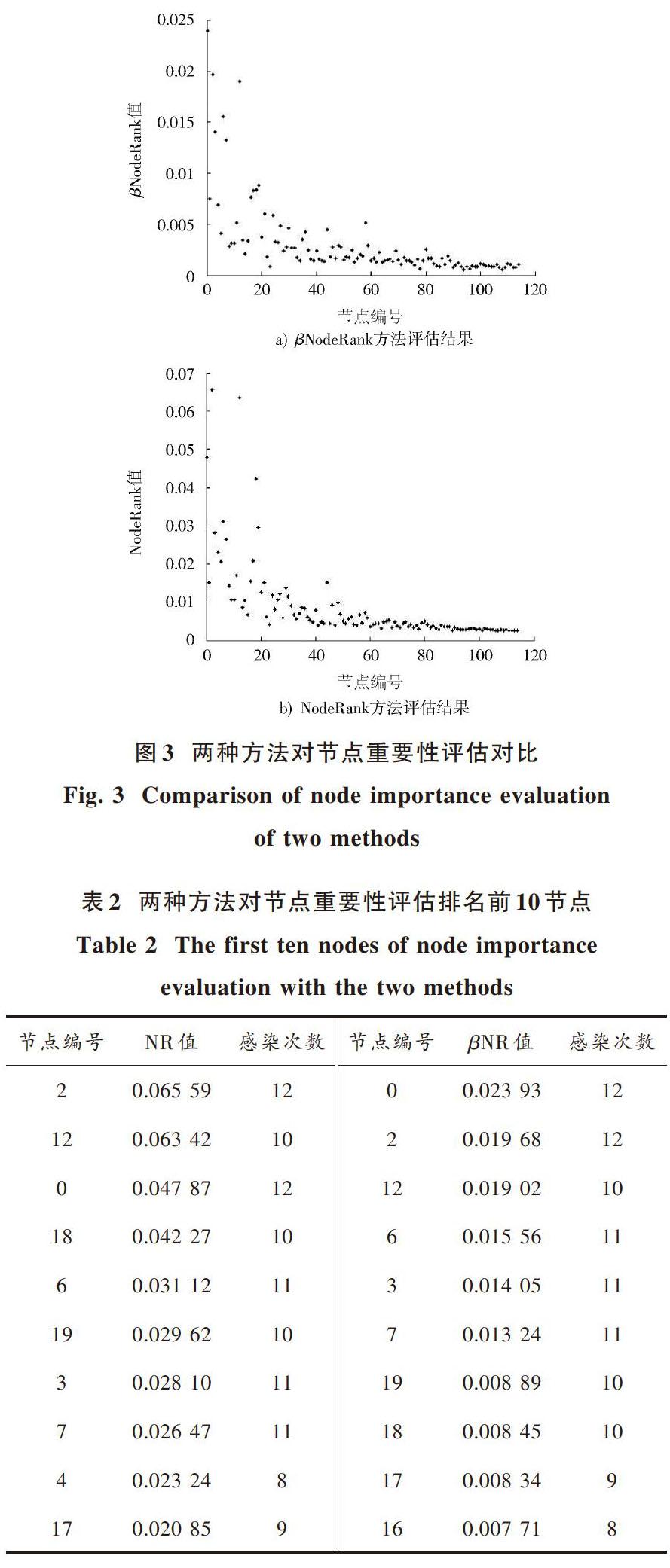

COPRA算法在标签传播过程中采用同步更新的策略，节点[t]次迭代基于[t-1]次迭代邻居标签列数据对，主要的步骤如下：

1） 对社交网上所有节点进行初始化，每个节点引入唯一标签列，标签列中的数据对根据社交网中节点的连接状况进行添加。

2） 设定从属系数阈值[1v]，[v]是节点的最大社区从属数。一个节点标签中所有数据对都小于设定阈值，保留最大的从属系数的数据对，将其他数据删除，如果超过一对的最大从属系数对，将其中进行随机选择。在节点标签列数据被删除后，将对其从属系数更新，保持从属系数和为1。

3） 经过若干次迭代后，当[t]次迭代结果和[t-1]次结果相同，则停止迭代。

4） 根据结果具有相同标签的节点将被划分至同一社区。

实验结果证明COPRA算法虽然迭代过程具有随机性[11]，但能够对有向加权网络进行准确的社区划分。图2为人工合成网络基于COPRA算法[11]进行社区划分。网络初始化后，设定阈值为[v=3]，如图2a）所示节点15标签列数据对为{（0，[14]），（1，[14]），（3，[14]），（4，[14]）}，在迭代前对节点15标签列数据对更新为（1，1），经过数次运算，得到重叠社区划分结果如图2b）所示，人工合成网络共有社区数3个，节点5和节点10分别从属2个不同社区。

引入病毒模型模拟消息在社交网络中的扩散能为社交网络节点重要性评估方法比较提供支撑。本文引入Wang等提出的传染病模型[12]，模拟社交网络上信息扩散。在2011年文献[13]研究成果中已经证明信息量越大的节点重要性越强。本文利用该成果，定义社交网络中被感染次数越多的节点重要性越强。

4 实验仿真

为验证改进方法[βNodeRank]的可行性和准确性，基于真实社交网络数据进行实验。实验环境为Intel[?] CoreTM i5?4570 CPU@ 3.20 GHz，4 GB内存，Window 7旗舰版SP1操作系统，Gephi?0.9.1，Matlab R2010b编程环境。

社交网络数据采用Newman实验室采集美国大学生橄榄球联赛社会网（Football），并引入病毒模型[12]模拟信息的扩散。本文对社交网络进行病毒感染，分别选择不同的节点为初始感染点，设定[α] =0.85（[α]为未感染节点直接与感染节点连接被感染率），[ζi，t]=0.15（[ζi，t]为节点[i]在时刻[t]的免疫率），[δ]=0.5（[δ]为感染病毒节点自身痊愈率），对社交网络进行感染，当感染节点占所有节点数的85%时，停止病毒传播，实验20次后，取各节点被感染次数的众数为最终结果。实验网络共包括节点115个、边613条、整个网络平均度为10.66、平均加权度为5.33。对Football网络节点进行编号后，基于COPRA算法对Football社交网络进行社交网络社区发现，得知该网络共有社区10个，随之确定各节点从属社区，并标记各节点[βι]值，基于[βNodeRank]方法对节点重要性排序。

基于[βNodeRank]方法对Football网络节点重要性评估，经运算得出如图3a）所示结果与基于DWCN?NodeRank方法得出图3b）所示结果进行对比分析。在两种方法中阻尼系数均设置为0.85，结果值准确度为[10-5]，横坐标为Football网络各节点编号，纵坐标为结果值。

对比分析两种方法所得结果，在节点编号相同的情况下，两者结果数据值差异较大，但大体上两者结果分布形态相对接近，少许节点有出入。本文选取部分代表性节点进行分析，两种方法得出网络节点重要性评估结果中排名前10的节点分别如表2所示。

将社区节点分为10簇代表网络中社区情况，图4表示节点在Football网络中连接情况。其中图4a）为所有节点相互之间的连接情况。由表2数据对比分析，排名前3的节点0、节点2和节点12在网络中连接情况分别如图4b），图4c）和图4d）所示。相对节点2和节点12度数高但只连接3个社区，节点0度数高并且连接5个社区在社交网络上更加重要。值得说明的是节点12被感染的次数为10次，连接社区为3个，但是节点12所连接的节点大部分是高分值节点，所以节点12在两种节点重要性评估方法中都具有较高评分值。对比分析两种方法的结果，[βNodeRank]在社交网络上重要节点排序过程中能调整度数相对较低，但连接社区多节点的重要性强度。依据节点重要性重新排序，所得结果也与病毒感染模型[12]结论吻合。

基于真实网络数据的分析得出，改进方法更合理、准确地对社交网络节点重要性评估，评估方法所得结论符合PageRank算法“从高评分页面链接得到的页面也是高评分页面”的回归思想，并且能够提高重要节点分值，降低非重要节点分值。

5 结 语

本文分析了基于PageRank算法对社交网络节点重要性评估方法中忽略社区作用的缺陷，在此基础上针对原算法不足，提出改进的社交网络节点重要性评估方法。结果表明，改进的评估方法[βNodeRank]加入社区因素后，对社交网络节点重要性进行评估，所得评估结果更加合理。社交网络节点重要性评估高度复杂，因此本方法仍然存在不足之处，未来，可进一步的考虑社交网络多因素影响。本方法的提出有助于进一步的分析和探讨。

参考文献

[1] ZHANG K， LI P， ZHU B， et al. Evaluation method for node importance in directed?weighted complex networks based on PageRank [J]. Journal of Nanjing University of Aeronautics & Astronautics， 2013， 45（3）： 429?434.

[2] 杨宏伟，张勇，王焕坤，等.基于负载流的点加权复杂网络节点重要性评估方法研究[J].计算机应用研究，2013，30（1）：134?137.

YANG Hongwei， ZHANG Yong， WANG Huankun， et al. New measure of node importance based on load flow in node?weighted complex networks [J]. Computer application research， 2013， 30（1）： 134?137.

[3] LI G L， LI H， WANG Y R， et al. The solution to node importance in complex networks based on PageRank algorithm [J]. Applied mechanics & materials， 2014， 599： 1777?1780.

[4] 刘建国，任卓明，郭强，等.复杂网络中节点重要性排序的研究进展[J].物理学报，2013，62（17）：9?18.

LIU Jianguo， REN Zhuoming， GUO Qiang， et al. Node importance ranking of complex networks [J]. Acta physica Sinica， 2013， 62（17）： 9?18.

[5] 王甲生，吴晓平，廖巍，等.改进的加权复杂网络节点重要度评估方法[J].计算机工程，2012，38（10）：74?76.

WANG Jiasheng， WU Xiaoping， LIAO Wei， et al. Improved method of node importance evaluation in weighted complex networks [J]. Computer engineering， 2012， 38（10）： 74?76.

[6] CENTOLA D. The spread of behavior in an online social network experiment [J]. Science， 2010， 329（5996）： 1194?1197.

[7] KITSAK M， GALLOS L K， HAVLIN S， et al. Identification of influential spreaders in complex networks [J]. Nature physics， 2010， 6（11）： 888?893.

[8] JIAN Z， PAN J， ZHOU Y. Node importance evaluation based on network heterogeneity [C]// 2010 IEEE International Confe?rence on Communications and Mobile Computing. Piscataway： IEEE， 2010： 188?194.

[9] 李拓晨，侯磊，李永立.一种基于网络整体影响力的节点重要性评估方法[J].情报学报， 2015，34（11）：1143?1151.

LI Tuochen， HOU Lei， LI Yongli. Evaluation method for node importance based on the whole network prestige [J]. Journal of the China society for scientific and technical information， 2015， 34（11）： 1143?1151.

[10] BALAKRISHNAN H， DEO N. Discovering communities in complex networks [C]// 2006 Southeast Regional Conference. Melbourne： [s.n.]， 2006： 280?285.

[11] GREGORY S. Finding overlapping communities in networks by label propagation [J]. New journal of physics， 2009， 12（10）： 2011?2024.

[12] WANG Y， CHAKRABARTI D， WANG C， et al. Epidemic spreading in real networks： an eigenvalue viewpoint [C]// 2003 IEEE International Symposium on Reliable Distributed Systems. Piscataway： IEEE， 2003： 25?34.

[13] 张翼，刘玉华，许凯华，等.一种基于互信息的复杂网络节点重要性评估方法[J].计算机科学，2011，38（6）：88?89.

ZHANG Yi， LIU Yuhua， XU Kaihua， et al. Evaluation method for node importance based on mutual information in complex networks [J]. Computer science， 2011， 38（6）： 88?89.