多晶面银纳米线拉伸形变的分子动力学模拟

孙寅璐，刘丽娜，文 畅，赵健伟

(1.辽宁大学 化学院，沈阳 110036； 2.嘉兴学院 材料与纺织工程学院，嘉兴 314001)

金属纳米线因其独特的机械性质、光电性质、热学性质和磁性质等，被广泛应用于电极材料、光学材料和催化材料等领域[1-5].这些优异的性能与纳米线中的表面结构密切相关，尤其当纳米线尺度小于10nm时，纳米线表面和界面应力将成为控制纳米线形变的主导因素[6-7].为了构建高强度纳米线，研究表面形貌对金属纳米线的形变影响显得十分必要.

理论上通常借助分子动力学模拟来研究不同表面形貌对纳米线强度的影响机制.大量的模拟研究表明，表面形貌能控制金属纳米线的力学性质和形变行为.Yang等[8]实施11种不同的晶面指数侧面的Ag纳米线拉伸模拟时，发现侧面为(10 0 0)和(10 10 0)时纳米线的机械性能增强；而侧面为(10 4 0)和(10 7 0)时纳米线机械性能削弱.Ji和Park[9]在模拟<100>和<110>晶向Cu纳米线的拉伸时发现，拥有正方形截面的纳米线比非正方形截面的纳米线在拉伸过程中拥有更大的应力值.McDowell等[10]在研究侧面为{100}、{110}和{111}晶面的纳米线时，发现纳米线的几何形状和表面特征在一定程度上能影响纳米线的弹性模量.Hasmy等[11]研究了Au纳米线的表面效应，结果表明尺寸较小时重构的表层原子会影响纳米线的失效行为.此外，Deng等[12]发现{111}表面的多晶面孪晶纳米线比普通的孪晶纳米线具有更高的屈服应力和屈服应变.Sun等[13]也证实了多晶面孪晶纳米线是一种有效的孪晶界-表面硬化材料，其高强度是以牺牲其延展性来实现的.Gao等[14]设计了内部含有孔洞缺陷的多晶面单晶Ag纳米线，通过与普通方形纳米线对比发现，多晶面纳米线的机械强度容易受到孔洞缺陷的影响.Zhang等[15]发现表面形貌可决定孪晶界的引入对纳米线起到强化作用还是弱化作用.其研究表明，当纳米线为圆柱形时孪晶界表现为弱化作用；而当纳米线截面为方形时孪晶界表现为强化作用.

实验上通常采用扫描电子显微镜(Scanning Electron Microscope, SEM)、高分辨率透射电镜(High Resolution Transmission Electron Microscopy, HRTEM)等技术来观察纳米线的微观结构.比如SEM可给出材料最终失效后断口的形貌.Rodrigues等[16]观察到了稳态拉伸的铂(Pt)纳米线断裂后的针尖结构，提出了针尖是由(111)和(100)面构成的模型.而利用HRTEM可得到金属纳米线的在拉伸过程中的动态信息.Zheng等[17]将原位拉伸测试技术和HRTEM的联用实施了[001]晶向FCC Au纳米线的拉伸测试，并揭示了其特有的塑性形变和断裂行为.在拉伸过程中纳米线的{111}面在两两交汇处形成台阶，表现出多晶面的结构特征.事实上，在FCC结构纳米晶体在制造过程中多有{111}表面产生.比如采用电化学生长方法制备金属纳米线时，模板内部的凹凸结构会造成纳米线表面的台阶产生[18].

迄今为止，研究者们对不同表面形貌特征的纳米线其弹性形变和初始塑性形变已展开了大量的模拟和实验研究，但是关于表面形貌对金属纳米线的形变影响仍需进一步阐明.众所周知，对于FCC结构金属纳米线来说{111}面是能量最低的密排面，该指数面上难以形成位错，因此表现出对纳米线的强化作用.可是当纳米线结构发生变化时，{111}表面将如何影响纳米线的强度仍不清晰.另外在Rodrigues等[16]和Zheng等[17]的拉伸测试报道中，作者指出多晶面纳米线为脆性断裂，其断裂截面为{100}面，周围侧面为{111}面.而大部分模拟报道的多晶面纳米线的拉伸断裂面均为韧性断裂，各个断裂面均为{111}面[8,13].实验和模拟在断裂面处的差异可能与加载模式、拉伸速率或者初始构型有关[17].关于多晶面对纳米线的力学性质和断裂行为等认识还不完整，有必要对多晶面纳米线的形变机理开展系统研究.

为此，本文以四棱台结构为基本单元，构建了多晶面单晶Ag纳米线模型.采用分子动力学方法实施了不同多晶面结构的纳米线拉伸模拟，以揭示其内在形变机理和断裂行为，为构建高强度纳米线奠定理论基础.

1 模拟方法

构建了FCC构型轴向为[100]晶向的Ag多晶面纳米线，纳米线由多个大小相同且侧面均为{111}面的四棱台组成，如图1所示，左图为多晶面纳米线模型，右图为四棱台结构单元模型.

图2为NW12的初始结构图，其四棱台结构包含8个原子层，通过移动上下两端的固定层实现对纳米线的双向拉伸.FCC原子代表了完美的面心立方结构，用深色表示；其他原子代表低配位原子(包括表面原子)，用浅色表示.

图1 多晶面Ag纳米线模型结构图Fig.1 Structural model of faceted Ag nanowire(a) <100>晶向多晶面银纳米线；(b) 组成多晶面纳米线的四棱台基本结构单元.

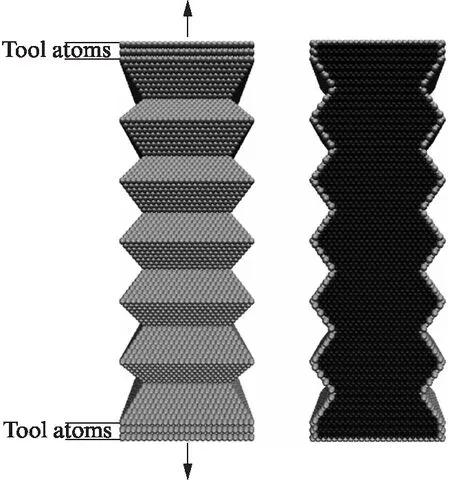
图2 多晶面纳米线NW12的初始构型示意图Fig.2 Schematic of initial configuration of faceted NW12深色原子代表FCC构型，浅色原子代表表面原子.

表1为统计的各纳米线的晶体学特征.AB为四棱台长边，A′B′为四棱台短边，H为四棱台的高度，N为多晶面纳米线包含的四棱台数量，L为纳米线的长度，D为等效直径，其大小等于普通方形纳米线的截面边长.各参数间关系为：

L=H×N+1,

(1)

|AB|=|A′B′|+H,

(2)

(3)

纳米线的长度均为20nm，边长或等效直径均为6nm.由以上公式可知，当等效直径D确定时，可通过改变四棱台高度获得一系列包含不同四棱台数量的多晶面纳米线.以所包含的四棱台数量命名分别为NW4、NW6、NW8、NW12、NW16、NW24、NW32、NW48.体系原子总数在4万到4.7万.

表1 包含不同四棱台数量的银纳米线的晶体学特点

为了揭示多晶面特征表面对纳米线形变的影响，本文还设计了同尺寸的普通方形纳米线作为参考纳米线(NW0).参考纳米线晶向为[100]，其侧面均为{100}面.

采用Johnson解析的分析型EAM势[19]描述Ag-Ag原子间的相互作用，Verlet leapfrog数值积分法[20]获得原子的速度和运动轨迹.体系为正则系综(NVT)，采用校正因子法控制体系温度为一固定值[21].为了模拟真实体系，计算中x、y、z方向均采用自由边界条件.时间步长为2.6×10-15s.体系首先在设定温度下自由弛豫2万步，待达到平衡后，沿[100]晶向(z轴)以每皮秒纳米线总长度的0.025%的应变速率匀速双向拉伸直至断裂.本文的模拟计算均在自主开发的大规模分子动力学仿真平台NanoMD软件[22-23]的支持下完成，该软件的可靠性已经从大量的模拟研究中得到验证[24-31].

2 结果与讨论

图3为多晶面纳米线和NW0纳米线在2K下的应力应变曲线.

图3 在2K下各纳米线的应力应变曲线Fig.3 Stress-strain curves at 2 K(a) 棕黄色曲线为NW24，橘黄色曲线为NW0；(b) 黑色曲线为NW6, 红色曲线为NW8, 蓝色曲线为NW12，绿色曲线为NW16

图4 多晶面银纳米线的屈服应力和AB/A′B′的变化关系Fig.4 Evolution of yield stress as a function of AB/A′B′ in faceted Ag NWs

图3(a)中NW24和NW0的杨氏模量基本相同，但NW24的弹性形变范围明显扩大，其屈服应力增加了1.0GPa，且屈服应变增加了0.02，说明{111}表面能提高纳米线的屈服行为.NW24断裂应变比NW0小，说明{111}表面实现纳米线的强化作用可能是通过牺牲塑性来实现的.文献在报道多晶面孪晶纳米线时也出现类似的情况，其研究表明多晶面孪晶纳米线比普通方形孪晶纳米线的屈服应力增强1.3GPa，屈服应变增加了0.022，断裂应变减小0.08[13].图3(b)中，随四棱台数量增加杨氏模量得到强化[10]，且弹性形变范围明显扩大.一般来说，引入表面形貌或是孪晶界等结构会对纳米线的屈服应力有显著影响，而使杨氏模量改变的报道并不多见[8,12-13].另外，与NW24的韧性断裂不同，4种多晶面纳米线均表现为塑性流动受限的脆性断裂.

将各多晶面纳米线的屈服应力和四棱台长边与短边比值作图，如图4所示.随比值增加，长边与短边差值增大，四棱台高度增加、数量减小，屈服应力呈现为先增加后减小的趋势.比值刚大于1时，方形纳米线开始向多晶面纳米线过度，多晶面表现为对纳米线的强化作用，直至比值为1.185时达到最大屈服应力.随着短边不断减小，短边对纳米线的削弱作用逐渐增加，使得多晶面的强化作用不断下降，直至比值约为1.4时强化作用消失.随着比值继续增大，纳米线的短边越来越小，削弱作用愈发明显，屈服应力迅速下降.总体来看，{111}表面并不总是表现为对纳米线的强化作用，当比值大于1.4左右时引入{111}表面将会弱化纳米线.

2.1 多晶面纳米线强化作用的微观形变分析

以NW24为例揭示{111}表面对纳米线的强化作用机制.根据中心对称参数法，统计结构中不同类型的原子数量分析两种纳米线在拉伸过程中的结构演变.各类原子在形变过程中此消彼长，但原子总数保持不变.当处于弹性拉伸阶段时，纳米线内部结构保持不变.当拉伸到达屈服点时，塑性形变开始发生，并随外力载荷不断加剧，总体表现为FCC原子数下降，其他原子或HCP原子数增加[32].

在图5(a)为NW0在拉伸过程中不同类型原子的比例变化.在弹性区域，纳米线内部只有FCC和表面原子，比例分别为86.7%和13.3%.在屈服点以后，大量FCC向HCP原子转化，HCP原子迅速增加，当应变为0.77时原子比例可达15%.随拉伸不断进行，HCP原子缓慢增长直至纳米线断裂.表面原子增幅仅为2%，其影响可以忽略不计.

图5 (a) NW0和(b) NW24 3种类型原子比例与拉伸应变关系Fig.5 NW0(a) and NW24 (b) fractions of three categories of atoms with tensile

图5(b)为NW24在拉伸过程中不同类型原子的比例变化.由于特殊的表面特征，纳米线初始结构中就包含了HCP原子(台阶交界处).表面原子、FCC原子和HCP原子的比例分别为16.1%、81.9%和2.0%.在屈服点以后，大量FCC原子向HCP原子转化，HCP原子迅速增加.当到达第一最小应力时，HCP原子比例可达8%.与NW0不同，在FCC原子比例出现多处平台，尤其是应变在0.1和0.13之间以及0.138和0.155之间，FCC原子比例始终保持在80%左右，之后FCC原子开始呈阶梯下降.多晶面纳米线的塑性形变为位错成核、增殖和消失的竞争模式，导致了平台的出现.在单晶Al纳米线的拉伸试验中也观察到类似现象，作者指出流变应力是位错的成核速率和消失速率共同作用的结果[33].{111}面使得纳米线表面能量较低，结构稳定，易于重结晶，因而实现纳米线的强化作用.

2.2 多晶面纳米线的断裂模式研究

考察了在每皮秒纳米线总长度的0.025%的拉伸应变速率下NW6、NW8、NW12和NW16四种多晶面Ag纳米线在2、50、100、150、300和400K下的屈服行为，如图6所示.

图6 4种多晶面Ag纳米线在不同温度下的应力应变曲线Fig.6 Stress-strain curves for faceted Ag NWs at different temperatures(a) 2, (b) 50, (c) 100, (d) 150, (e) 300和(f) 400K黑色曲线为NW6,红色曲线为NW8,蓝色曲线为NW12，绿色曲线为NW16

总体来看，各纳米线的屈服应力随温度升高而降低.此外，各纳米线在不同温度下的塑性形变也表现出很大差异.在2K下均表现出脆性断裂(图6(a))，在50K(图6(b))和100K(图6(c))下开始有部分纳米线向韧性断裂转变，而当温度升高至150K以上时各纳米线均表现为韧性断裂(图6(d)～(f)).

除温度外还考察了应变速率对四种纳米线的强度影响，应变速率范围从每皮秒纳米线总长度的0.025%增加到0.1%，分别在2K和300K下实施拉伸，如图7所示.

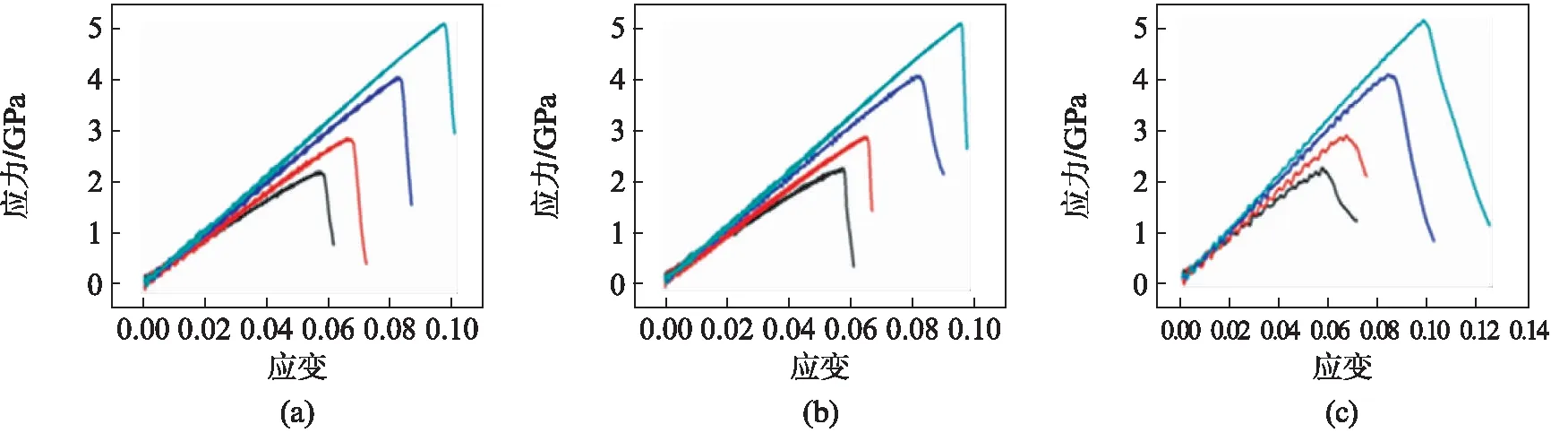
图7 4种多晶面Ag纳米线在不同应变速率下的应力应变曲线Fig.7 Stress-strain curves for faceted Ag NWs with different strain2K下： (a) 0.025%, (b) 0.05%和(c) 0.1%; 300 K下： (d) 0.025%, (e) 0.05%和(f) 0.1%黑色曲线为NW6,红色曲线为NW8,蓝色曲线为NW12，绿色曲线为NW16

在2K下，应变速率的改变基本上不会影响纳米线的屈服行为，此时的纳米线处于准静态拉伸(图7(a)～(c))[25, 29, 34].随温度升高，较大的应变速率开始表现出对纳米线的强化作用，并且随温度升高这种强化作用愈发明显(图7(d)～(f))，此时的纳米线处于非平衡态拉伸[35].

随温度升高，相同的拉伸冲击使纳米线由准平衡态拉伸向非平衡态拉伸转变.在准平衡态拉伸时，原子动能分布的涨落幅度小，纳米线的强度对拉伸速率的依赖关系不明显.而在非平衡态拉伸时，随拉伸速率增加，涨落幅度增加，能量富集区域造成原子运动异常剧烈而形成位错，原子的形变以无定形结构为主，其晶粒内部的位错活动会受到结构稳定的{111}表面阻挡，因而表现出较大的应变速率对纳米线的增强作用.

从断裂模式来看，2K下应变速率的变化不会改变纳米线的脆性断裂.而在300K下，即使采用较低的应变速率也没有脆性断裂发生，均表现为韧性断裂.由此可知，相比于应变速率，温度更能影响多晶面单晶纳米线的断裂模式.

图8 在2K和300K下NW16的应力应变曲线Fig.8 Stress-strain curves of NW16 at 2K and 300K(b)是(a)中1a～1g部分的放大图.

为了揭示两种断裂行为的差异，我们分别对2K和300K下NW16拉伸形变位图进行了分析，图8阐述了NW16在2K和300K下的应力应变关系，应力应变曲线上标记的点1a～j和2a～c分别对应于图9(见第496页)和图10(见第496页)的形变位图.为了视图效果更佳明晰，图9和10中只显示了表面框架原子和位错原子.

如图9所示，在到达弹性极限后，第1位错(先导位错)从表面台阶处成核(图(a))，沿{111}面滑移、增殖并产生层错(图(b)和图(c)).已有文献证实当样品尺寸减小至纳米数量级时，Frank-Read位错源不再被激活，纳米线的表面将成为塑性形变的控制因素[36-37].然而，第1滑移面在到达表面时并没有反射到另一滑移方向，而是趋向于部分消失或是完全消失(图(d)和图(e))，这表明{111}面具有良好的吸纳位错的能力.但这并不意味着体系仍保持完美结构，事实上纳米线在其位错出现过的地方已经发生破裂(图(e)～图(f)中的斜线).随应变不断加大，不同的滑移系交错开动形成十字交叉(图(g)).而这些十字缺陷随后又逐步演变成位错团簇(图(h)和图(i)).位错团簇的出现和增加导致了纳米线的颈缩和断裂(图(j)).总体来看，300K下多晶面纳米线的塑性形变机理以不全位错的滑移和增殖为主导，各断裂面均为{111}面.

在2K下多晶面纳米线的塑性形变与300K的情况显著不同.如图10所示，塑性形变与位错滑移无关.屈服点之后，在四棱台短边交界处随即萌生开口，此开口的形成和扩张导致了纳米线的迅速断裂.断裂截面为{100}面，周围侧面为{111}面.与Zheng等在Au纳米线的拉伸测试中观察到的断裂行为一致[17].

图9 300K下NW16的拉伸位图(图8中1a～1j)Fig.9 Snapshots of NW16 under tension at 300 K correspond to 1a—1j in Fig.8

图10 2K下NW16的拉伸形变位图(图8中2a～2c)Fig.10 Snapshots of NW16 under tension correspond to 2a—2c in Fig.8(a) 屈服点处;(b) 屈服点后5ps; (c) 屈服点后10ps.

本文以低能量的四棱台结构为基本单元，构建了<100>晶向多晶面单晶Ag纳米线，利用分子动力学方法模拟了纳米线在拉伸载荷下的形变行为，详细考察了单元结构、体系温度、拉伸速率等因素对纳米线的力学影响，揭示其内在的弹性形变和塑性形变机理.结果表明，当四棱台长边与短边比值小于1.4时，{111}表面的强化作用占主导地位，而当比值大于1.4时多晶面对纳米线起到弱化作用.从断裂模式看，随四棱台数量减少，多晶面纳米线将由韧性断裂向脆性断裂转变，且温度相比于应变速率更易影响多晶面纳米线的断裂行为.本文所提出的多晶面纳米线的强度作用规律以及不同断裂模式的机理研究，对设计和构建高强度、低塑性纳米器件提供一些指导和借鉴.