大型预应力反力墙的有限元分析和实用性研究
2018-09-12张晋元王永伟
张晋元 王永伟 王 昊
(天津大学建筑工程学院,天津 300350)
0 引 言
反力墙系统由反力墙和试验台座组成,属于特种结构。大型反力墙通常采用“L”型平面,通过固定于墙体上的水平液压加载装置为试件提供单/双向水平加载力,模拟结构或构件受水平地震作用并研究其抗震性能。为了保证试验结果的准确性,反力墙在使用过程中需承担较大的反力并且必须严格控制位移和变形,所以其既要有足够的强度,也要有足够的刚度。反力墙采用箱型结构体,可以很好的满足刚度要求。同时,在隔墙上开门洞,连通每个隔间,便于安装加载装置。裂缝是影响混凝土结构强度和耐久性的主要原因,采用预应力混凝土结构,可以通过在墙体内布置竖向无粘结预应力筋来抵抗墙体所承受的拉力,防止裂缝的产生[2]。本文采用Midas/Gen软件对某预应力反力墙系统进行有限元分析,确定不同工况下的受力和变形,为反力墙的使用提供依据。
1 工程概况
本工程是某高校新建的反力墙系统。反力墙A和反力墙B采用箱型结构体,相互垂直,拐角不相连。反力墙A长19.1 m,高17.1 m,总厚5.2 m,其中,单片墙肢厚度为0.7 m。反力墙A正面以隔墙为分界线,分为六个加载区,每个加载区均匀布置间距为0.5 m×0.5 m的加载孔,不同加载区的相邻加载孔横向相距1 m。反力墙B长14.9 m,高15.1 m,总厚4.2 m,其中,单片墙肢厚度为0.6 m。反力墙B正面以隔墙为分界线,分为五个加载区,加载孔布置方式同反力墙A。试验台座采用箱型地锚式台座,长46.8 m,宽23.9 m,高3.8 m。顶板均匀布置锚孔,定位与反力墙加载孔定位对齐,基本可满足固定任意尺寸的加载模型。为充分利用实验室空间和原有加载设施,满足更多试验的需要。反力墙A一侧设置为滑槽式台座,由反力墙A的侧面提供水平加载力,试验结构可沿台座的纵向任意移动,液压加载装置可沿槽道上下任意移动,从而适应试验结构加载位置的灵活性[3]。反力墙B的背面临振动台,并且背面布置部分加载孔,可为振动台上的试验结构提供水平加载力。反力墙系统的实体模型见图1,反力墙A立面图见图2。
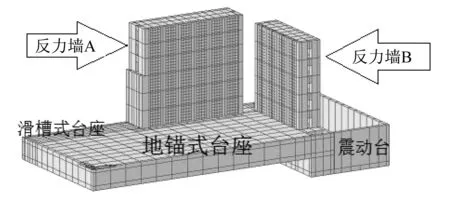
图1 反力墙系统的实体模型Fig.1 Entity model of reaction wall system
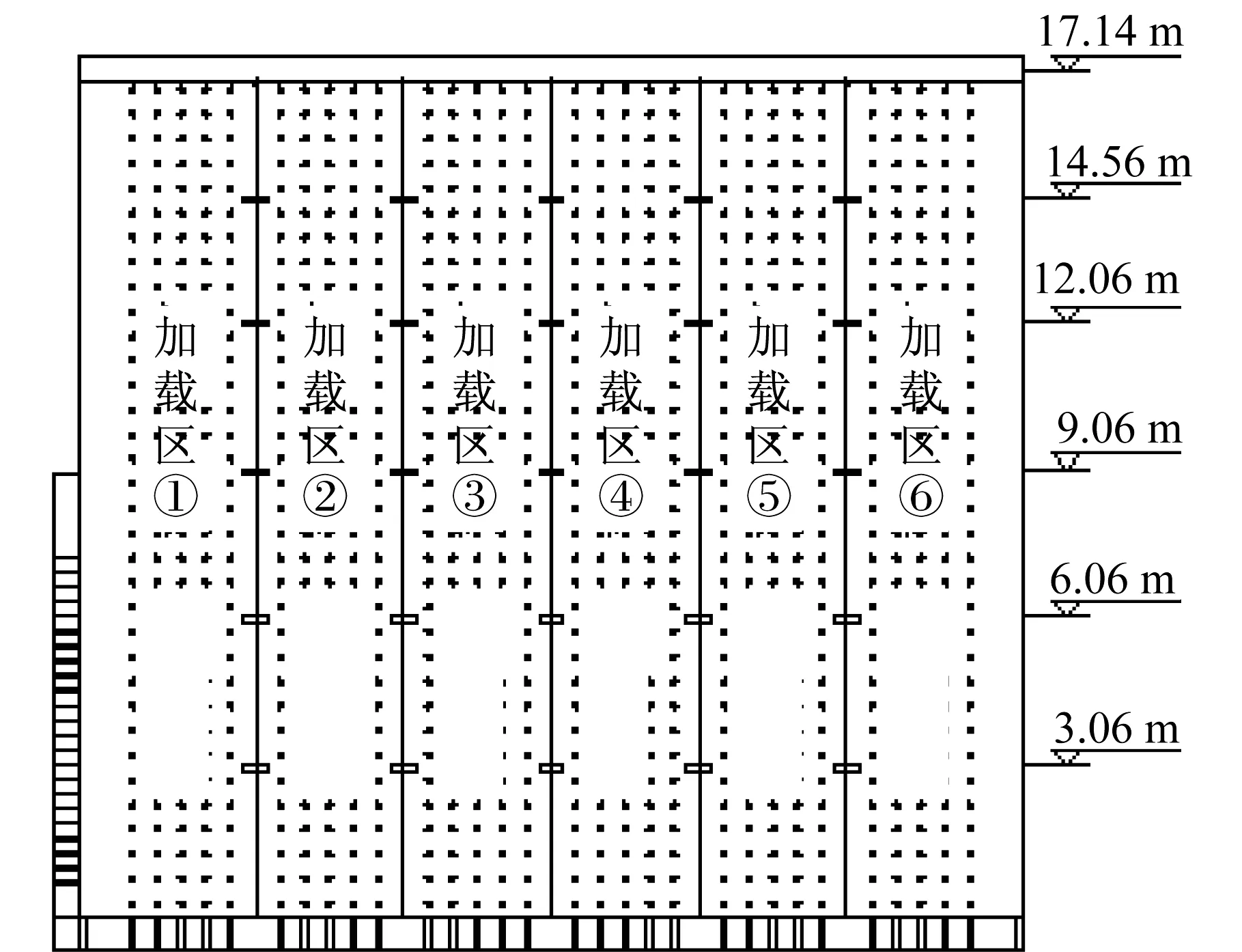
图2 反力墙A立面图Fig.2 Elevation of reaction wall A
2 有限元分析
2.1 设计要求
反力墙按多层整体结构抗震试验(低周反复试验或拟动力试验)进行荷载设计,主要为平面外荷载,各层加载峰值见图3,呈倒三角形式。平面内荷载包括反力墙A给滑槽式台座上的模型提供的水平加载力,加载值较小,且反力墙平面内刚度较大,设计时,平面内荷载不考虑。反力墙A对五层足尺寸模型施加水平力,反力墙B对四层足尺寸模型施加水平力。反力墙单孔最大承载力为400 kN,地锚式台座单孔竖向最大承载力为400 kN,水平最大抗剪承载力为250 kN。
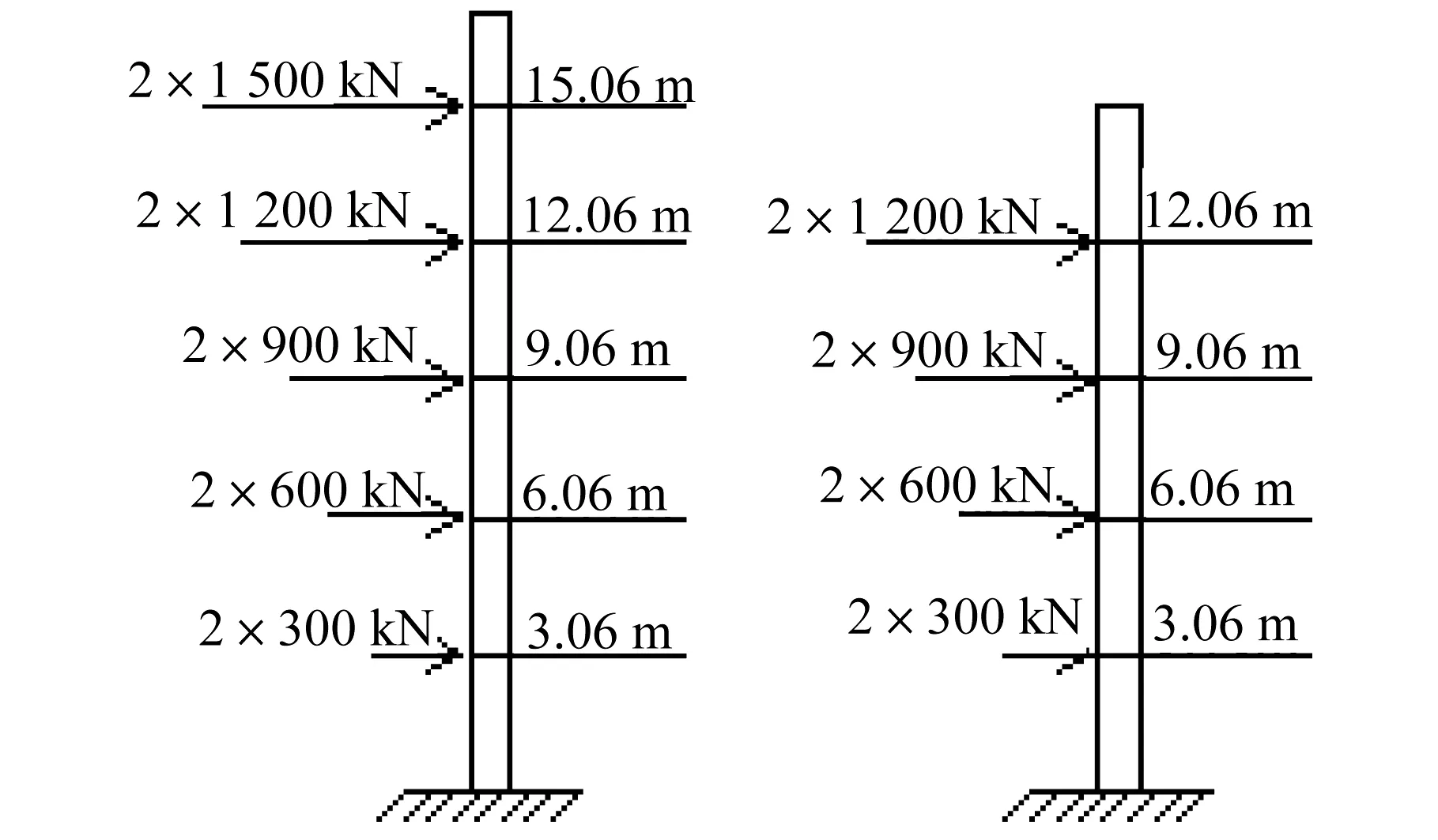
图3 设计荷载形式Fig.3 Diagram of design load distribution
2.2 控制条件
反力墙在正常使用中承受较大水平荷载,水平方向的挠度直接影响试验构件的试验精度,因此,反力墙水平方向挠度的控制是设计中最重要的控制条件[1]。同时,为保证反力墙的正常使用极限状态,需要控制其最大裂缝宽度。挠度和裂缝宽度的控制,可使反力墙不会因产生较大的附加变形而影响试验精度。
(1) 满负荷时,反力墙顶点的最大位移控制在墙高的1/4 000内。
(2) 反力墙结构的裂缝控制等级介于二级和一级之间,即
σck-σpc<0.8ftk
式中:σck为荷载标准组合下抗裂验算边缘的混凝土法向应力;σpc为扣除全部预应力损失后,在抗裂验算边缘的混凝土的预压应力;ftk为混凝土的轴心抗拉强度标准值。
2.3 单元类型和模型边界条件
由于反力墙墙肢及肋墙的厚度较大,体积量占反力墙总体积的比值较大,故采用三维实体单元建立有限元模型进行分析可以得到最精确的结果。Midas/Gen中的实体单元形状有楔形、三角棱柱体和六面体,采用六面体单元可以得到较为准确的位移和应力结果[4]。故采用六面体来模拟混凝土。预应力筋的布置采用实体力筋法,将混凝土和预应力筋划分为不同的单元一起来考虑。Midas/Gen中,预应力的模拟可以对桁架单元施加初拉力,此处为张拉控制应力扣除预应力损失后的有效预应力。仅仅将桁架单元两端与实体单元共节点,不考虑桁架单元和实体单元之间的粘结与滑移,这样,可以直观、真实地模拟无粘结预应力钢绞线[5]。
反力墙系统有限元模型采用与反力墙实际相同的边界条件,对试验台座底部节点施加所有方向的位移约束。试验台座周围施加弹性支撑,模拟台座与周围土体的接触关系。弹性支撑的刚度由地质勘查资料提供的数据参考JTG D63—2007《公路桥涵地基与基础设计规范》提供的非岩石地基水平向抗力系数的比例系数m换算得到。
2.4 材料参数及混凝土的本构关系
试验台座、反力墙及基础均采用现浇钢筋混凝土,混凝土强度等级均为C40,弹性模量Ec=3.25×104N/mm2,泊松比v=0.2,密度ρ=25 kN/m2,钢筋均为HRB400级。为有效控制墙体裂缝的出现,采用后张无粘结预应力钢绞线UPS15.2-1860,1×7(7股)型,张拉控制应力σcon=0.75fptk=1 395 N/mm2。
混凝土的本构关系主要有线弹性、非线弹性、弹塑性及其他力学理论四类。反力墙系统的分析采用线弹性全量型模型[6],即应力和应变在加载和卸载时呈线性关系,其表达式为
σ=Eε
(2)
2.5 加载条件
任意两个相邻加载区,容许同时加载。
工况:
(1) 荷载作用在加载区①和加载区②;
(2) 荷载作用在加载区②和加载区③;
(3) 荷载作用在加载区③和加载区④;
(4) 荷载作用在加载区④和加载区⑤;
(5) 荷载作用在加载区⑤和加载区⑥。
荷载作用形式:
(1) 按倒三角的形式进行荷载布置,层高为3 m,两列荷载横向相距3 m,见图4(a)。
(2) 将倒三角荷载按底部弯矩等效折算到顶部。即反力墙A在15.06 m高处作用2×3 300 kN的集中力,相距3 m,见图4(b)。
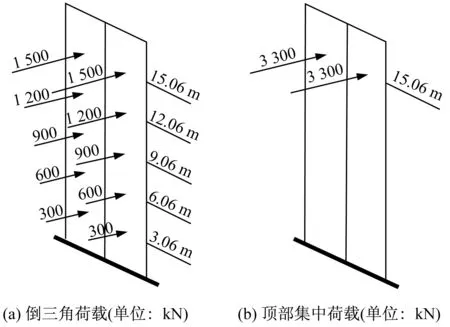
图4 荷载作用形式示意图Fig.4 Diagram of load distribution
为避免由于施加集中力而使结构在有限元建模分析时发生应力集中和不收敛,将各集中荷载转化成面荷载作用在120 mm×250 mm的单元表面。实际使用中,液压千斤顶与反力墙混凝土之间是有一定接触面的,转化成面荷载作用,更接近实际。
2.6 计算结果分析
由Midas/Gen计算得到各工况下的应力云图,例如工况5的应力云图(图5),得到各工况下的最大拉应力和最大压应力(表1)。拉压应力均是沿Z轴方向的应力,其中,负号表示压应力。整体结构的最大压应力为-6.136 N/mm2,出现在反力墙背面的墙体上,远小于混凝土抗压强度标准值。反力墙A在任意两个相邻加载区施加荷载,反力墙正面与台座表面相交的部位出现最大拉应力,并且荷载位置不同,最大拉应力的值也不同。工况1和工况5取得的最大拉应力值较大(分别在D点和E点取得最大值),工况3取得的最大拉应力值较小(在E点取得)。经过分析,荷载作用在两端时,扭转变形对墙身底部的应力产生了较大的影响。混凝土抗拉强度标准值ftk为2.39 N/mm2[7]。在无预应力作用时,各工况下的最大拉应力超过限值1.92 N/mm2(0.8ftk)。施加预应力,对降低反力墙拉应力起到了一定作用。但荷载作用在两端时的最大拉应力均仍超过限值1.92 N/mm2。由表中数据可得,各工况下顶部集中荷载作用产生的最大拉应力小于相应倒三角荷载作用时产生的最大拉应力,所以,从安全、经济的角度出发,当反力墙有较大荷载作用时,其作用位置应引起注意,3.7节中做进一步讨论。
表1反力墙A的应力计算结果(无预应力/有预应力)

Table 1Stress calculation results of reaction wall A (without/with pretension)
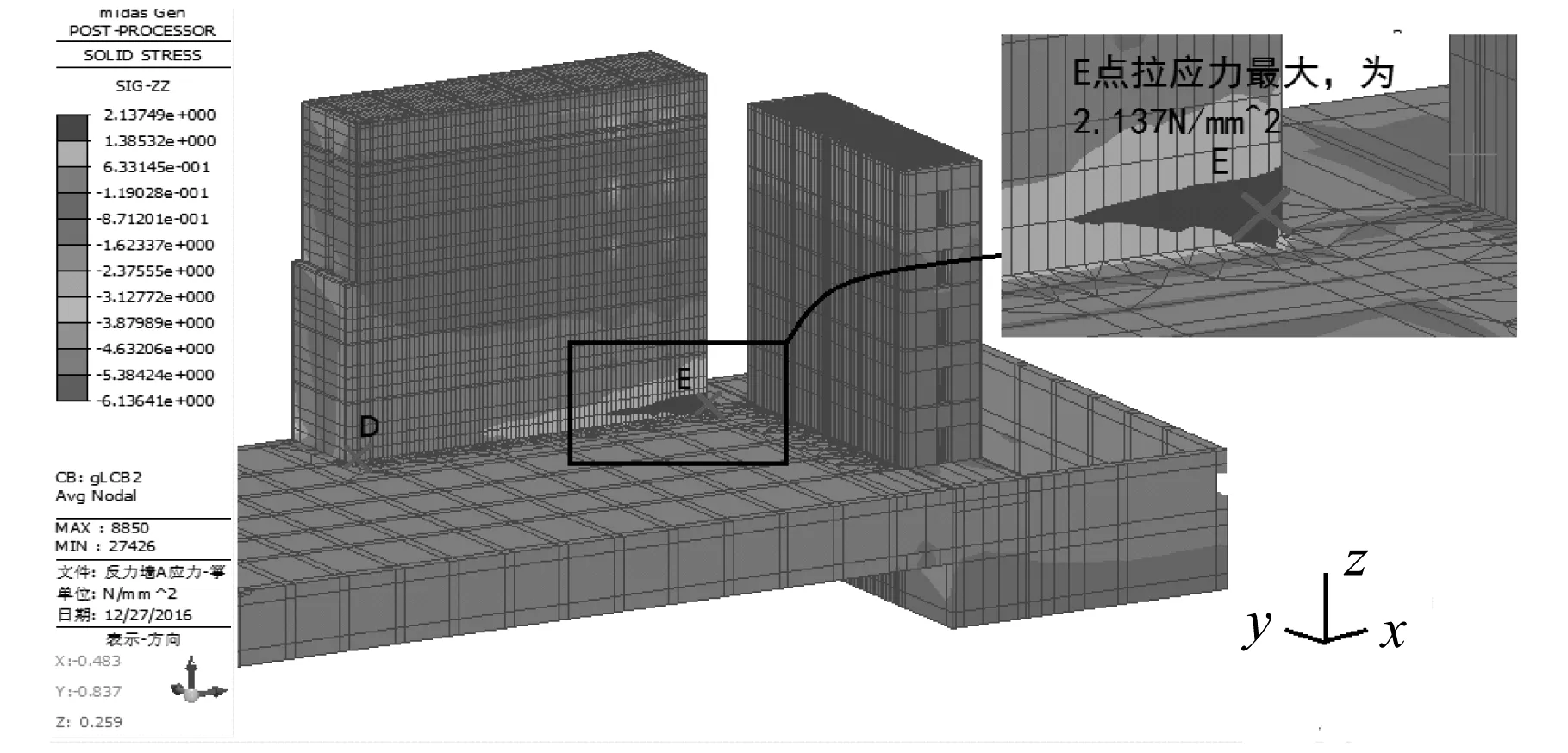
图5 工况5在倒三角荷载作用下的应力云图Fig.5 Stress contours of 5th working condition under inverted triangle loads action
由Midas/Gen计算得到各工况下的位移等值线,如工况5的位移等值线(图6),得到反力墙A在各工况下的最大位移(表2)。反力墙A在任意两个相邻加载区施加荷载,最大位移呈两端大中间小的规律,即荷载位于两端时的最大位移更大,反力墙发生了较大的扭转变形[8]。当荷载作用在加载区⑤⑥时,倒三角荷载作用下在高度为17.14 m的C点取得最大位移3.467 mm;集中荷载作用下在高度为17.14 m的C点取得最大位移3.540。二者均小于限值4.285 mm (H/4 000)。
表2反力墙A在各工况下的最大位移及位置(mm)

Table 2Maximum displacement and position of reaction wall A under various working conditions

图6 工况5在倒三角荷载作用下的位移等值线Fig.6 Displacement contours of 5th working condition under inverted triangle load action
2.7 实用性研究
结合上述分析结果,将工况1和工况5作用荷载适当降低。考虑到试验的多样性,不同的试验可能作用不同大小、不同形式的荷载。为方便反力墙的使用,得出基于实际使用情况的各点最大允许荷载包络图。
情况一,考虑到部分试验需要较大的单点加载力,而反力墙单孔最大承载力为400 kN,所以,实际使用时,可使用强度和刚度较大的垫板将加载力分散到多个加载孔。模拟两个试验同时进行单点加载,每个试验的单点加载力不得大于反力墙对应合力作用点的最大承载力,各点最大容许荷载见图7。例如,试验一和试验二同时进行单点加载(图8),试验一用垫板M将加载反力分散到12个加载孔,加载力作用点位于板M形心处,最大加载力由图7得到,为5 350 kN;试验二用垫板N将加载反力分散到9个加载孔,加载力作用点位于板N形心处,最大加载力由图7得到,为2 800 kN。两个实验加载力作用点间距不得小于3 m。图7中,9 m以下承载力包络图未画出,原因是考虑实际情况和9 m以下墙体的承载能力,基本可满足各试验加载要求。在实际使用中,应根据各试验所需的加载力大小选择模型相对于反力墙的位置,既保证反力墙可提供给模型足够的加载力,也保证反力墙的安全性。
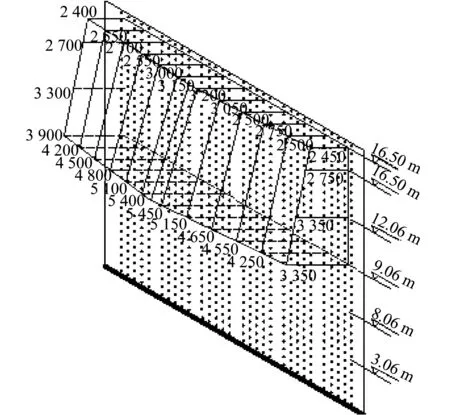
图7 容许荷载包络图Fig.7 Envelope diagram of allowable loads
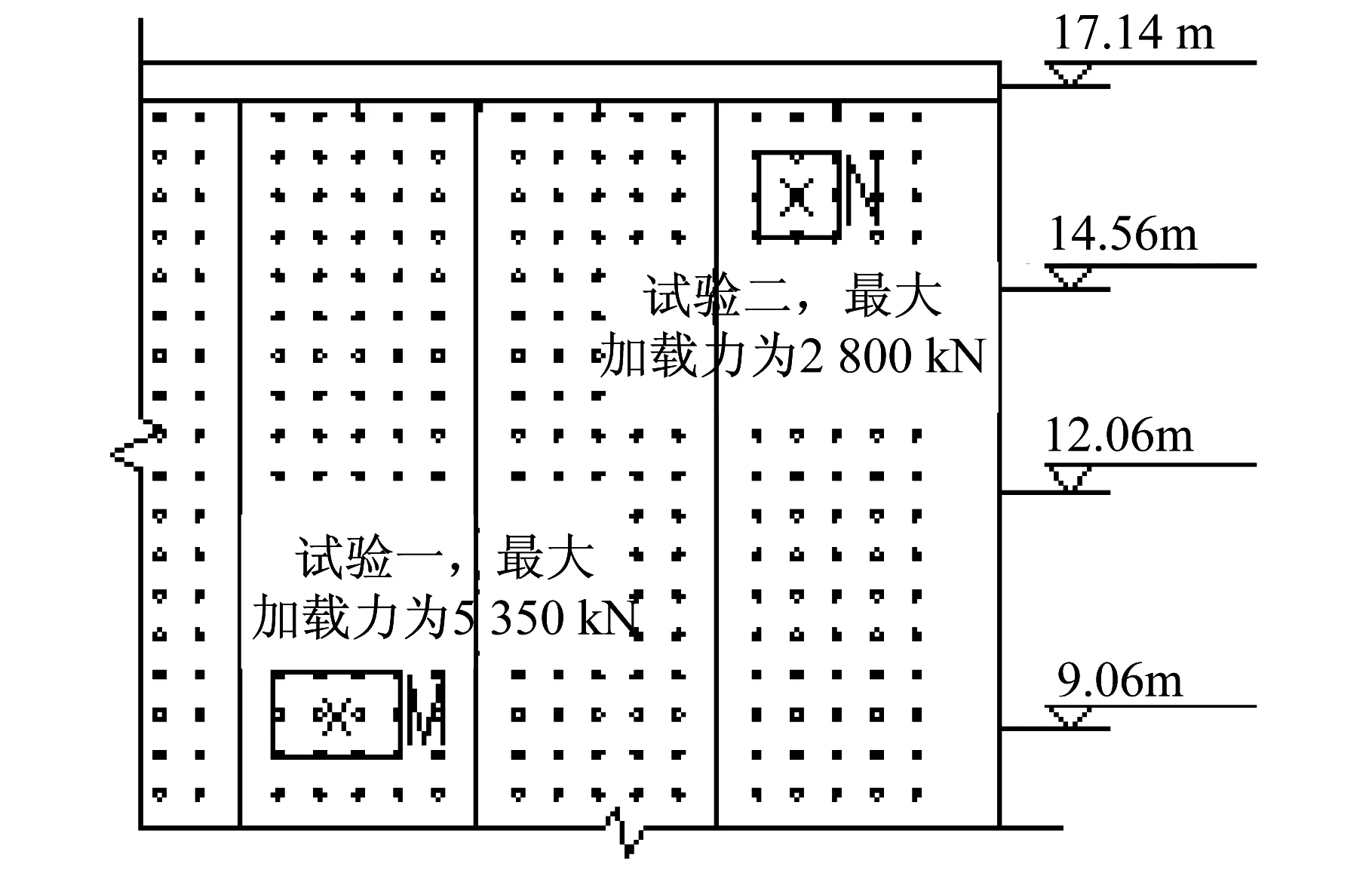
图8 试验示意图Fig.8 Diagram of test
情况二,模拟对某结构顶部作用一对集中力(2F),间距为3 m,加载点位于不同的部位,可提供的最大加载力不同,见图9。若结构加载力为间距3m的倒三角形式的荷载,则将其折算为最高作用位置的集中力进行判定是否合适。
图9解释说明:反力墙A的每个加载区包含a、b、c、d四列,相邻加载区中的同一字母表示的列相距3 m,所以,在某一高度,荷载可作用在相邻加载区同一字母表示的位置。例如图9(a)中M点,表示某结构在高度为12.06 m的位置作用一对间距为3 m的集中力(2×F),一个力作用点位于加载区①的a列,另一个力作用点位于加载区②的a列,则其最大加载力F为3 400 kN。M点荷载作用示意图见图10。
3 结 论
本文采用Midas/Gen软件对某预应力反力墙系统进行有限元建模,分析了各工况下的受力和变形,得到以下结论:
(1) 反力墙的扭转效应不可忽略。荷载位于反力墙两侧时,反力墙会发生较大的扭转变形,既增大了反力墙底部的拉应力,同时也增大了反力墙的位移。
(2) 反力墙不同部位的最大承载力不同。同一水平线上,中间大,两端小。为充分发挥反力墙的能力,绘出各点最大容许荷载包络图,为反力墙的使用提供依据,为反力墙的优化设计提供参考。
