集流器结构对多翼离心风机气动性能的影响

魏铭,熊仲营,刘小民,孙利校

(1.西安交通大学能源与动力工程学院,710049,西安;2.杭州德意电器股份有限公司,311215,杭州)

多翼离心风机以其尺寸小、压力系数大、流量系数高、噪声低的特点被广泛地应用于家用空调、吸油烟机及通风换气装置中。随着人们居住环境的改善和生活品质的提高,对厨房内吸油烟机性能的要求也越来越高。多翼离心风机作为吸油烟机的核心部件,直接决定了吸油烟机的性能好坏,越来越受到科研工作者和生产企业的关注。

集流器、蜗壳、叶轮是多翼离心风机重要的三大部件,研究人员对多翼离心风机的叶轮和蜗壳进行了较为详细的研究和优化设计[1-5],关于集流器的研究相对较少,然而有研究表明,作为多翼离心风机进口导流装置的集流器对多翼离心风机的气动性能有着较大程度的影响[6-7]。Lee等在CFD数值模拟的基础上,对集流器与叶轮之间具有不同间隙大小的离心风机内部流场进行了分析比较,指出如果集流器与叶轮之间的间隙选择不合理,将导致风机整体性能下降2%～5%[8]。王嘉冰等采用CFD方法,对3种不同结构形式集流器的柜式空调用多翼离心风机的性能进行了数值计算,得出了集流器出口截面直径大于叶轮内径的收敛型集流器能使风机气动性能达到最优的结论[9]。许文明等对柜式空调用多翼离心风机集流器进行研究,表明集流器的不同结构形式及其出口到叶轮的距离对整机的气动性能影响较大,经过优化的集流器能够使循环风量在增加4.7%的情况下而噪声不增大[10]。赵燕杰等通过对离心风机的集流器扩张角、集流器收缩角和扩张段长度的参数化研究,指出锥弧形集流器对离心风机气动性能较为影响显著,但对声功率级的影响不显著[11]。考虑到离心风机进气的不对称性,部分学者也研究了偏心集流器对多翼离心风机气动性能的影响[12-14]。温选峰等通过实验研究表明,具有合理参数和安装位置的椭圆形集流器能够有效提高多翼离心风机的整体气动性能[15]。

本文以某型号吸油烟机用多翼离心风机为研究对象,首先采用CFD方法对带有原型集流器的多翼离心风机进行了数值模拟,并通过实验验证了数值模型和数值方法的有效性。然后,通过改变集流器的设计参数,研究集流器出口直径和轴向间隙对多翼离心风机气动性能的影响及其贡献度。

1 数值计算

1.1 控制方程

流体运动遵循物理守恒定律,这些守恒定律的基本方程包含质量守恒方程、动量守恒方程和能量守恒方程。因为本文研究的多翼离心风机在模拟计算时不考虑热交换的问题,所以只涉及质量守恒方程与动量守恒方程的求解。

质量守恒方程即连续性方程,在直角指标系下,其微分形式的表达式为

(1)

式中:ρ为流体密度;t为时间;u为流体速度。吸油烟机用多翼离心风机内流动速度一般不超过30 m/s,因此可以假设为黏性不可压缩流动,不考虑密度变化的影响。

动量守恒方程的物理本质是牛顿第二定律,在直角坐标系下,其数学表达式的微分形式为

(2)

式中:Σ为应力张量;f为流体微元所受体积力。

将动量守恒方程带入流体力学的本构方程,得到Navier-Stokes方程

(3)

式中:p为流体微元上的压力;μ为动力黏度;S为应变率张量。

对连续方程和动量方程进行时间平均,得到雷诺时均Navier-Stokes方程,由于进行了时均化处理,会导致原有的方程组不封闭。以湍流的理论、试验数据或数值计算结果为基础,通过对雷诺应力做出假设,提出湍流模型方法是一种常见的解决方法。对于湍流计算,本文采用基于雷诺平均的Realizablek-ε模型,相应的湍动能k与湍动耗散率ε的方程为

(4)

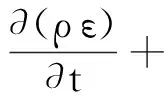
(5)

式中:μt为湍流运动的黏性系数;σk、σε为k、ε基于湍流流动的普朗特准则数;Gk为k-ε模型生成项;C1、C2为经验常数;ν为运动黏度。

1.2 计算模型及网格划分

本文研究的多翼离心风机为双进气形式,应用于吸油烟机中,其蜗壳、叶轮及相应的集流器结构如图1所示,风机的主要结构参数如表1所示。

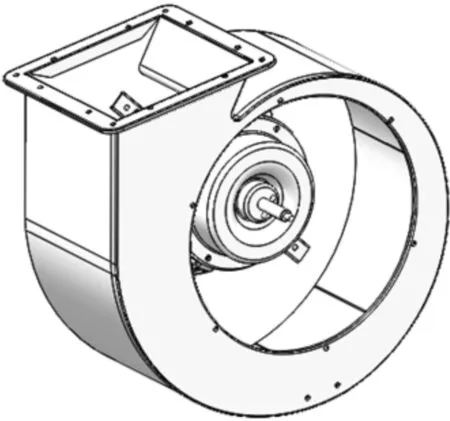
(a)蜗壳

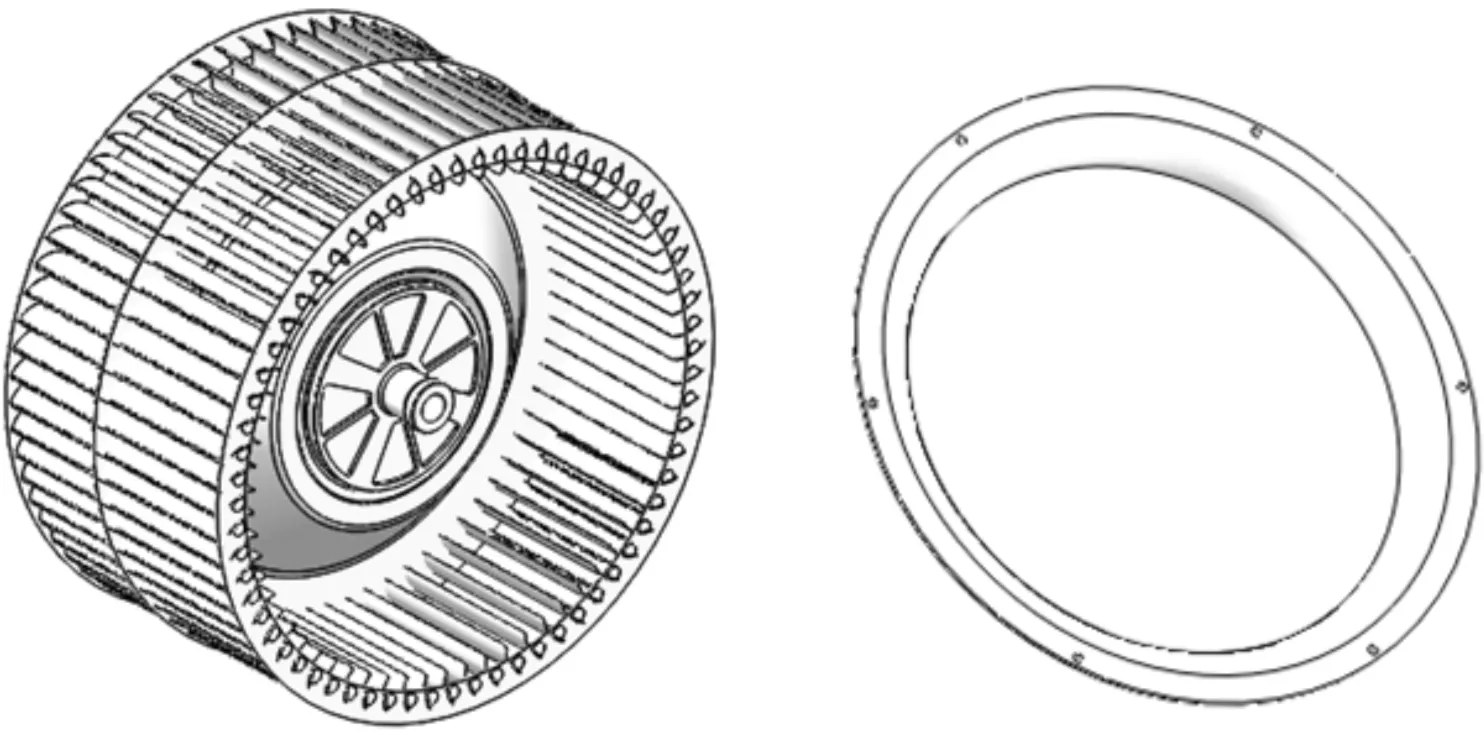
(b)叶轮 (c)集流器图1 双进气式多翼离心风机结构

采用Solidworks和ICEM CFD分别对多翼离心风机进行数值计算流场区域的三维建模和网格划分,其中多翼离心风机进口向上游延伸长度为一倍的叶轮外径,风机出口向下游同样延伸长度也设置为一倍的叶轮外径,数值计算模型如图2所示,对于叶轮、蜗壳、进出口延伸段分别进行了网格划分。为了保证数值计算的准确性,在网格划分时,对近壁面处网格进行了加密处理,并进行了网格无关性验证,最终数值模拟的多翼离心风机计算模型的网格数约为400万。

采用CFD商业软件Ansys Fluent 16.1对多翼离心风机气动性能及其内部流场进行数值计算。由于吸油烟机用多翼离心风机的性能测试是在实验室进行的,工作介质为空气。为了与实验测量结果进行比较,数值计算中模拟的工作介质仍为空气,密度设定为标准状态下的空气密度。另外,多翼离心风机的进口雷诺数Re>12 000,属于湍流流动。考虑到多翼离心风机内部流动的不可压缩性及其流动的复杂性,湍流计算采用能够较为准确模拟漩涡流动、边界层流动及分离流动的Realizablek-ε模型。压力-速度的耦合采用SIMPLE算法,压力离散格式采用PRESTO!格式,动量方程、能量方程、湍动能控制方程以及湍流耗散方程中的对流项均采用二阶迎风格式。流体运动连续方程中X、Y、Z这3个方向上的速度分量以及湍流计算中的k、ε的收敛残差均设为10-4。给定的边界条件为:①将叶轮区域设置为旋转区域,叶轮沿Z轴逆时针转动,旋转速度根据电机在不同工况点的实际转速给定,其他区域设置为静止区域,动静交界面采用MRF参考系模型;②将叶轮叶片壁面采用相对坐标系,相对于叶轮旋转区域静止,风机其他壁面为绝对静止面;③进口给定压力进口边界条件,总压为0;④出口给定压力出口边界条件,静压根据实验测得的不同工况点的压力值进行设定。

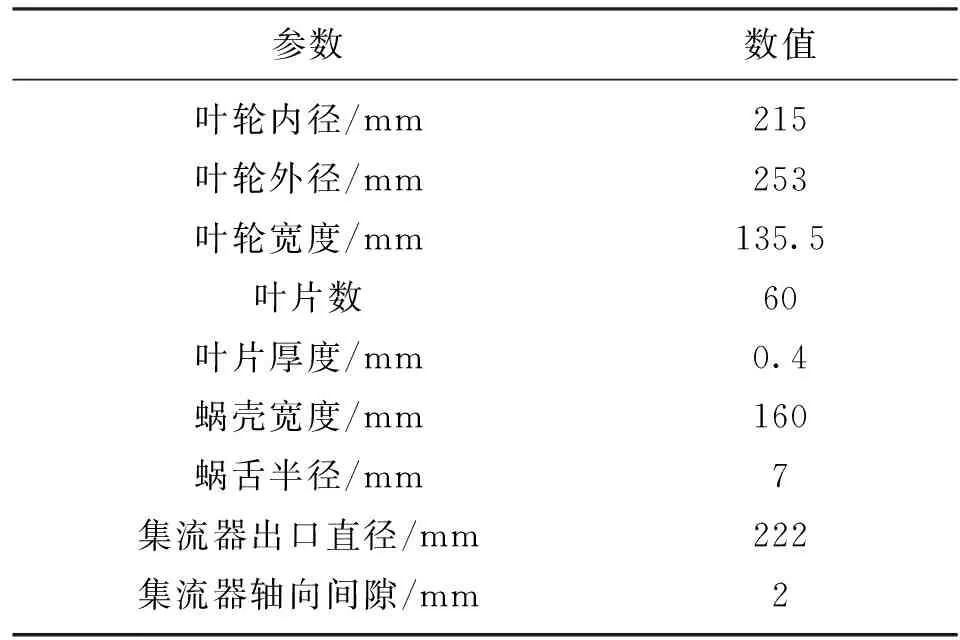
表1 多翼离心风机基本设计参数

图2 多翼离心风机数值计算模型

1.3 实验测量

本研究中采用的气动实验装置的有关要求按照GB/T 17713—2011附录C《外排式吸油烟机空气性能试验方法》和GB/T14806—2003《家用和类似用途的交流换气扇及其调速器》的规定执行。风机出风口端实验测量在减压筒中进行,如图3所示,根据减压筒中测试点测得的静压,计算出风机的流量,再根据空气参数计算出多翼风机在连接器处的标准静压,即计算模型中出口处的静压。实验规定空气性能实验环境温度为(20±5) ℃,相对湿度不大于85%,环境气压为一个标准大气压,实验同时无外界气流影响以及热辐射影响。为了提高实验的准确度,被测风机在额定电压及额定频率下工作,在实验装置上稳定运行1 h之后再进行测量。

图3 风机性能测试装置示意图

气动性能测试实验台按照国标要求设置,其中风机出风口通过连接器与空气性能实验装置相连,通过连接器的气流依次通过十字整流器、扩散段后进入减压筒,最后通过变直径孔板后流出。在此过程中,通过数据采集装置测得不同孔板直径下的气动性能数据,通过计算机储存数据计算得出试验结果,包括各个工况点下的风量、全压、静压、全压效率等性能参数。数值模拟过程中设定的叶轮旋转速度与气动性能测试过程中每个工况点的实时转速相同,风机噪声的测量在杭州德意电器股份有限公司的半消音噪声实验室进行。

1.4 实验与计算结果比较

本文对实验测量中的部分运行工况点进行了数值模拟,计算结果与实验测量的流量-静压性能曲线如图4所示。由图4可知,数值模拟的7个工况点与实验测量值吻合较好,表明本文的数值计算模型及计算方法是有效的。在零静压工况条件下,风机最大风量计算值与模拟值分别为17.57、18.01 m3/min,相对误差约为2.2%;在最大效率工况条件下,风机计算静压与实验测量静压分别为302.21、301.04 Pa,相对误差约为0.3%。随着出口静压的升高,风机的实测流量与计算流量呈现非线性下降。在小流量工况条件下,由于出口的回流增大,计算值与实验值之间的误差也相应增大。计算曲线和实验曲线的变化趋势基本一致,因此当流量小于4 m3/min时,尽管由于流动分离严重、数值计算失效,但相关的计算工况点可以根据已有计算结果进行外插值方法获得。

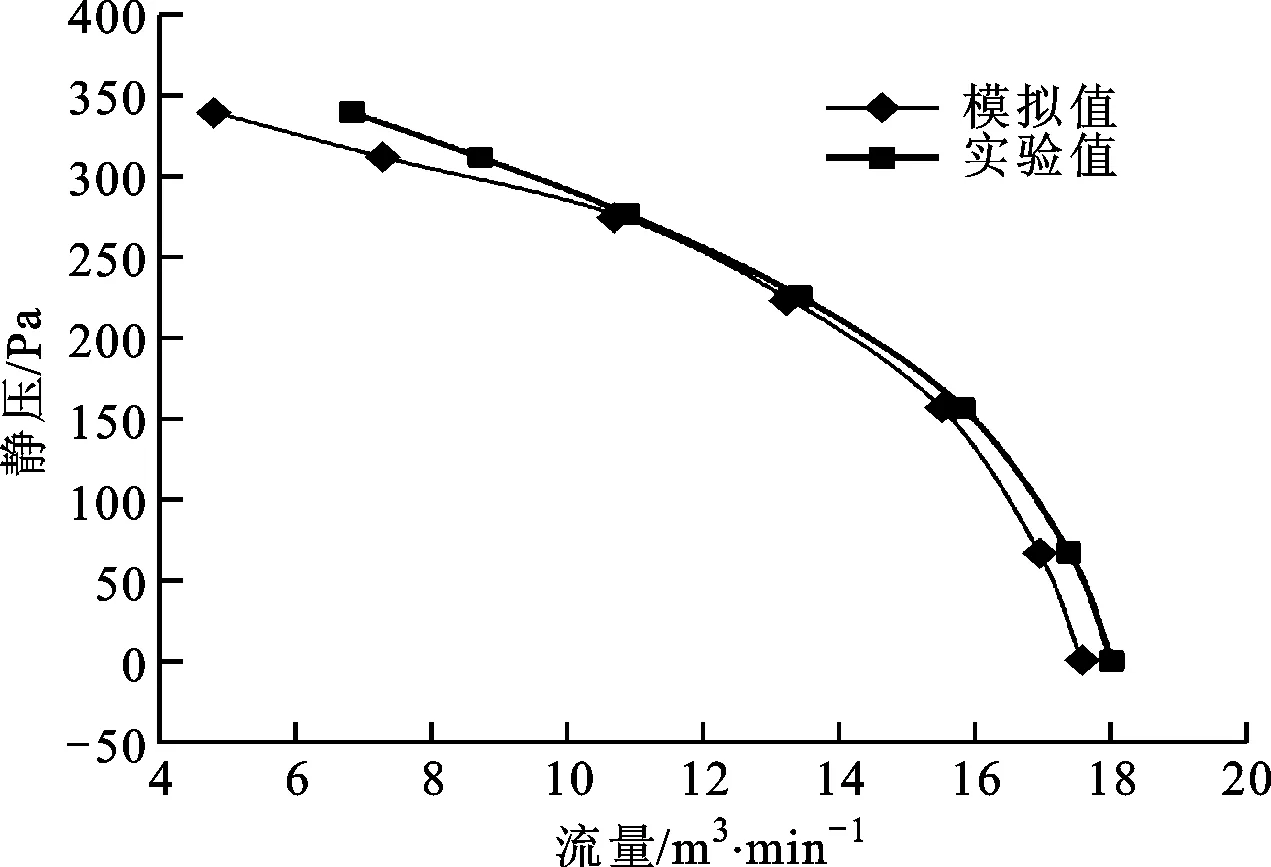
图4 多翼离心风机流量-静压性能曲线

2 集流器优化

2.1 集流器改进方案

由于影响多翼离心风机气动性能的结构参数较多,例如叶轮参数、蜗壳型线、蜗舌形状,集流器参数等,并且这些参数存在一定的耦合影响关系,本文研究主要是针对多翼离心风机的集流器结构进行优化。根据研究对象,集流器的主要结构参数有轴向间隙δ、圆弧半径Rin、集流器高度h、集流器进口直径di及集流器出口直径do,如图5所示。

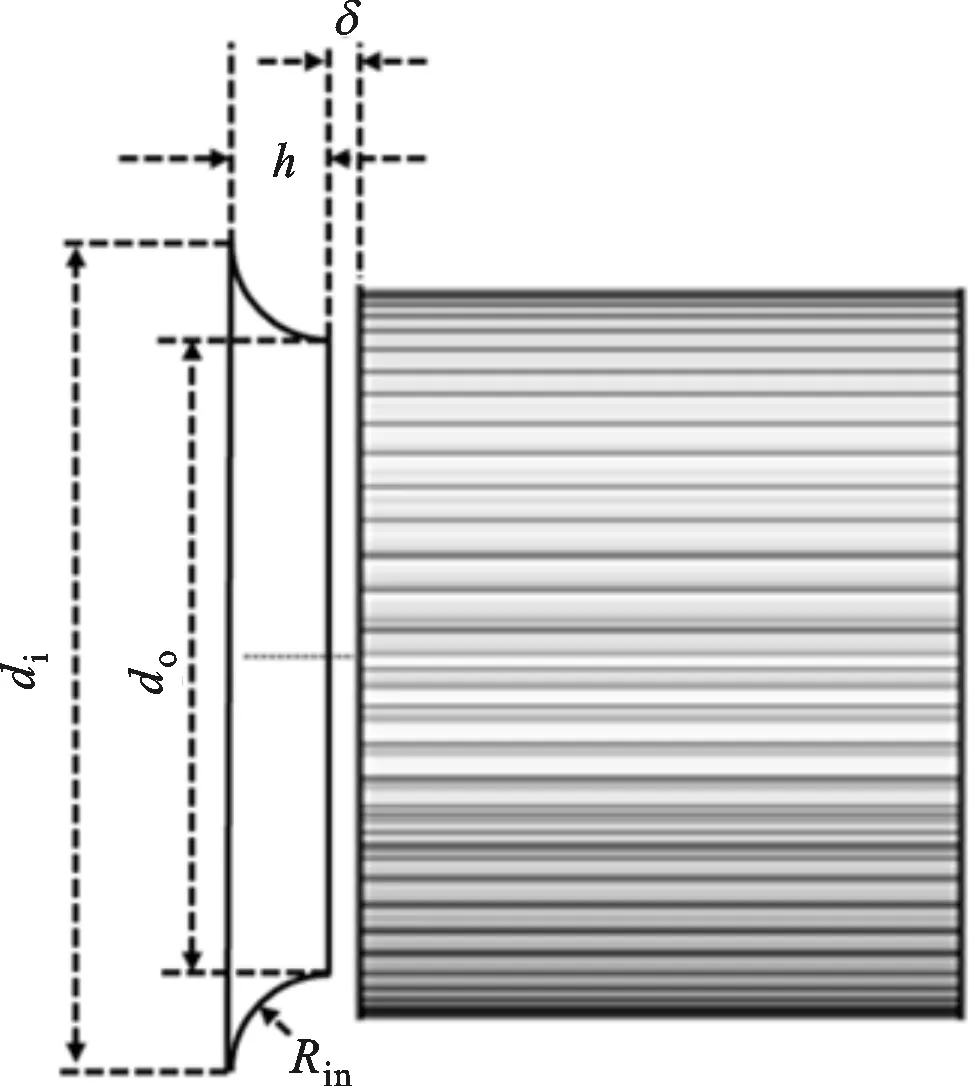
图5 集流器结构参数示意图

集流器对多翼离心风机的主要影响参数包括轴向间隙、集流器出口直径以及集流器圆弧形状等,但对于吸油烟机用多翼离心风机而言,由于还涉及到吸油烟机箱体结构的影响,因此这里只选取集流器出口直径do和轴向间隙δ作为优化设计参数,采用DoE(design of experiments)方法来研究集流器结构参数对多翼离心风机性能的影响。对每个参数选择了3个水平,基于Solidworks软件,建立了9个数值计算模型,每个模型的具体参数如表2所示,其中计算模型3为原型风机。

表2 集流器结构参数

对于建立的集流器模型,本文选取了两个工况点进行数值分析,这两个工况点分别对应着多翼离心风机的最高效率点和最大流量点。

2.2 计算结果分析

为了便于比较不同集流器对风机空气性能和内部流动的影响,这里选取风机的最大流量点的流量Q0、容积效率ηv、全压P0,最高效率点的流量QBEP、内效率ηBEP来比较不同参数设计条件下风机的气动性能。风机ηv、ηBEP的计算式为

%

(6)

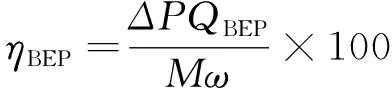
(7)

式中:Qinlet为风机进气口流量;Qimp为叶轮进口流量;Qgap为叶轮与集流器间隙泄露流量;ΔP为风机在最高效率点的全压升;QBEP为风机最高效率点流量;M为风机在最高效率点的扭矩;ω为风机在最高效率点的转速。叶轮与集流器之间的流量分布如图6所示。

图6 集流器与叶轮间流量分配示意图

为了使研究结果更具普遍性,对性能参数进行无量纲化处理。采用相对指标来进行性能的比较和分析,相对指标定义为

(8)

式中max(I)为性能参数I的最大值。

2.2.1 集流器出口直径的影响和贡献度 通过对不同集流器结构设计参数的多翼离心风机模拟的数值模拟,本文研究获得了不同集流器设计参数下的多翼离心风机的气动性能及其对性能影响的贡献度。图7所示为轴向间隙δ=2 mm时,不同集流器出口直径do对风机性能的影响。由图7可知:风机的最大流量点的流量和全压随着集流器出口直径的减小而增加,且增加量在222～214 mm之间;当do为206 mm时,最大流量和全压都得到了显著提升,相比do=222 mm时的风机流量提升了9.0%,全压提升了18.2%,但最大流量点的容积效率却在do=206 mm时最小;在最高效率点,随着出口直径的减小,其流量和内效率都有较小幅度的提升。

图7 δ=2 mm时不同do下的性能对比

图8 δ=6 mm时不同do下的性能对比

图8为轴向间隙δ=6 mm时,不同集流器出口直径对风机性能的影响。由图8可知:当轴向间隙δ=6 mm、do=206 mm时,可以提高风机在最大流量点的流量和全压以及在最高效率点的流量和内效率;当do=206 mm时,风机集流器与叶轮之间的轴向间隙的增大,使得风机的容积效率低于集流器出口直径do为214、222 mm时的风机。

图9所示为轴向间隙δ=10 mm时,不同集流器出口直径对风机性能的影响。由图9可知,当轴向间隙δ=10 mm时,集流器出口直径仍在do=206 mm时,风机的性能较优,但性能提升的幅度明显小于轴向间隙δ为2、6 mm时的提升幅度,这说明轴向间隙的变化会对风机的性能产生影响,且有可能会改变其他参数对风机性能影响的程度。

图9 δ=10 mm时不同do下的性能对比

由图7～9可知,在相同轴向间隙条件下,多翼离心风机的最大流量在研究尺寸范围内随出口集流器直径的减小而增加,这说明叶轮对气体的做功能力与集流器出口直径有关,这种关系主要由叶轮内径与集流器出口直径的相对大小确定。由于轴向间隙的存在,进入风机的气流会从蜗壳内部压力较高的区域泄露至叶轮进口压力较低的区域,从而对集流器出口气流造成影响。当集流器出口直径大于叶轮内径时,由于风机叶轮前盘的存在,集流器出口气流直接撞击叶轮前盘,在风机进口处形成旋流,风机流量减小;当集流器出口直径与叶轮内径相当,集流器与叶轮间的泄露气流会对集流器出口主气流产生冲击,使得风机流量减少;当集流器出口直径小于叶轮内径时,这时泄露气流对集流器出口主气流的影响并不明显,叶轮进口气流分布更为均匀,从而增大了风机流量。

2.2.2 集流器轴向间隙的影响和贡献度 在相同轴向间隙时,从不同集流器出口直径时得到的性能参数可以看出,当集流器出口直径do=206 mm时,风机可以获得最优的气动性能。本文仅对do=206 mm时,轴向间隙不同的风机模型进行研究,不同δ下的性能对比如图10所示。由图10可知:在最大流量点,当轴向间隙由2 mm增大到6 mm时,风机的风量、全压和容积效率基本保持不变;当轴向间隙增大到10 mm时,风机的风量、全压和容积效率均有较大幅度的下降。在最高效率点,对于不同的轴向间隙,风机的内效率变化不大,当轴向间隙为6 mm时,风机的风量达到最大。这表明轴向间隙过小时,虽然可以减小叶轮与集流器间隙泄露流量,但同时会减少叶轮的做功能力,使得风机的风量减小;轴向间隙过大时,虽然叶轮的做功能力增加,但由于叶轮与集流器之间的间隙泄露流量增加,使得风机的风量减小。这也表明,对于多翼离心风机的集流器轴向间隙与出口直径之比存在一个最佳值,这个无量纲参数应作为集流器的重要设计参数而引起设计者的重视。

图10 do=206 mm时不同δ下的性能对比

通过结果分析,集流器轴向间隙的大小会对多翼离心风机的气动性能产生影响,当轴向间隙由2 mm增加到6 mm时,风机的气动性能得到了一定程度的提升。但当轴向间隙继续增加到10 mm时,风机的气动性能却明显下降,这表明多翼离心风机的轴向间隙存在一个最佳取值。

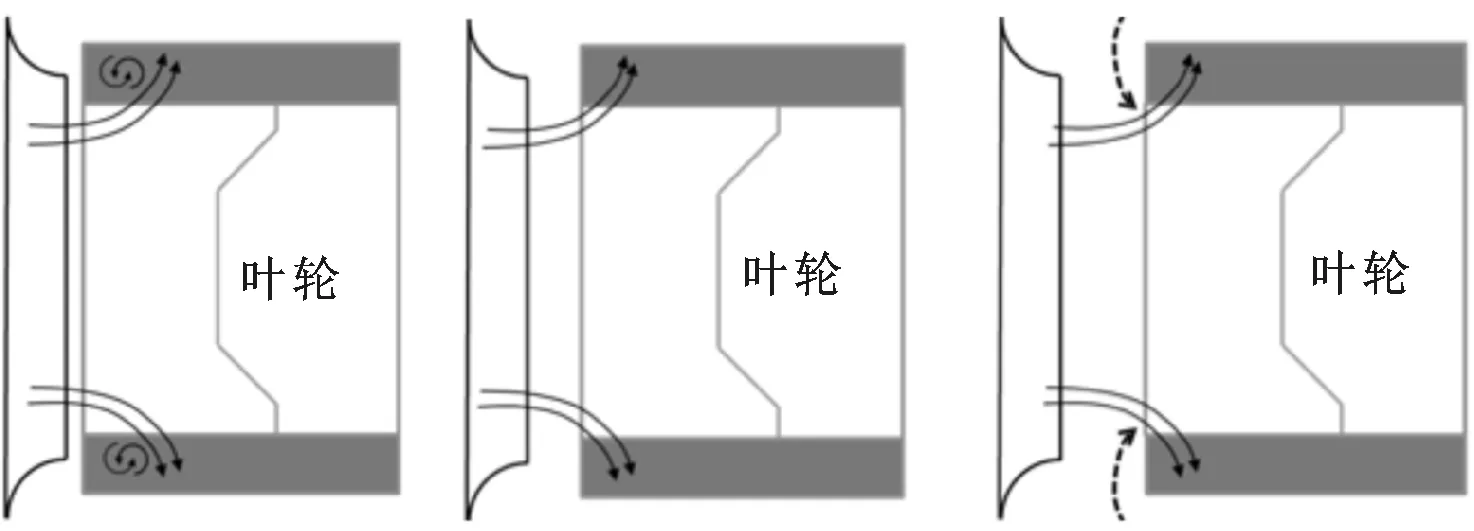
(a)间隙过小 (b)间隙适中 (c)间隙过大图11 集流器轴向间隙对多翼离心风机性能影响的示意图

集流器轴向间隙对多翼离心风机性能影响的示意图如图11所示。由图11可知:当轴向间隙过小时,气流进入叶轮后无法快速地由轴向转变为径向流动,使叶轮前端形成低速漩涡流动,叶轮的做功能力下降;适当增加轴向间隙时,虽然集流器与叶轮间泄露流量会略有增加,但进入叶轮的气流可以更好地完成速度方向的转变,提高叶轮前端做功能力,使风机整体性能提高;当进一步增加轴向间隙时,对叶轮前端做功能力的提升效果已经不明显,但却会增加集流器与叶轮之间的泄露流量。当增加的泄露流量超过叶轮前端做功能力提升带来的流量增量,就会使风机的气动性能下降。

3 内部流动分析

由数值模拟结果得出,在所研究的模型中,当集流器参数δ=6 mm、do=206 mm时,风机具有最优的气动性能,其性能参数与原风机性能参数对比如表3所示。由表3可知:最佳设计的风机在最大风量设计点,风机的风量相比原型风机增加了1.62 m3/min,全压相比原型风机增加了23.69 Pa,但容积效率相比原型风机下降了1.76%;在效率最高点,风机的风量较原型风机增加了0.42 m3/min,内效率较原型增加了1.31%。

表3 原型风机与优化风机数值模拟结果对比

图12为多翼离心风机内部流动的观察平面,图中平面1为非电机侧叶轮50%叶高处所在平面,平面2通过风机旋转中心。

图12 内部流动观察平面位置示意图

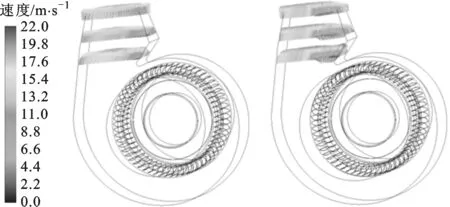
优化设计的风机与原型风机在平面1上的速度云图如图13所示。由图13可知,经过优化设计的风机在叶轮出口区域的速度增加。在靠近蜗舌的出口区域,原型风机内有较为明显的低速区,这种流体滞留现象使得风机出口的实际通流面积减小,从而影响到风机的流量。优化设计的风机出口的低速区基本消失,出口速度较原型风机更为均匀。

(a)优化风机 (b)原型风机图13 平面1速度云图

图14所示为优化设计的风机和原型风机出口区域的速度矢量图。由图14可知,在风机出口不同截面位置处,原型风机在靠近蜗舌处有回流,而优化设计的风机在相同位置处的回流明显减少,且优化设计的风机在出口区域的速度分布较原型风机更为均匀。由于风机流量取决于出口区域的流体速度与流道截面积,因此在风机流道保持不变的情况下,优化设计的风机的流量和全压都得到了提升。

(a)优化风机 (b)原型风机图14 风机出口截面速度矢量分布

优化设计的风机与原型风机在平面2上的速度分布如图15所示。由图15可知:优化风机在叶轮右侧前端的速度得到了提升,减小了前端气体的湍流,增加了叶轮做功能力,从而使得风机的效率得到提升;但与此同时,由于轴向间隙的增大和出口直径的减小,风机中由蜗壳经集流器与叶轮间环状间隙泄露的流量也较原型有所增加,风机的容积效率下降。

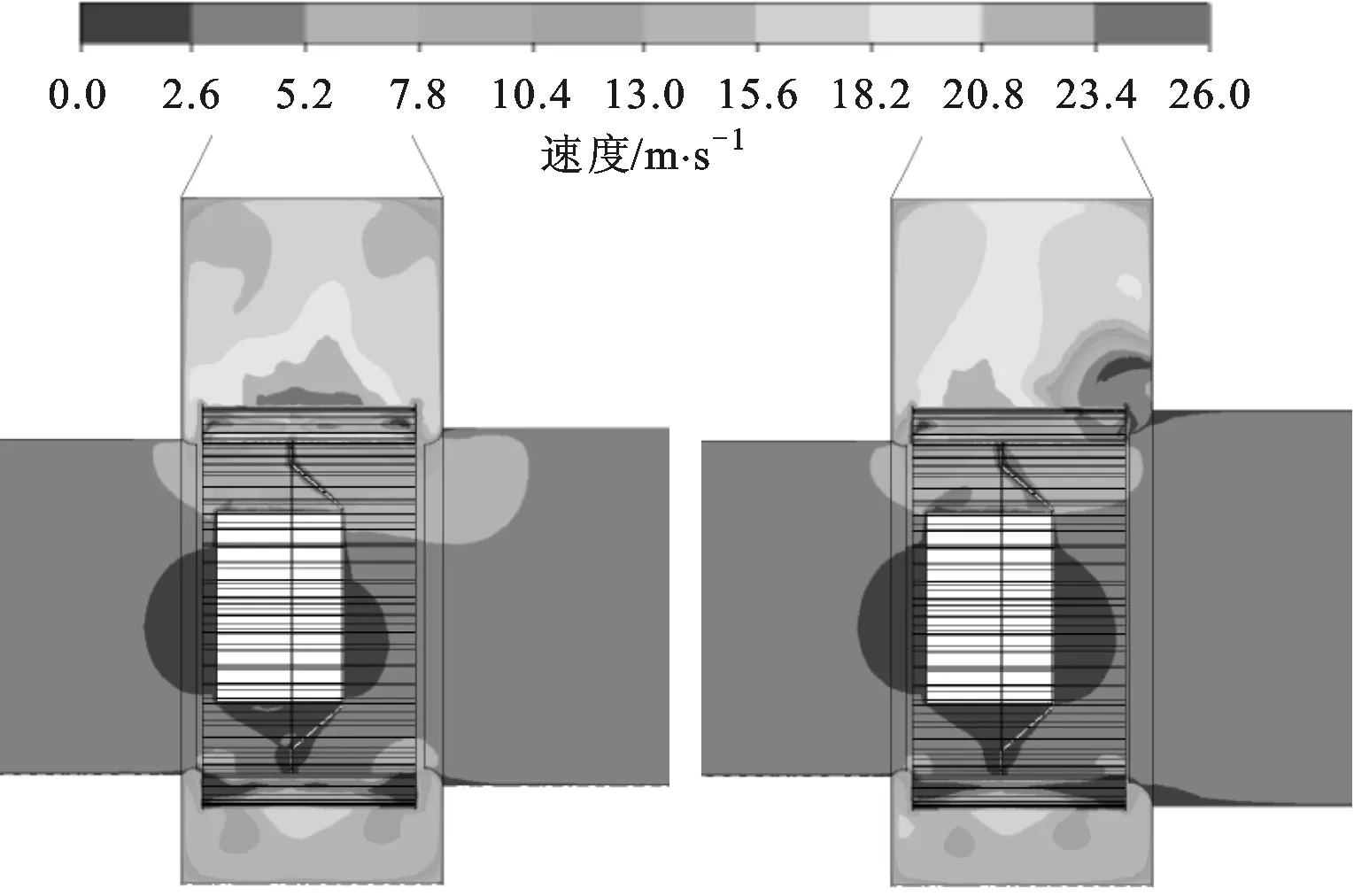
(a)优化风机 (b)原型风机图15 平面2速度云图

4 实验验证

将轴向间隙δ=6 mm、出口直径do=206 mm的集流器进行加工打样,然后与原型集流器分别装到同一台风机上进行测试,优化设计风机和原型风机的气动性能曲线如图16所示。由图16可知,采用优化的集流器,风机最大流量增加约1.0 m3/min,风机的静压值在全工况范围内均有提升,最大静压提升约25 Pa。

图16 优化设计风机与原型风机的性能曲线

5 结 论

针对吸油烟机用多翼离心风机,本文采用数值方法研究了集流器轴向间隙和出口直径对风机气动性能的影响,并对典型工况点进行了性能测试和验证,得到如下主要结论。

(1)本文建立的吸油烟机用多翼离心风机数值计算模型及方法,能够有效模拟多翼离心风机气动性能,内部流动结构的分析可以作为多翼离心风机性能改进的依据。

(2)集流器轴向间隙和出口直径对风机性能均有影响,其中出口直径对风机性能的影响比轴向间隙更大,但从设计的角度来说,对于多翼离心风机存在一个最佳的轴向间隙与出口直径比值;风机进口位置处集流器结构参数的变化不仅影响到风机进口区域的流动,还会对风机叶轮内流动及出口区域的流动产生较大影响。

(3)采用参数优化集流器,可以有效改善风机出口流动状态。数值模拟结果表明:优化设计的风机的最大流量增加了1.62 m3/min,压力增加了23.69 Pa,而容积效率下降了1.76%;在最高效率点,风机风量较原型风机风量增加了0.42 m3/min,风机内效率增加了1.31%。实验结果验证了风机的气动性能在全工况范围内都得到了提升。