差异性随机子空间集成*

丁 毅，王明亮，张道强

南京航空航天大学 计算机科学与技术学院，南京 211100

1 引言

集成学习是机器学习中的一个重要研究领域，在很多的实际问题研究中，集成学习往往能比单一的机器学习算法获得更好的效果。构建一个集成算法主要分为模型构建和模型组合两个步骤[1]，而构建一个好的集成算法的关键在于基学习器的性能和差异性，但大多数实际情况下很难同时实现这两个目标[2]。目前已经有很多关于提高基学习器之间差异性的研究工作[3-4]。构建具有差异性的基学习器的4种基本方法有：（1）使用不同的组合模式；（2）使用不同的学习器；（3）使用不同的特征子集；（4）使用不同的训练集。在目前的研究中，第三种和第四种集成算法构建方法更为常见，第三种最具代表性的就是随机子空间集成（random subspace ensemble，RSE）[5]，它通过大量随机选取特征子空间来分别构建基学习器。而在第四种方法中，又分为直接随机选取训练子集和自适应调整训练集的方法，最具代表性的即Bagging[6]和Boosting算法中的Adaboost[7]。另一种常用的集成学习算法：随机森林（random forest，RF），同时具备第三种和第四种集成算法构建方式的特征，不仅每次随机选取训练集，并且每次在构建决策树的时候随机选择特征作为结点。在很多实际应用中，集成学习算法能获得很好的性能，而选择哪种具体的算法则要根据实际的情况来确定。Boosting类型算法，例如Adaboost[7]，在噪声较少的数据集上能获得更优秀的性能，却容易过拟合有噪声的数据集[8-10]，而Bagging和RSE则表现得更加鲁棒[11]，尤其当数据具有很高的维度-数量比和很多冗余特征的时候，RSE能获得更好的性能。

在很多实际应用中，例如功能磁共振影像（functional magnetic resonance imaging，fMRI）分类任务中，医学数据的样本量较少，而fMRI数据的维度又非常高，文献[12-14]都利用RSE成功地在这个任务上获得了很好的性能。但是当给定一组基学习器时，选择使用其中的一部分要比直接使用所有的基学习器要更好，因此如何选出这样一组基学习器对于集成学习来说非常重要[15]。在集成学习中，基学习器之间的差异性是集成方法性能的关键，从所有的基学习器中选择出一组最具差异性的不仅可以帮助减少基学习器之间的冗余度，而且可以提高集成方法的性能。目前已经有很多关于基学习器之间差异性的研究，如文献[16]的Chapter 5，但是这些方法并没有真正考虑到随机子空间集成的特性，即随机子空间集成的差异性应该体现在子空间分布结构的差异上。因此本文基于聚类的思想，利用多核最大均值差异（maximum mean discrepancy，MMD）来衡量子空间的分布差异，提出了一种无监督和不需要训练的差异性随机子空间选择算法，并利用选择到的差异性随机子空间得到差异性优化的集成模型。

2 随机子空间集成

2.1 符号解释

给定数据集X=[x1,x2,…,xN]∈RD×N，和对应的标签Y=[y1,y2,…,yN]∈R1×N，随机采样的第i个d维子空间数据集为一个集成学习模型由M个基学习器组成f(x)={f1(x),f2(x),…,fM(x)}，其中fi(x)表示为一个基学习器。

2.2 随机子空间集成

给定数据集X，随机选取M个d维子空间，从而得到M个新数据集。基学习器fi(x)可以根据学习任务的需要进行选择，例如支持向量机（support vector machine，SVM）、逻辑斯提回归（logistic regression，LR）、最小二乘回归（least square regression，LSR）、决策树（decision tree，DT）等。一个基学习器对一个子空间数据集进行学习，最终综合所有M个基学习器的结果输出结果。当每个基学习器给出预测结果后，可以选择多种方式来集成所有基学习器的结果。最常用的包括取均值、加权平均值、投票等方式[16]。

2.3 集成剪枝

集成剪枝是提高随机子空间集成算法的推广能力和效率的有效方式。集成剪枝主要分为3种类型[17]：（1）基于排序的剪枝；（2）基于聚类的剪枝；（3）基于优化的剪枝。基于排序的剪枝[18]即给定所有的基学习器一个合适的顺序。基于聚类的剪枝技术[19]基于利用基学习器的特性进行聚类，采用某种合适的策略从一个聚类中选取一个模型加入集成中。而基于优化的剪枝[15]则是通过给每个基学习器一个权值，通过优化一个设计的目标函数来学习到这个权值。然而这3种剪枝方法的前提都是先训练好所有的基学习器，这需要大量的计算资源，并且对于RSE来说，这些策略并没有充分地提高随机子空间的差异性。

3 差异性随机子空间集成

3.1 子空间差异性度量

子空间的差异性来源于样本在这个子空间中的分布情况，如图1所示，有4个不同分布结构的二维子空间，不同的子空间分布结构代表着不同的信息，需要尽可能利用不同的子空间信息，并且删去大量的冗余子空间，例如在图1中的第一个和第四个子空间具有非常相似的空间结构，基于这两个子空间的基学习器不能够相互提供足够的互补信息，因此只需要利用这两个子空间中的一个。为了达到这个目的，需要找到一种合适的度量来衡量子空间之间的差异性，从而选取最具有差异性的子空间加入集成中。

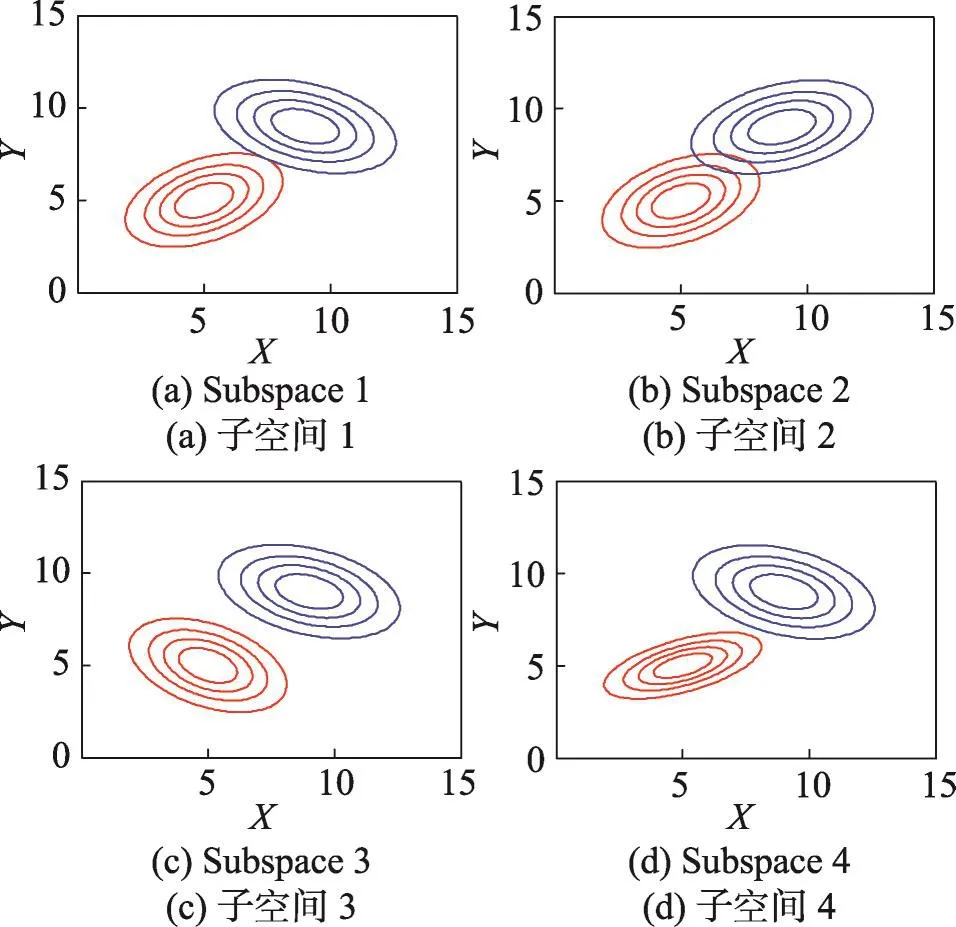
Fig.1 Subspaces with different distribution structures图1 具有不同分布结构的二维子空间

衡量数据的分布差异一般通过数据的一阶、二阶统计信息即均值、方差来衡量，而低阶的统计信息不足以完全表达出数据分布的信息。最大均值差异（MMD）[20]是一种非参数度量，最开始被使用在验证两组样本是否属于同一数据分布，它通过将数据分布投影到再生核希尔伯特空间（reproducing kernel Hibert space，RKHS）来计算它们之间均值（即高阶统计量）的差距。MMD的公式化描述如下。

定义1令ϕ:X→H是从特征空间到RKHS的投影，X、Y表示两个数据集，两个数据集之间的MMD定义为：

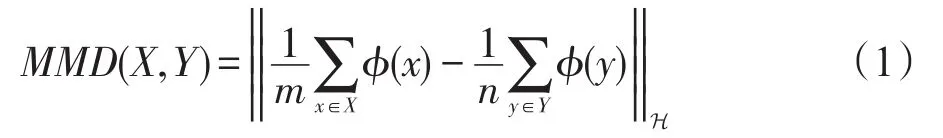
当S1和S2属于同一数据分布时，MMD值为0。当选取合适的核函数k，式（1）可以被进一步展开为：

计算式（2）即计算两个子空间之间的MMD的时间复杂度，为O(n2)，在本文的任务中n为数据集的样本量，而计算所有子空间之间的MMD的时间复杂度为O(n2m2)，其中m为随机选取的子空间的数量。在实际应用中，数据量n往往会大于子空间数量m，此时计算开销将主要消耗在计算MMD上。在这里使用多核MMD（multi-kernel MMD，MK-MMD）[21]来进行线性的MMD计算，从而极大降低复杂度。将式（2）中的核函数k替换为多核核函数：

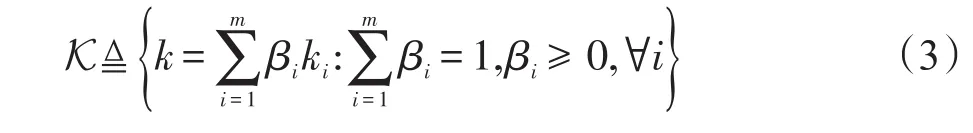
根据文献[21]中的理论分析，核函数的选择对于双样本问题的检验能力十分重要，这里的多核通过利用不同的核函数来强化MK-MMD的检验能力。类似于文献[21]，采用式（2）的无偏估计来表示MKMMD，这种表示可以被在线性时间内完成计算。选取样本元组vi:=[x2i-1,x2i,y2i-1,y2i]，

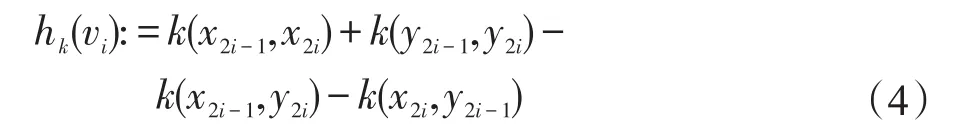
此时两个子空间的MMD表示为：

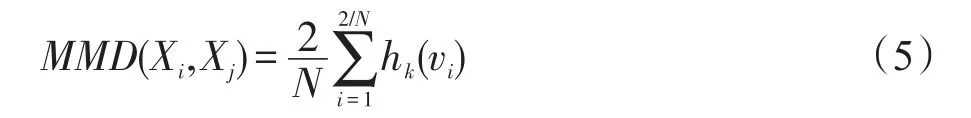
从而，可以利用式（5）来衡量两个子空间中数据分布的差异性。并且计算式（5）的时间复杂度降低到O(n)。下一步，需要选取合适的多核参数β来最大化MK-MMD的能力同时最小化TypeⅡError[21]，目标函数定义为：

从而式（6）被表示为：

其中，λ=10-4。通过求解式（7）这个二次规划问题，得到优化的多核参数β来计算MK-MMD。

3.2 基于聚类的差异性随机子空间选择

本文利用聚类的思想，利用MK-MMD作为距离度量，通过将具有相似数据分布的子空间聚到同一类中，选取这个聚类里的一个子空间作为代表，从而减少随机子空间的冗余度。常用的聚类方法有K均值算法（K-means）、均值漂移（mean shifit）、谱聚类（spectral clustering）和高斯混合模型（Gaussian mixture）等。而在本文仅仅有子空间之间的距离信息，这使得需要计算聚类中心的聚类算法无法使用，因此在这里采用基于图的谱聚类算法结合基于MKMMD的相似性度量来进行随机子空间之间的聚类。谱聚类首先利用数据样本构造相似性矩阵。然后利用相似性矩阵得到拉普拉斯矩阵（Laplacian matrix），通过拉普拉斯矩阵的特征向量构造一个新的、简化的数据空间，在这个数据空间中数据间的相似性关系表现得更加直观。最后得到随机子空间的聚类结果后，从每个聚类中选取一个最具代表性的随机子空间来代表这个聚类。在本文中，利用聚类C中的一个子空间i对于其他子空间的相似度的和作为其重要程度，如式（6），选择重要程度最高的子空间作为聚类C的代表，并加入差异性随机子空间（diverse random subspace，DRS）中：

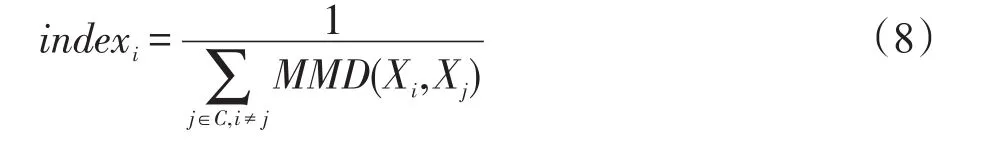
差异性随机子空间选择的算法如算法1所示。

算法1差异性子空间选择

输入：随机子空间集合RS∈RM×N×d（其中M为子空间数量，N为样本数量，d为子空间维度），子空间聚类数量n。

（1）构建子空间相似性矩阵A∈RM×M：

①对于任意两个随机子空间RSi和RSj，利用式（5）计算它们之间数据分布差异MMDi,j；

②当RSi和RSj分布一致，则MMDi,j=0，RSi和RSj的相似性定义为1/MMDi,j；

③Ai,j=1/MMDi,j。

（3）对拉普拉斯矩阵L进行特征分解，将其中前k个最大特征值所对应的特征向量v1,v2,…,vk组合成新矩阵V=[v1,v2,…,vk]∈RM×k，并对矩阵V按元素进行归一化。

（4）V中的第i行可以看作是第i个子空间的一种特征表示，对V中的样本使用k-means算法聚类。

（5）在第i个聚类Ci中，根据式（8）计算每个随机子空间的重要程度，选择重要程度最高的子空间作为聚类Ci的代表，并加入到最后的差异性子空间集合DRS中。

输出：差异性子空间DRS∈Rn×N×d。

3.3 差异性随机子空间集成

当得到一组差异性子空间集合DRS后，可以利用多种基学习器进行学习，例如决策树、逻辑斯提回归等。本文使用逻辑斯提回归（LR）作为基学习器作为默认的DRS算法。LR是被广泛应用的分类模型，LR有着较为稳定的分类性能，并且相比于同样受到广泛关注的支持向量机，LR更加容易训练（在大规模应用中可以利用随机梯度下降等优化方法），并且更容易实施（SVM需要存储大量的支持向量，而LR只需要计算一次向量的内积）。基于DRS的集成学习算法在训练之前即进行了大量的剪枝，并且能够保证剩余的随机子空间保留足够的差异性。虽然保证基学习器的差异性是被广泛接受的集成算法设计思想[16]，但是在大多数情况下仍然无法保证基于差异性的基学习器能够获得优秀的性能并且组成一个高性能的集成学习算法。由于DRS通过优化差异性显著降低了基学习器的数量，因此在本文中，将DRS和基于排序的集成剪枝技术结合。首先，将在验证集上性能较差的，例如将分类精度低于50%的基学习器直接丢弃，然后根据训练好的基学习器在验证集上的表现进行排序，选取前k个基学习器作为最终的集成模型。差异性随机子空间集成算法如算法2所示。

算法2差异性子空间集成

输入：差异性随机子空间DRS∈Rn×N×d，基学习器f(x)，验证集V，测试集T，基学习器参数σ，集成大小k(k≤n)。

（1）使用基学习器f(x)和对应的参数σ对DRS集合中的每一个随机子空间进行学习。

（2）每个基学习器f(x)对验证集V进行验证得到验证结果Vri=f(DSRi)。

（3）过滤Vri≤0.5的基学习器。

（4）根据Vri对基学习器进行排名，选取前k个基学习器加入集成E。

（5）使用最终的集成E对测试集T进行测试。

输出：训练后的差异性随机子空间学习器集合。

4 实验与分析

4.1 模拟数据集

构造一个模拟数据集来验证差异性随机子空间选择算法的效果。

首先构造一个具有明显判别性分布的二维数据集。分别从两个二维高斯分布中各随机采样200个数据点，得到原始数据集A。原始数据分布如图2所示。

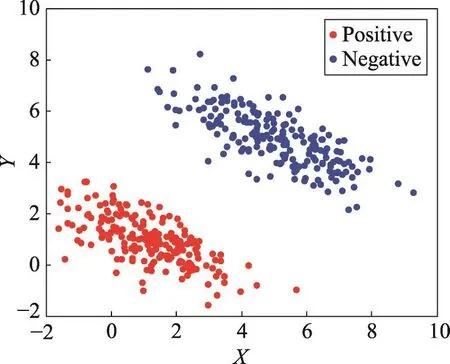
Fig.2 Original feature space图2 原始特征空间

为了验证差异性随机子空间集成的效果，为原始具有判别分布特性的两个维度加入8维高斯白噪声来混淆原始数据，得到新的数据集B。对数据集B随机采样100个二维随机子空间，经过分析，总共有45种不同的二维随机子空间，其中具有差异性的随机子空间只有4种，即原始的两个维度，原始的其中一个维度加上噪声维度和全噪声维度。希望从随机采样的100个二维随机子空间中利用本文提出的差异性随机子空间选择算法找到这4种差异性随机子空间。

在算法执行后，从100个二维随机子空间中得到了4个随机子空间聚类，通过式（6）定义的准则，从每个聚类中选取一个随机子空间作为该聚类的代表，随后得到了图3中的结果，图3中明确给出了通过算法1得出的4个差异性随机子空间的分布结构。通过分析，可以明确看到算法1所选择出来的差异性子空间确实是这100个二维随机子空间所具备的4种基本分布结构，实验结果表明了本文提出的差异性随机子空间选择的算法有理论上的作用。在4个聚类中，第一个聚类中只有图3中的第一个差异性子空间，第二个聚类中只有图3中的第二个差异性子空间，第三个聚类中有16个随机子空间，如图4所示，第四个聚类中有82个随机子空间。以图4为例，第三个聚类中大多数和图3中的第三个子空间有相同的分布，只有少部分的错误聚类，可以观察到第三个聚类中出现了第二个聚类中的子空间，这是因为所构建的差异性随机子空间选择算法中的谱聚类过程受到了相似性矩阵尺度化的影响和图分割算法的影响，这导致只能够得到差异性随机子空间聚类的近似最优解，但是最终的代表性子空间选择算法（算法1，步骤5）可以帮助排除小部分错误聚类的影响。

4.2 真实数据集

本文也比较了差异性随机子空间集成（DRS）、随机森林（RF）、随机子空间集成（RSE）、Adaboost、Bagging和支持向量机（SVM)等算法在真实数据集上的性能。选用了10个公开数据集（https://www.csie.ntu.edu.tw/～cjlin/libsvmtools/datasets/，http://adni.loni.usc.edu/，http://archive.ics.uci.edu/ml/）。其中 MCI数据集来自于 ADNI（the Alzheimer's disease neuroimaging initiative）数据集，ADNI数据集是一个公开的用于研究老年痴呆症（the Alzheimer's disease）的数据集，包含了MRI、PET等多种模态的数据，利用MCI（mild cognitive impairment，轻度认知障碍）的数据和正常人进行分类，由于MCI是老年痴呆症的前兆，因此选择这个任务也具有很大的意义。通过MRI数据构建脑网络[22]来提取4 005维特征进行分类，而另外9个常用公开数据集则来自于UCI数据集库和Libsvm数据集库。其中有4个数据集具有很高的特征-样本比，另外3个数据集则是普通的数据集。在这里子空间中都利用LR作为基学习器。希望通过使用这7个数据集来了解基于差异性随机子空间集成的方法的优劣性。在本文的所有实验中，使用5折交叉验证的方法分割训练集和测试集，总共进行20次5折交叉验证的过程。DRS、RSE随机采样一半原始维度的子空间200次，DRS聚类后得到50个差异性子空间。其中RF、Adaboost、Bagging的基学习器数量被限制在200个。

Fig.3 Diverse random subspace图3 差异性随机子空间

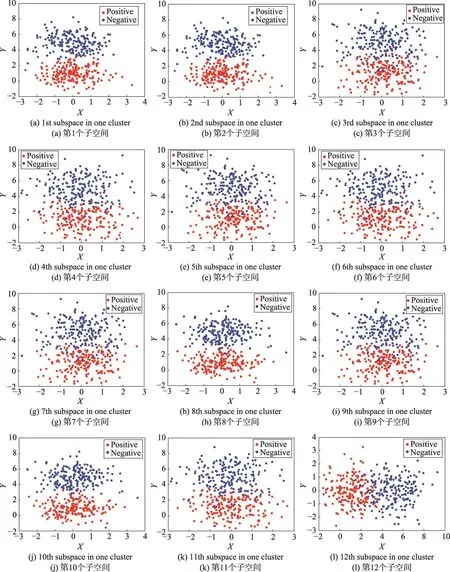
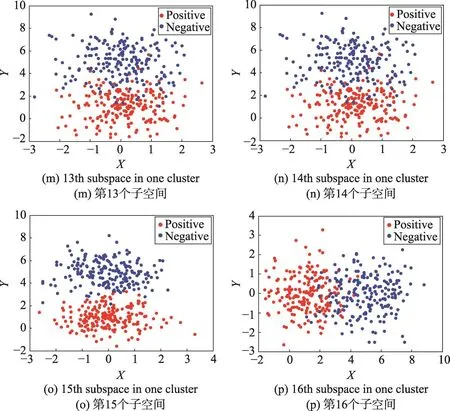
Fig.4 The third cluster of subspaces图4 第三个随机子空间聚类中的子空间

表1、表2中展示了所有的实验结果，其中ratio表示数据集的特征-样本比。由表1、表2中可以看出，在特征-样本比较高的数据集上，由于存在大量的冗余特征，因此降低了特征维度的随机子空间和本文提出的差异性随机子空间的方法能获得很高的效果。在其中几个数据集上，只有20个基学习器的差异性子空间集成方法超过了有200个基学习器的RF、Adaboost、Bagging算法，而相比较于有众多基学习器的随机子空间方法RSE，差异性子空间集成由于极大削减了由冗余噪声组成的众多噪声子空间，在大部分数据集上得到了超越RSE的结果，并且在训练和测试上有更高的效率。但是对于低维度的数据集，基于随机子空间的RSE和DRS算法的基学习器失去了很多的关键信息，导致基学习器的性能都很差，集成的结果也无法提高。当数据集中存在大量的冗余特征时，差异性随机子空间算法是提高常用的随机子空间方法RSE的一种有效途径。值得注意的是，和谱聚类等其他聚类算法一样，RSE中聚类的数量的选择作为一种超参数不具备单调的对性能的影响，因此在实际应用中，可以利用交叉验证的方法选择出合适的聚类数量来提高最终性能。

Table 1 Comparison between different methods（High feature-sample ratio）表1 不同集成方法之间的比较（高特征-样本比）

Table 2 Comparison between different methods（Low feature-sample ratio）表2 不同集成方法之间的比较（低特征-样本比）

5 结束语

很多的真实数据集有很高的特征维度并且缺少足够的样本来训练单个学习器，在这些高维特征中也存在着许多冗余的特征，这些特征会导致很多常用分类器的失效。在这种应用场景下，随机子空间集成方法由于对子空间进行了频繁的采样，从而在减少了冗余特征的随机子空间中构建性能更好的基学习器，对基分类器集成后得到更强大的集成算法。在很多情况下，冗余特征甚至会超过有效特征，从而采样得到的大部分随机子空间可能具有相同的数据分布，减弱了基学习器之间的差异性。本文提出了一种基于数据分布的差异性随机子空间集成方法，利用MK-MMD在线性时间内计算子空间之间的分布差异，并通过谱聚类的方法将相似的子空间集合到一起，并利用一定的准则选出一个代表性子空间，得到差异性的随机子空间集合。实际的实验表明，在大多数情况下，差异性随机子空间集成的方法要强于随机子空间集成，而在低维度数据集上，差异性随机子空间集成和随机子空间集成的性能都远差于随机森林、Adaboost、Bagging方法，这说明在不存在冗余特征的条件下，子空间无法充分利用有效信息，从而降低了集成方法的能力。本文提出的差异性随机子空间集成方法是提升随机子空间集成的一种直接而有效的途径，未来差异性随机子空间选择方法可以进一步扩展到随机森林、特征选择等方面。