基于数形结合的乘法分配律错例分析
2018-09-11安徽马鞍山市四村小学教育集团243000
安徽马鞍山市四村小学教育集团(243000)
教材四年级下册“运算定律”这一单元,总能听到很多教师抱怨:“学生怎么就找不到乘法分配律中的公因数呢?”“三个数、四个数连乘,肯定是用乘法交换律或是结合律,这些孩子怎么会用上乘法分配律呢?”“学完整个单元后,学生出现的错误简直五花八门,一片混乱。”……
除了五条基本运算定律外,连减、连除的简便计算以及加减、乘除的灵活应用等相关内容也被编排在“运算定律”这一单元。整个单元知识点系统全面,但对于四年级的学生来说,却具有一定难度,其中的乘法分配律似乎成了学生很难跨越的“坎”。

运算定律 运算性_质___________________________________________名称___加法_______________________交换律___加法__________________结合律___乘法_______________________交换律乘法结合律____________乘法分配律_____________减法的运算性质字母表达式____________a+b=b+a_____________(a+b)+c=a+(b+c)________a×b=b×a_____________(a×b)×c=a×(b×c)_________(a+b)×c=a×c+b×c__________a-b-c=a-(b+c)除法的运算性质a÷b÷c=a÷(b×c)(b≠0 ,c≠0)
从上表可以看出,与其他只包含单一运算的运算定律和性质相比,乘法分配律含有乘法与加法两种运算,思维含量较高。同时,乘法分配律与乘法结合律在形式上最为相似,也给学生造成一定的干扰。如果只重视乘法分配律外在形式的识记与模仿,忽略对其本质意义的理解,学生自然会出现(a×b)×c=(a+b)×c、(a+b)×c=a×c+b之类的错误。
当学生出现错误时,如果能结合具体的情境,将直观的形与抽象的数一一对应,将有助于学生深刻理解乘法分配律的内在本质,从而有效建构抽象的运算律。
【错例一】(提取练习)38×36+64×38

图1
分析:从乘法分配律的字母表达式来看,其应用是双向的。从左往右看,从(a+b)×c到a×c+b×c是分解式思维;从右往左看,a×c+b×c到(a+b)×c是提取式思维。“从左往右”的应用符合学生的认知习惯,“从右往左”则让一些学生如同雾里看花。
对策:
师(出示:401班为38名女生统一购买表演服装,其中上衣36元,裙子64元,一共花了多少钱?):你能列出算式吗?
生1:38×36+38×64,38×36表示38件上衣的总价,64×38表示38条裙子的总价,再把它们加起来,就是一共花的钱数。
生2:我觉得这样计算比较麻烦。上衣和裙子都要买38件,可以先算“一套衣服的价格”,再乘38。列式为(36+64)×38。
师:这是生活中常见的购物问题,虽然两个算式“长”得不一样,但都能解决这个数学问题。
生3:38×36+38×64=(36+64)×38,这就是运用了乘法分配律。
师:用不同颜色的笔在图(如图2)上圈一圈,表示这两种算法。
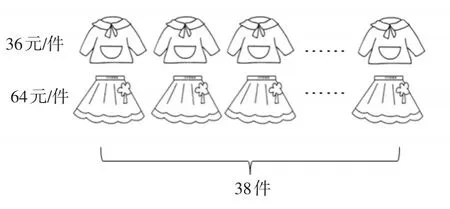
图2
生4:虚线框表示分别算出上衣和裙子的总价,再相加。实线框表示先把每套衣服算出来,36+64正好等于100元,一共38套,再用100乘38就行了,计算很方便。
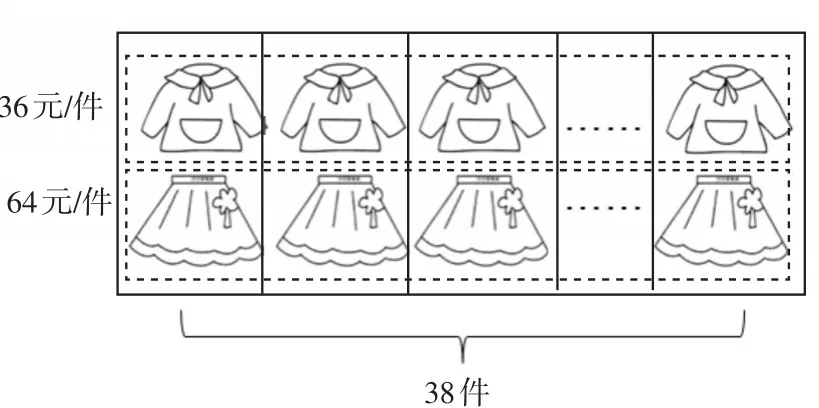
图3
师(出示图1):有位同学计算38×36+64×38时遇上了麻烦,虽然也想到了乘法分配律,却越做越觉得不对劲。你有什么看法?
生5:我觉得36和38很接近,他是不是搞不清哪个才是公因数?
生6:这可以和刚才的买衣服问题联系起来,只不过64和38调换了位置,相当于运用了乘法交换律。
生7:我建议在观察算式后,把38圈起来,这样就不会错了。
生8:38×36可以理解为36个38,64×38可以理解为64个38,这样一共是(36+64)=100个38,怎么可能是102个36呢?
【错例二】(对比练习)25×44
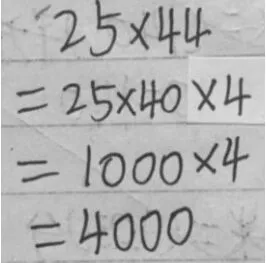
图4
分析:简便计算本身就是一个开放的思维过程。25×44,既可以把44拆成40和4的和,运用乘法分配律,也可以把44看作4和11的积,运用乘法结合律。正因为方法的不唯一,有些学生就会张冠李戴、混淆不清。
对策:
师(出示图4):这样计算对吗?
生1:44应该是40和4相加,不是相乘。
生2:如果将两个数相乘,变成三个数连乘,应该把44看成4和11相乘,见25“想”4,25×4的积再乘11,结果应该是1100。
生3:这是把乘法分配律和乘法结合律混在一起了。
师(出示:在广场表演中,有44支队伍,每支队伍25人,一共有多少人?):这道题可以列式为“25×44”吗?
生4:列式正确。“一共有多少人”就是求44个25是多少,所以用乘法计算。
师:在三年级学习“两位数乘两位数”时,我们借助点子图来理解算理。今天计算“25×44”,我们也在点子图上圈一圈、分一分,感受不同的算法。
学生独立完成,展示:
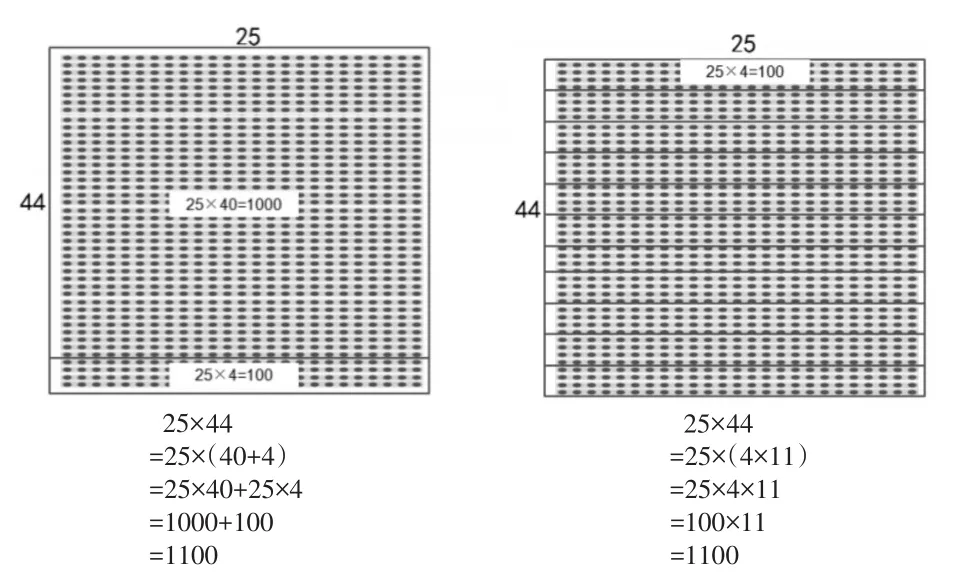
图5
师:对比图5中的两种算法,你有什么发现?
生5:如果想把44分成40和4两部分,那只能运用乘法分配律,25要和40相乘,也要和4相乘,最后把两个积相加。
生6:25和4相乘是100,44里面有11个4,所以这实际上是乘法结合律,本来是4先和11相乘,现在是25先和4相乘,然后再乘11。
生7:这两种方法都很方便,就看是想拆成和还是积。
生8:25×44=25×40+25×4,其实就是44个25等于40个25加上4个25,25×44=25×4×11,表示44个25等于11个25×4。
【错例三】(变式练习)99×99

图6
分析:一些本身不具备乘法分配律特征的习题,通过变式,可以还原成基本模型题。大多数学生简算99×99时会想到99×(100-1),个别学生反而“想多了”,变式为(100-1)×(100-1),说明这些学生并没有将乘法分配律的本质纳入自身的知识结构中。
对策:
师:看到99×99,能让你联想到我们学过的平面图形吗?
生1:我想到正方形,正方形的面积就是“边长×边长”。
师:想象一个边长是99米的正方形果园,果园的面积就是99×99。怎样计算呢?
生2:99×99表示99个99,可以用100个99减去1个99,也就是99×100-99。
师(出示图7):想象一下,这个果园的一条边长增加1米,就是100米。现在果园是什么形状的?增加的部分又是什么形状呢?
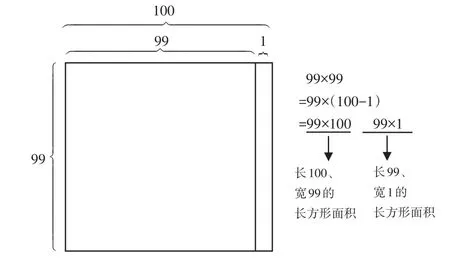
图7
生3:现在的果园是一个长100米、宽99米的长方形,增加部分也是一个长方形,长99米、宽1米。
师:99×99=99×100-99×1,谁能结合图7说说每一步的含义?
生4:99×99是原来正方形的面积,99×100-99×1是增加后的长方形面积减去增加的长方形面积。
师:从乘法的意义和面积图的含义两方面来看,这种算法能说得通。
师(出示图6):有位同学想到99接近100,所以他把99×99转化成(100-1)×(100-1),这样行吗?
生5:不行。乘法分配律不论是两个数相加的和还是两个数相减的差,都要乘一个相同的数。他这样做,括号里都是两个数的差,变成了四个数,这怎么乘呢?
师:如果觉得不好理解,试着发挥你们的联想功能。把正方形果园的边长从99米增加到100米,变成一个更大的正方形。那100×100、100×2分别表示什么?
生6:100×100表示增加后的正方形面积,100×2其实是两个长100米、宽1米的长方形面积之和。
师:看上去似乎也能说得通,是不是还有什么被我们忽略了?
生6:我知道他出错的原因了。这两个长100米、宽1米的长方形里,重叠了一个边长是1米的小正方形。如果从100×100里减去2个100×1的话,等于减去了2次小正方形面积,所以还要加上1×1。
师(出示图8):从算式的角度观察只知其错,和图形结合起来,我们才能知其错因。
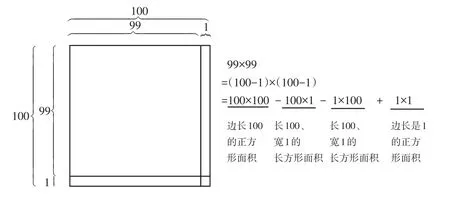
图8
反思:
对于学生来说,运算定律的提炼与概括具有高度的抽象性。但学生不是一张白纸,他们在学习乘法分配律之前已经积累了大量的知识与活动经验,如学习乘法口诀(如图9-1)、长方形周长的计算方法(如图9-2)、两位数乘两位数的笔算方法(如图9-3)时,都在不知不觉中运用了乘法分配律。教师要引导学生用好这些经验,完成知识学习的迁移过程,从而帮助学生将原来零散的感性认识上升到理性认识,让学生能够在回忆中逐步建立数形模型。
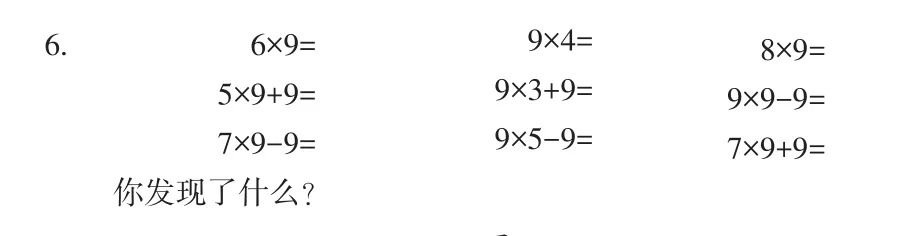
图9-1
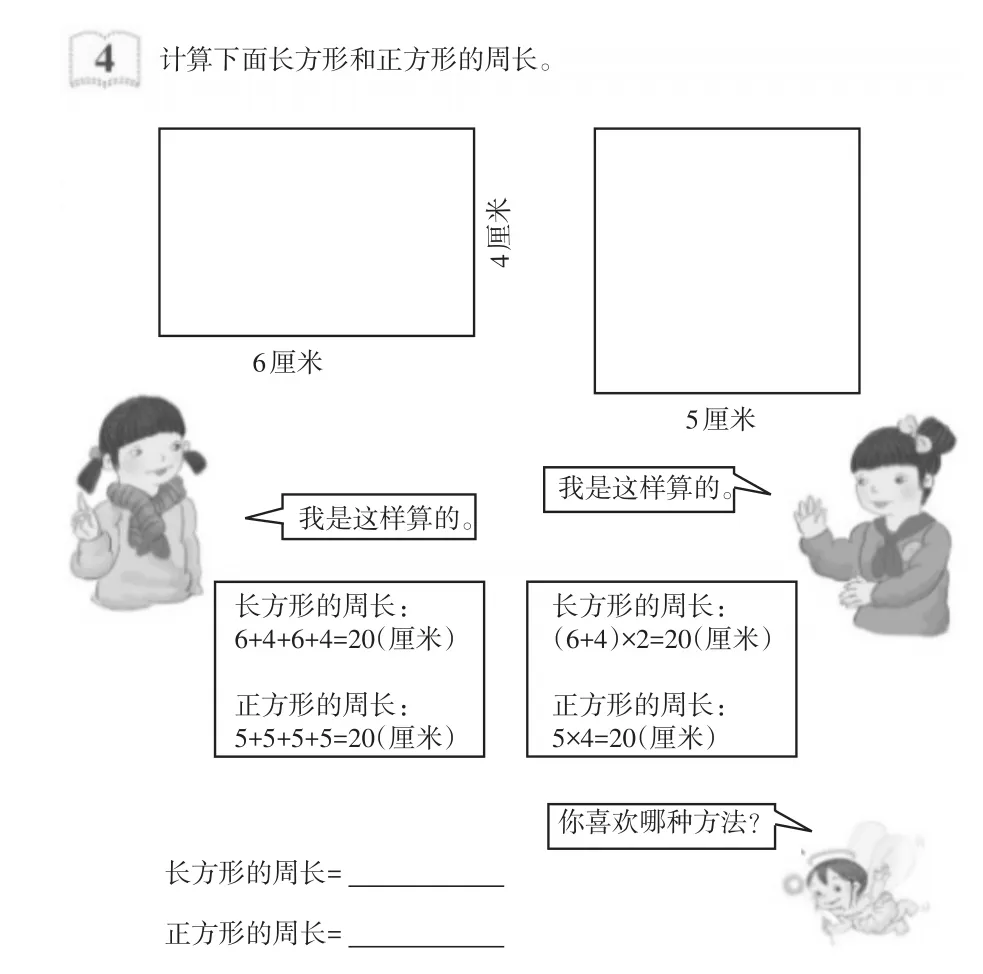
图9-2
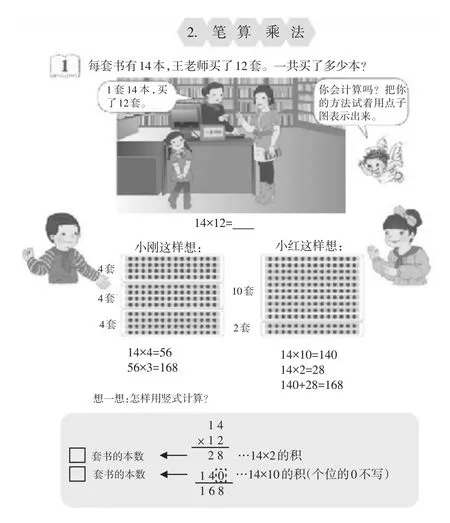
图9-3
学生出错在所难免,但即使出现错误,也要错得明明白白。教师要在生活中寻找与运算定律相关的素材,从图形出发,以图形为载体,注重数形结合,在数形中加深学生对意义的理解,多维度促进学生对乘法分配律意义的建构,从而帮助学生理解并灵活应用运算定律。
