谈苏教版教材中的“解决问题的策略”
2018-09-11江苏太仓市科教新城南郊小学215400
江苏太仓市科教新城南郊小学(215400)
“解决问题的策略”是苏教版教材独有的,体现了苏教版教材的“人无我有,人有我强,人强我优”的思想,是教材的一大亮点。这个内容的设置能更好地落实新课标的理念,提高学生的解决问题的能力。
一、现状分析
1.多种策略,顺应儿童学
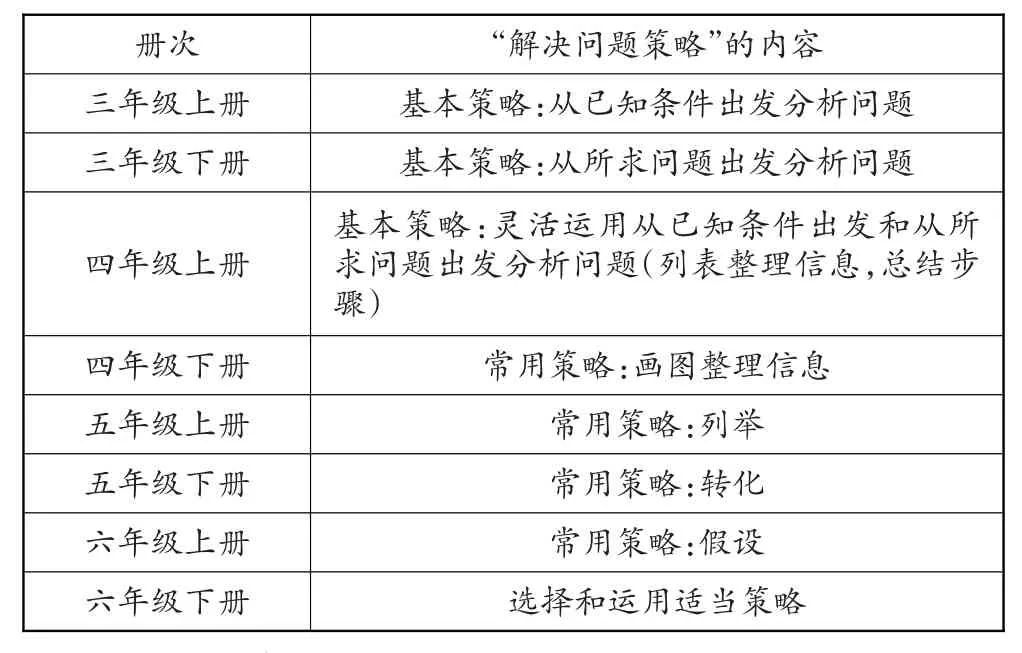
解决问题的策略不但是苏教版教材独有的,修订版的教材在三年级上册和三年级下册又增加了“从已知条件出发分析问题的策略”和“从所求问题出发分析问题的策略”,使策略更完整,更有利于学生分析问题和解决问题。修订版教材在三到六年级的每一册都安排了与策略相关的内容:
?
从上表可以看出,苏教版的教材不但有基本策略,也有常用策略,在六年级下册还对策略有一个应用和回顾:从已知条件出发分析问题和从所求问题出发分析问题给了学生解决问题的基本思路;画图和列表的策略能化抽象为具体形象,符合学生的认知特点;列举的策略能发展学生的数学思考能力,因为列举要做到不重复不遗漏;转化的策略在后续的学习中有着举足轻重的作用,如小数除法转化成整数乘法,面积公式的推导都是先转化成旧知;假设法则是为初中服务的,是代数思想的开端。这些策略的学习有利于提高学生解决问题的能力和数学思维能力,帮助学生积累数学活动经验,发展学生的创新意识。
2.直接呈现,为策略而策略
教材在呈现某些“策略”时存在着一些问题,只是为了策略而策略,让人感受不到策略的有用性,具体为什么要运这个策略学生说不上,自然不能促进学生将其转化为内在的需要。
如五年级上册“一一列举的策略”的例1:王大叔用22根1米长的栅栏围一块长方形花圃,怎样围面积最大?教材给出了“根据题中的已知条件,你能想到什么?你打算怎样解决这个问题?”这两个提示后,直接呈现了表格(如下表),让学生先列举出所有的长和宽,再求出面积后找到答案。
你能先列举出长方形的长和宽,再找出面积最大的长方形吗?
长方形的长与宽的和是22÷2=11(米)。
检查列举出的结果,看看有没有重复或遗漏。
答:长____米、宽____米时,面积最大。
这样的呈现,学生感受不到为什么要用一一列举的策略,也感受不到为什么要不重复、不遗漏,指向不了一一列举策略的本质,大部分的学生只是根据提示和表格去完成此题。这样的学习对于学生来说是肤浅的,只能解决某些题,起不到举一反三的作用。
又如,用画图的策略:

7.新庄小学的操场原来是一个正方形(如右图所示)。扩建校园时,操场的一组对边各增加18米,这样操场的面积就增加了900平方米。原来操场的面积是多少平方米?(先在图上画一画,再解答)
8.张宁和王晓星一共有画片86张。王晓星给张宁8张后,两人画片的张数同样多。两人原来各有画片多少张?(先把已知条件在线段图上表示出来,再解答)

题目直接给出提示,那么学生就不会思考,直接运用画图的方法解题。如果没有这样的提示,学生会想到用画图的策略吗?孩子的学习就像学走路一样,大人不放手,孩子永远也学不会。教学是让学生从“误”到“悟”,从“混沌”走向“有序”,教材应该少给一些暗示,让学生慢慢感悟到策略的价值,这才是学习策略的价值。
3.题少类多,学生不易建构
如四年级下册的画图策略,教材中只安排了2个例题,例1是和差问题,例2是面积问题(已知一个长方形的面积和一条长,当长增加几米,面积也增加几平方米,求原来长方形的面积)。与例题配套的习题有16题,16题里包含的类型很多,与例1和例2一样的只有第1题、第6题和第12题,其余都是对例1与例2的变式与拓展。对此,教材建议安排3课时。事实上,这样的编排不利于学生对这个策略的感知和建构,因为新知都没有构建好,何谈应用。
二、解决问题的策略的教学建议
1.激发内需,自主构建
小学生是以形象思维为主,逐步过渡到抽象思维,而解决问题的策略是抽象的,教师一定要让学生感受到策略的优越性,以及学习策略的必要性,让学生有一个自主构建的过程,从而自觉地运用策略解决问题。因此,在这样一个过程中,激发学生的内需是相当重要的。如对于一一列举的策略,我是这样教学的:
【第一环节】
师(出示复习题):两个整数相加,和是10,可能是几加几?
生1:3+7=10。
生2:5+5=10。
……
师:能把所有的可能都列举出来吗?
生3:能。3+7=10,5+5=10,1+9=10,4+6=10,2+8=10……
师:有没有一种办法,能做到不重复、不遗漏?
生4:按一定的顺序列举。
师:为什么要按一定的顺序列举,有何好处?
【评析:第一环节没有直接讲例题,而是让学生初步感受到了一一列举策略,以及感受要按一定的顺序列举,为后面的学习奠定了基础。】
【第二环节】
师:刚才我们把所有的情况都一个一个列举出来了。想一想,什么情况下要把所有的情况一个一个列举出来?
师(出示两道题目。A题:一个长方形的长和宽都是整数厘米,面积是12平方厘米,长可能是几厘米?B题:一个长方形的长和宽都是整厘米数,面积是12平方厘米,长有几种可能?):哪一题需要把所有的情况列举出来?
生1:A题不需要一一列举,B题需要一一列举。要求有几种可能,就要把所有的情况一个一个列举出来,才能找出一共有几种。
师:也就是当求一共有多少种可能时,要一一列举出来。
【评析:这一环节让学生感知什么情况下要一一列举。】
【第三环节】
师(出示例1:王大叔用22根1米长的栅栏围一块长方形花圃,怎样围面积最大?):你准备用什么方法解决?
生1:一一列举。
师:这里不是求一共有多少种情况,为什么要一一列举?
生1:虽然不是求一共有多少种,但是要求面积最大的,必须把所有可能的面积求出来,再找出最大的面积,如果不是一个一个列举出来,得到的答案可能不是最大的。
通过三个教学环节,学生在层层对话中自然而然地知道一一列举是什么,为什么要一一列举,什么情况下可以用一一列举的方法,运用一一列举的策略就成为自然的内需,而不是教师告诉他们的。
2.跨越课时,分类安排
有效的教学一次只能教学少量的策略,但教材编排的例题少,题型多,课时少。因此,教师要解决这个弊端,就不能按着教材的顺序走,要一类一类地呈现策略。如,在第一课时教学和差问题以及变式;第二课时拓展到和倍问题以及变式;第三课时教学例2以及“试一试”,并完成相应的练习;第四课时教学例2的变式题,即由一条边扩大变成一条边缩小,再扩展到正方形;第五课时教学生活中的一些应用,如教材中的队列问题、倒推问题和种树问题。
3.总结回顾,融会贯通
虽然从三年级起每一册教材都会有解决问题的策略,但是每一册的教学重点是不同的,那么对于这些策略的应用就要落在平时的教学中,要在常态的课堂中加强总结和回顾,只有总结了才能将知识深化,学生才会灵活运用策略。如在教学转化的策略后,让学生进行总结。
师:在解例1时,是把不规则的图形转化成了什么图形?
生1:把不规则的图形转成了规则的图形。
师:课本上哪些题目是把不规则图形转化成规则图形?
师:请尝试出题,画出一些可以转化成规则图形的不规则图形。
展示学生的作品,再对所有的作品进行分类,学生得出两类:一类是周长的转化,把求不规则图形的周长转化成求规则图形的周长;另一类是面积的转化,把求不规则图形的面积转化成求规则图形的面积。
通过总结让学生明确转化策略的作用——把不规则的图形转化成规则的图形,进一步感知策略的用途。
解决问题的策略教学最终的落脚点是应用,为的是达到学以致用的效果。因此教师在教学中要基于教材,又要改编教材,让策略真正成为学生能够解决问题的策略。
