KPCA-KELM在短期交通流量预测中的应用

2018-09-11王秋莉

江苏大学学报（自然科学版） 2018年5期

李军, 王秋莉

(兰州交通大学自动化与电气工程学院, 甘肃兰州 730070)

交通流量预测是智能交通系统(intelligent transportation systems, ITS)的一个重要组成部分,准确的交通流量预测有助于交通管理部门实施相应的措施以提高城市交通路网的运行效率.

受环境、行人等随机因素的干扰,城市交通流量具有高度非线性、复杂性和时变性等特点.根据原理的不同,其预测方法可分为基于确定数学模型的方法和基于知识的智能模型预测方法[1-2].目前,神经网络与支持向量机(SVM)等借助计算智能的方法已在交通流量预测方面取得许多成功应用[3-6].文献[3]给出小波神经网络交通流量预测模型,取得了较好的预测效果;文献[4]将SVM方法应用于高速公路的交通流量单步及多步预测中.文献[5-6]分别将SVM、最小二乘支持向量机(LSSVM)应用于短时交通流量单步预测中,取得了较好的预测效果.

极限学习机(ELM)是由HUANG G. B.等[7]提出的用于单隐层前馈网络(SLFNs)的快速学习算法,文献[8-9]将ELM方法成功应用于交通流量单步预测中.当ELM的隐含层节点未知时,采用核矩阵方法替代之,形成核极限学习机(kernel extreme learning machine, KELM)方法[10],其优点是仅需选择适当的核参数与正则化系数,通过矩阵运算就可获得网络的输出权值.KELM方法改善了ELM随机给定和隐含层偏置造成输出结果不稳定的缺点,同样可考虑将其用于短期交通流量预测中.

进一步考虑特征提取技术[11-12],文献[13]将核主元分析(kernel principal component analysis, KPCA)与SVM结合的方法用于混沌时间序列预测中,在一定程度上有效提高了预测精度.

借鉴KPCA-SVM,ELM等机器学习方法在时间序列预测、短时交通流量预测等方面的成功应用,为提高短时交通流量预测的收敛速度、预测精度,文中提出KPCA-KELM预测方法,并将其应用于某地区公路观测站的实测数据实例中.在同等条件下,将新方法与KELM,KPCA-SVM以及SVM等方法进行对比,以验证新方法有效性.

1 KPCA-KELM方法

PCA是一种被广泛采用的特征提取方法,它仅涉及在数据的原始空间上进行线性化处理的技术.KPCA将原始输入数据经变换后,在高维非线性特征空间上使用PCA方法计算主成分.文中提出了KPCA-KELM预测方法，此方法将KPCA方法用于KELM交通流量预测模型的数据预处理中,按照相关度选取非线性特征作为模型的输入.

给定训练数据集{xi,yi|xi∈Rm,yi∈Rn,i=1,2,…,l}，构建训练输入矩阵X∈Rl×m、输出矩阵Y∈Rl×n.核方法将输入数据xi映射到高维非线性特征空间中,即φ:x∈Rm→φ(x)∈F⊆RM,定义核函数为k(xi,xj)=φ(xi)Tφ(xj).

1.1 KPCA方法

定义满足Mercer条件的核矩阵K=XTX,其中X=[φ(x1)φ(x2)…φ(xl)].文中核学习方法选用高斯核函数,即

k(xi,xj)=exp{-‖xi-xj‖/2σ2},

式中σ为高斯核函数的宽度.

对于输入空间的l个样本xi,i=1,2,…,l,协方差矩阵Σ可表示为lΣ=XTX,其元素为

首先对核矩阵K与协方差矩阵Σ分别进行特征值分解,即

K=VΛlVT,lΣ=UΛNUT,

(1)

式中正交矩阵V,U的列向量vi,ui分别为K,lΣ的特征向量.

利用K与lΣ的对称性,能将lΣ的任意特征向量u与特征值λ变换为K所对应的特征向量Xu与特征值λ.令t=rank(XXT)=rank(XTX)≤min(N,l),则U的前t列特征向量构成的矩阵Ut可表示为

(2)

其中假定K与lΣ的前t个非0特征值是按降序排列的.

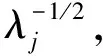
(3)

考虑式(3),若定义Ud是特征空间中由前d个特征向量ud所张成的子空间,训练数据φ(x)在该子空间上的d维向量投影为

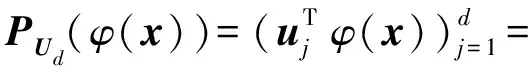
(4)

式(4)即KPCA方法的核心.文中核函数采用高斯核函数.

KPCA算法具体步骤如下:

1) 计算X=[φ(x1)φ(x2)…φ(xl)]T所形成的核矩阵Kij=(k(xi,xj)),i,j=1,2,…,l.

2) 对核矩阵K进行中心化处理,即

(5)

式中j为所有元素均为1的列向量.

(6)

4) 由式(3),计算前d个特征向量v的相应对偶向量表示,即计算前d个对偶向量α,可得

(7)

5) 在特征空间中,计算训练数据φ(x) 在前d个对偶特征向量上的投影,即计算非线性主元,可得

(8)

1.2 KELM方法

KELM是ELM的非线性延伸,通过最小化训练误差和输出权值范数对网络进行训练.本节在ELM的基础上,给出KELM的学习方法[14].

对于含L个隐层节点的SLFNs,给定l组训练样本数据集{xi,yi|xi∈Rm,yi∈Rn,i=1,2,…,l}，其输出表达式为

(9)

式中:βi为第i个隐含层节点与输出层节点的权值向量;hi(x)为第i个隐含层节点的输出函数K(x;wi,bi).本节隐含层节点选用RBF节点,其激活函数形式为

K(x;wi,bi)=exp(-bi‖x-wi‖2).

矩阵形式可表示为

Hβ=T,

(10)

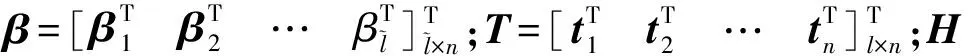
综上所述,ELM的学习算法相当于求解式(10)的最小二乘解β,则输出权值矩阵的最小二乘解为

(11)

为提高网络的稳定性与泛化能力,根据岭回归的思想引入正则化参数Υ,对网络输出权值矩阵β的解进行约束,防止出现“过拟合”现象.因此,式(11)可表示为

(12)

ELM的网络输出表达式为

(13)

在式(12)，(13)的求解过程中，若隐含层节点数目未知，为避免随机赋值导致ELM输出不稳定的情况，考虑引入核方法，用核函数表示隐含层非线性特征映射，应用Mercer条件，定义核矩阵KELM=HHT,其元素为KELM(i,j)=h(xi)·h(xj)=k(xi,xj),用核矩阵KELM代替ELM隐含层节点,由式(12)可得KELM网络输出为

KELM方法的核函数k(xi,xj)类型选择线性核函数.

2 交通流量预测实例

智能交通系统网络是在道路的路口安装无线传感器,通过各个点的传感器采集路面数据信息并共享形成数据网络.按照时间序列建模的方式,将KPCA-KELM方法应用于不同地区的短期交通流量预测实例中,所建立的预测模型为

(14)

式中:Δ为预测步长;xt为历史时间序列值构成的多维输入向量,即xt=(xt-1,xt-2,…,xt-D),D为嵌入维数.

本节试验均采用均方根误差(root mean square error,RMSE)衡量预测精度,计算式为

(15)

2.1 实例1

试验选取北京交通管理局UTC/SCOOT系统所记录的9条线路,分别标号为Bb,Ch,Dd,Fe,Gd,Hi,Ia,Jf,考虑到检测器或变送器的故障,屏蔽了存在空流量数据的日期,最终得到25 d的交通数据.以Ch线路采集的车流量数据为实例,将每15 min的交通流量数据汇集,共得到2 400个采样点,与文献[15]一致,取前2 112组数据作为训练样本,其余作为测试样本.选取嵌入维数m=10.参数设定如下:KELM,KPCA,LSSVM,SVM均各自选取高斯核函数,核函数宽度σ=0.5;KELM正则化参数Υ=200;对比试验中,SVM,LSSVM方法惩罚因子C=0.5,ε=0.01;KPCA-SVM,KPCA-LSSVM,KPCA-KELM方法中,KPCA的非线性主元数目为15,SVM选取线性核函数;不同方法分别进行提前15,30 min的预测结果对比由表1给出.

表1 实例1不同方法预测结果对比

由表1可见,与SVM等方法相比,KELM方法的预测精度略有提升,KPCA-KELM组合预测方法则显示出了较高预测精度.图1,2分别为实例1不同方法提前15,30 min的预测结果,由图1,2可见,文中方法呈现出较好的预测效果.

图1 实例1提前15 min交通流量预测

图2 实例1提前30 min交通流量预测

2.2 实例2

实例2选择西雅图华盛顿大学的ITS研究组的交通数据采集与分布(traffic data acquisition and distribution, TDAD)数据库提供的数据[16],网址为www.its.washington.edu/tdad/.该数据有4个不同的探测器(ES-088D, ES-855D, ES-708D和ES-645D),这4个探测器分别位于美国西雅图地区的3个洲中的5(I-5),90(I-90)和405(I-405),本试验选择ES-855D记录交通流量数据为例,时间间隔为15 min,选取前14 d共1 344个数据作为训练集输入,最后7 d共672个数据作为测试样本.选取其嵌入维数m=24.图3给出了探测器ES-855D等在实际地图上的位置.

图3 探测器位置

本节试验中,将各方法结果调至最优,单步与多步预测试验参数相同.参数设定如下:KELM,KPCA,LSSVM,SVM均各自选取高斯核函数,核函数宽度σ=1;KELM正则化参数Υ=300;对比试验中,SVM,LSSVM方法惩罚因子C=0.5,ε=0.01;KPCA-SVM,KPCA-LSSVM,KPCA-KELM方法中,KPCA的非线性主元数目为10,SVM选取线性核函数;预测结果对比由表2给出.