扣入式与缠绕式止屈器联合作用的止屈效率

余建星， 安思宇， 段晶辉， 蒋梅荣， 韩梦雪

(天津大学 水利工程仿真与安全国家重点实验室， 天津 300072)

0 引 言

近年来，我国石油产量稳步提升，其增量主要来自海洋石油的开发。油气输送的主渠道是海底管道，海底管道保证了整个系统的正常运行，其稳定性和安全性对于海洋油气开发极为重要。海底管道在外部水压的作用下有可能发生屈曲压溃[1]。通常，海底管道的屈曲传播压力只有其压溃压力的18%～25%[2]，这意味着管道压溃压力远大于其传播压力，只需比管道压溃压力小得多的外部压力就会产生屈曲传播。

止屈器是一种能提高管道局部环向刚度的厚壁圆环，能够通过加强管道局部的环向强度阻碍屈曲沿管道传播，使屈曲传播不能跨越止屈器，从而将局部屈曲限制于2个止屈器之间。扣入式止屈器和缠绕式止屈器是2种常见的海底管道止屈器结构形式：扣入式止屈器由于其止屈效果好、成本低的特点，在管道铺设过程中的应用相对广泛[3]；缠绕式止屈器具有避免应力集中、安装过程简单、适应面广等特点，同样得到了较多的应用。

在开发海洋石油的过程中，海洋工程作业、船舶起抛锚作业等都会造成海底管道的屈曲变形。破损的管道需要尽快进行加固和维护，避免造成管道屈曲压溃等更大的危害。但由于管道产生了变形，扣入式止屈器难以进行拆卸或更换，给管道加固和维护带来了一定的困难。缠绕式止屈器的安装过程决定了其具有易安装、适应面广的特点，可以通过在扣入式止屈器或管道上安装缠绕式止屈器，即通过二者的联合作用，提高止屈器的止屈效率，进而提高管道的稳定性和耐久性。相比于传统的单独止屈器，联合作用式止屈器具有易加工、易安装、结构简单的特点。LEE[3]、PARK等[4]、HUANG[5]等国内外学者对扣入式止屈器和缠绕式止屈器进行了充分的研究，得到了大量相关数据和重要结论。但对于扣入式止屈器和缠绕式止屈器联合作用的止屈效率，较少有学者进行过深入研究。本文利用Abaqus软件对扣入式和缠绕式止屈器联合作用的止屈效率进行研究，对多影响因素下两者联合作用止屈器的作用效果进行分析。

1 止屈器的止屈特性

1.1 止屈效率

当外部水压达到一定数值后，管道屈曲传播到止屈器时可能会穿越止屈器继续传播，从而造成管道整体破环。穿越压力是使屈曲传播穿越止屈器所需要的最小外部压力。为了便于表示止屈器的止屈效果，KYRIAKIDES[2]提出的止屈器效率的计算公式为

(1)

式中：η为计算得到的止屈效率；PX为止屈器的穿越压力；PCO为管道屈曲压溃压力；PP为屈曲传播压力。

1.2 穿越模式

图1 止屈器穿越模式

屈曲传播在穿越止屈器时会呈现不同的穿越模式，根据不同的止屈器试验结果可分类如下：(1)平行穿越模式。止屈器的穿越压力较小时可能会发生平行穿越，如图1 a)所示，屈曲传播跨越了止屈器向管道下游传播，止屈器下游管道的屈曲方向与止屈器上游管道的屈曲方向相同，即发生了平行穿越。(2)U型穿越模式[6]。止屈器的穿越压力较大时可能会发生U型穿越，如图1 b)所示，屈曲传播跨越了止屈器向管道下游传播，止屈器上游管道发生U型屈曲，并以U型穿越止屈器。

2 有限元分析及数值模型

2.1 体积加载方式

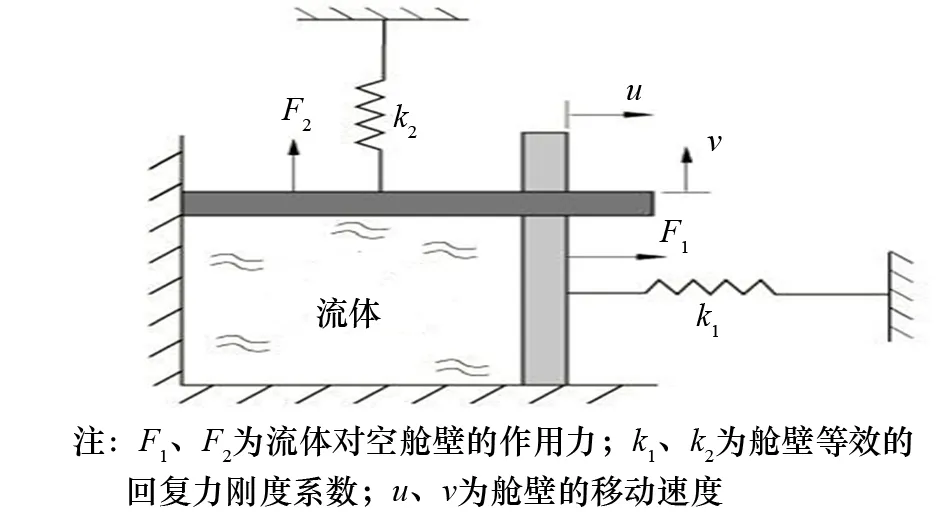
图2 静水流体单元实例

为真实地模拟管道模型在水压作用下的屈曲传播及止屈器的穿越，加载方式采用一种特殊的体积控制加载方式。为此，引入Abaqus中的静水力流体单元——F3D4单元，通过静水力流体单元确定在结构物周围定义区域内的体积变化，便可以将压力加载转变为体积加载，压力数值可通过体积的变化得到。

体积加载通过静水流体单元实现。静水流体单元，即流体弹簧单元，要求在空间上由若干个面形成一个封闭的空腔，在指定的面上与受载结构外表面耦合，从而由结构变形情况确定空腔的体积变化，进而确定作用于结构上流体压力的大小，如图2所示。静水力流体单元用来模拟被流体充满的腔体结构，这种结构的响应不仅取决于外部的载荷，还与内部流体的压力变化有关，而内部流体的压力变化又会受到腔体变形的影响。静水力流体单元可以实现这种结构变形与内部流体压力变化之间的耦合作用。

2.2 本构关系

管道及止屈器材料的弹性模量及泊松比可以通过测量得到，并利用Ramberg-Osgood方程拟合得到材料的屈服应力-塑性应变曲线：

(2)

式中：ε为应变；σ为应力；σy为材料的屈服应力；E为材料的杨氏模量；取n为10.7，得到相应材料属性。

图3 扣入式止屈器有限元模型

2.3 扣入式止屈器

2.3.1 扣入式止屈器模型

管道模型如图3所示，沿长度方向分为止屈器上游段、安装止屈器区段和下游屈曲传播段3部分。其中，上游段端部设置局部椭圆度缺陷以触发管道局部屈曲，局部缺陷所在处的椭圆形截面也被设置为对称面[7]。

2.3.2 扣入式止屈器结果校验

天津大学深海全尺寸压力试验舱如图4所示，可对带有止屈器的管道进行全尺寸试验，得到管道在止屈器作用下的压溃压力和屈曲传播压力。管道屈曲穿越扣入式止屈器全尺寸试验如图5所示。

图4 深水全尺寸压力舱 图5 管道屈曲穿越扣入式止屈器全尺寸试验

通过管道全尺寸试验，对325 mm×10 mm、406 mm×10 mm管道在不同长度或厚度的扣入式止屈器作用下的屈曲穿越压力进行了试验研究，得到穿越压力的试验值。采用有限元法，选择其中6组进行建模分析，并将穿越压力的数值模拟结果与试验结果进行对比，见表1，可以看出：试验结果与模拟结果很接近，说明有限元模拟方法是可行的。

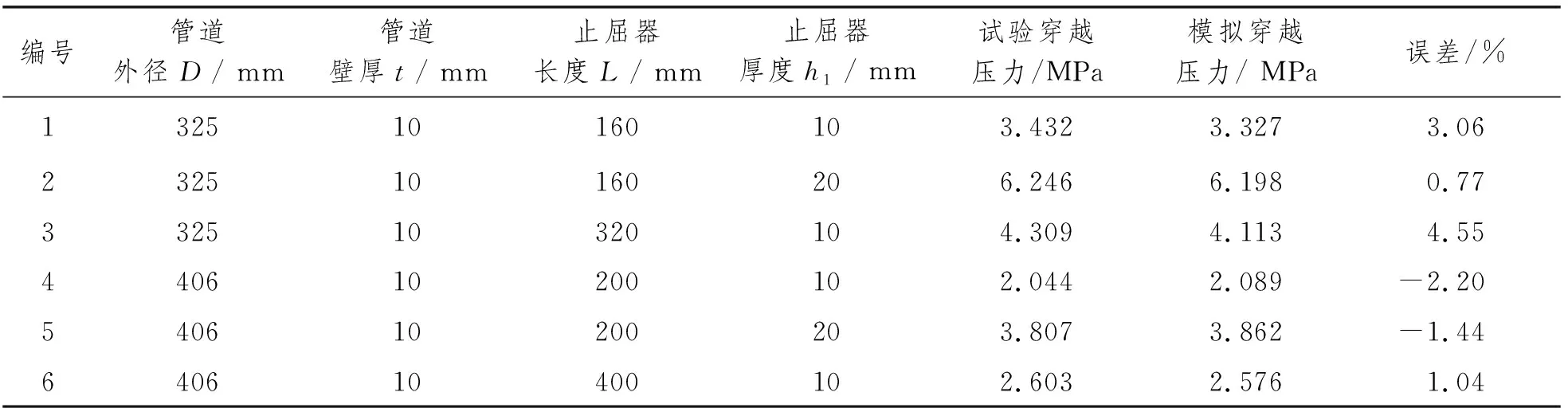
表1 扣入式止屈器有限元模拟穿越压力与试验穿越压力对比

算例1的屈曲平行穿越扣入式止屈器如图6所示。在加载过程中，有着初始椭圆度的模型端部首先压溃，随后屈曲沿管道轴向传播。随着屈曲传播到达止屈器附近时，加载水压逐渐上升，止屈器阻碍了屈曲传播的进行。直到加载水压接近止屈器的穿越压力时，止屈器的截面才开始发生显著的椭圆化变形，同时管道的下游段也产生变形。在加载水压不断上升的同时，止屈器的变形也逐渐扩大。当止屈器的变形扩大到一定程度时，止屈器完全失效，管道屈曲可顺利地通过止屈器继续向管道下游传播。此时加载水压到达峰值，对应的值即为止屈器的穿越压力。

图6 止屈器

2.4 缠绕式止屈器

2.4.1 缠绕式止屈器有限元模型

图7 缠绕式止屈器

建立缠绕式止屈器的简化模型——多环式模型。多环式缠绕止屈器模型实际上是对全缠绕式止屈器模型在几何上的一种近似。它是用一系列独立的短钢棒代替一根连续的长钢条，将其缠绕到管道上形成一系列封闭并紧邻的独立圆环。由于每个圆环在平面内都是对称的，因此管道与止屈器均可采用 1/2 对称模型，从而把有限元分析问题的规模减小了一半。利用多环模型的缠绕式止屈器截面如图7所示。

2.4.2 缠绕式止屈器结果校验

为了验证模型的正确性，以HUANG[5]的试验结果为参照，建立与其试验管件尺寸相同的管道及止屈器模型，并选用相同的材料SS-304，对穿越压力的计算结果进行对比，结果见表2。

表2 缠绕式止屈器有限元模拟穿越压力与试验穿越压力对比

由表2可知：试验结果与有限元模拟结果差距很小，说明有限元模拟方法可行，可以用此模型对缠绕式止屈器进行研究。

2.5 扣入式与缠绕式止屈器联合作用

扣入式和缠绕式止屈器联合作用的情况有2种：一种是扣入式与缠绕式止屈器并行排布，另一种是扣入式止屈器外附加缠绕式止屈器。

2.5.1 并行排布式止屈器

并行排布式止屈器是将扣入式与缠绕式止屈器在管道轴向方向上串联起来的一种止屈器，两者共同作用来限制管道的屈曲传播，具有更灵活的止屈功能。在这种模型中，止屈器间距对其止屈效率有一定的影响。建模中取紧贴、间距2倍管道直径、间距4倍管道直径、间距6倍管道直径、间距8倍管道直径等5种情况进行计算。紧贴并行排布式止屈器的截面如图8所示，间距为2倍管道直径的并行排布式止屈器如图9所示。

图8 紧贴并行排布式止屈器 图9 间距为2倍管道直径的并行排布式止屈器

2.5.2 叠加式止屈器

扣入式止屈器外附加缠绕式止屈器(即叠加式止屈器)如图10所示。

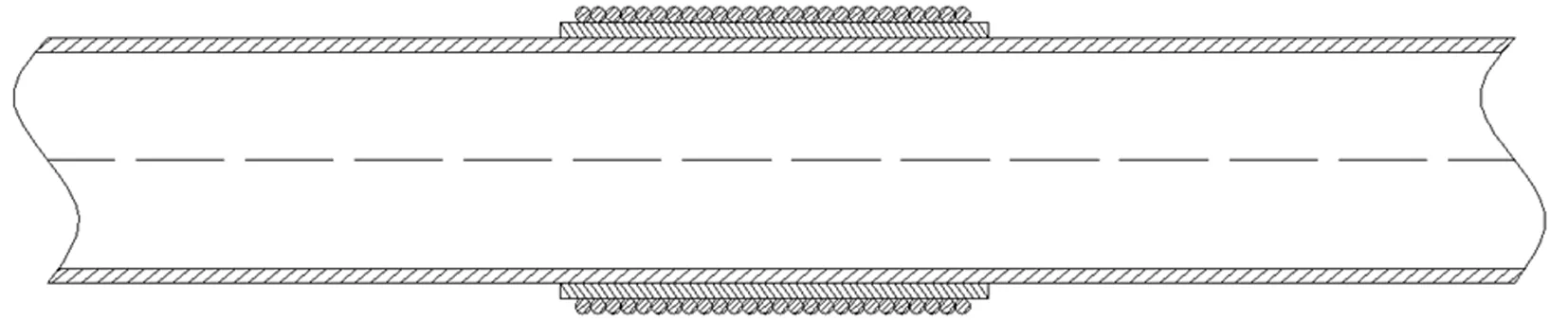
图10 叠加式止屈器

为了达到控制变量的要求，扣入式止屈器外附加缠绕式止屈器所用材料质量应与单独扣入式或单独缠绕式止屈器相同，扣入式止屈器的壁厚长度及缠绕式止屈器的壁厚匝数可由式(3)求得

(3)

式中：D为管道外径；t为管道壁厚；L为单独扣入式或单独缠绕式止屈器有效长度；h1为扣入式止屈器壁厚；h2为缠绕式止屈器壁厚；L1为扣入式止屈器长度；N2为缠绕式止屈器匝数。

3 联合作用式止屈器止屈效率

3.1 建模参数

管道及止屈器的材料均采用海底管道常用材质API 5L X65型钢，应力-应变关系采用基于流动理论的Ramberg-Osgood模型。计算采用的管道尺寸见表3。压溃压力取初始缺陷为0.1%椭圆度管道的压溃压力，可得压溃压力为21.27 MPa。

表3 管道模型尺寸

3.2 计算结果

3.2.1 基本型式止屈器

根据控制变量的要求，有限元管道的各项尺度应保持一致。对于止屈器而言，可以通过保证其质量总和相等，并计算不同止屈器的穿越压力来研究其止屈效率。这要求各类止屈器在相同的壁厚条件下，所用总钢材量相同。分别对壁厚为4 mm、5 mm、6 mm、7 mm的各类止屈器进行计算。对于每种壁厚，保证各类止屈器有效长度相同。分别取单独缠绕式止屈器匝数N为5、10、15、20、25。联合作用式止屈器选用2类基本形式：对并行排布式止屈器中的紧贴并行排布式止屈器进行计算；对扣入式止屈器壁厚分别为3 mm、4 mm、5 mm、6 mm，缠绕式止屈器壁厚为2 mm的叠加式止屈器进行计算。联合作用式止屈器的止屈器长度(匝数)也遵从控制变量的原则。计算结果如图11～图14所示。

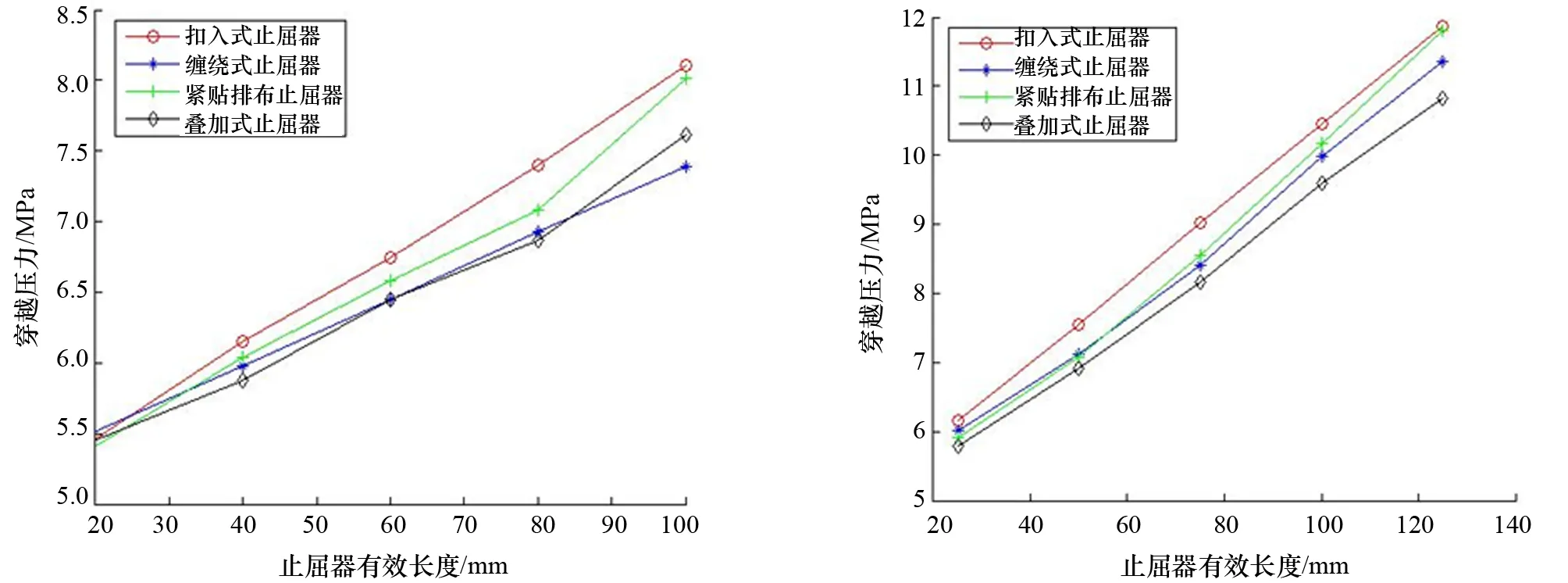
图11 4 mm壁厚各止屈器穿越压力随有效长度的变化 图12 5 mm壁厚各止屈器穿越压力随有效长度的变化

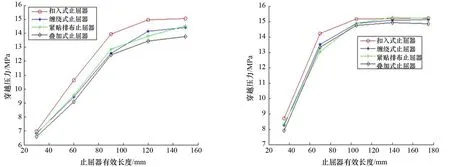
图13 6 mm壁厚各止屈器穿越压力随有效长度的变化 图14 7 mm壁厚各止屈器穿越压力随有效长度的变化

由图11～图14可以看出：4种类型止屈器止屈效率的变化趋势相似，止屈器的止屈效率随止屈器截面壁厚的增加而增加，但增加趋势不是线性的。在一定的壁厚范围内，增大止屈器的壁厚对止屈效率的提高作用非常明显，但当截面壁厚达到一定值后，止屈器止屈效率增长趋势变缓，逐渐趋于一个稳定值。改变止屈器的有效长度(匝数)时，止屈效率有着类似的变化趋势。

3.2.2 并行排布式止屈器

对于并行排布式止屈器的止屈效率，在计算了两者紧贴时止屈器模型的穿越压力及止屈效率后，在止屈器壁厚为6 mm的条件下，计算和分析两止屈器间距对并行排布式止屈器止屈效率的影响。分别对间距为2倍、4倍、6倍、8倍管道直径的并行排布式止屈器进行计算，结果见表4。

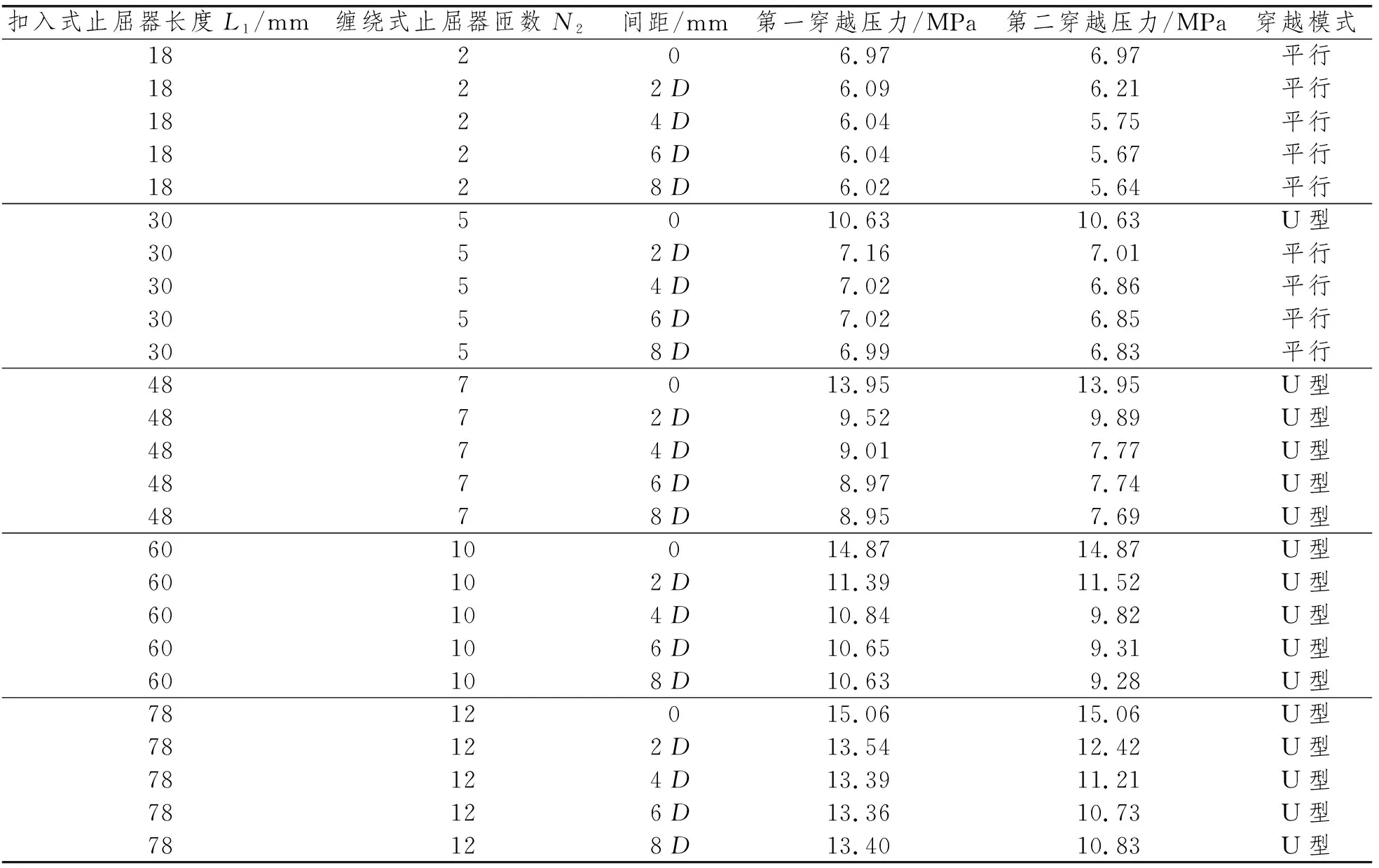
表4 6 mm壁厚并行排布式止屈器穿越压力随尺度变化关系

屈曲U型穿越2倍管道直径间距的并行排布式止屈器如图15所示。图16为2倍管道直径间距的并行排布式止屈器的管道加载曲线。对于并行排布式止屈器，由于止屈器之间存在间距，因此模型加载曲线的后段会存在2个峰值。管道前端压溃后，由于压溃导致管道缺陷，较低的外部压力就可以维持管道的屈曲传播。屈曲传播到扣入式止屈器附近，由于止屈器对管道结构及屈曲失效的限制作用，管道压溃压力逐渐增大，直到外部压力上升至图16中所示的第1个峰值，扣入式止屈器失效，屈曲得以穿越止屈器继续沿管道传播。曲线后段第1个峰值对应的值即为扣入式止屈器的穿越压力，称为第一穿越压力。屈曲穿越扣入式止屈器后，由于还未遇到缠绕式止屈器的限制，会重复上述过程，直到屈曲传播到缠绕式止屈器附近。与扣入式止屈器类似，缠绕式止屈器同样会增大局部管道的压溃压力，曲线后段的第2个峰值即为缠绕式止屈器的穿越压力，称为第二穿越压力。

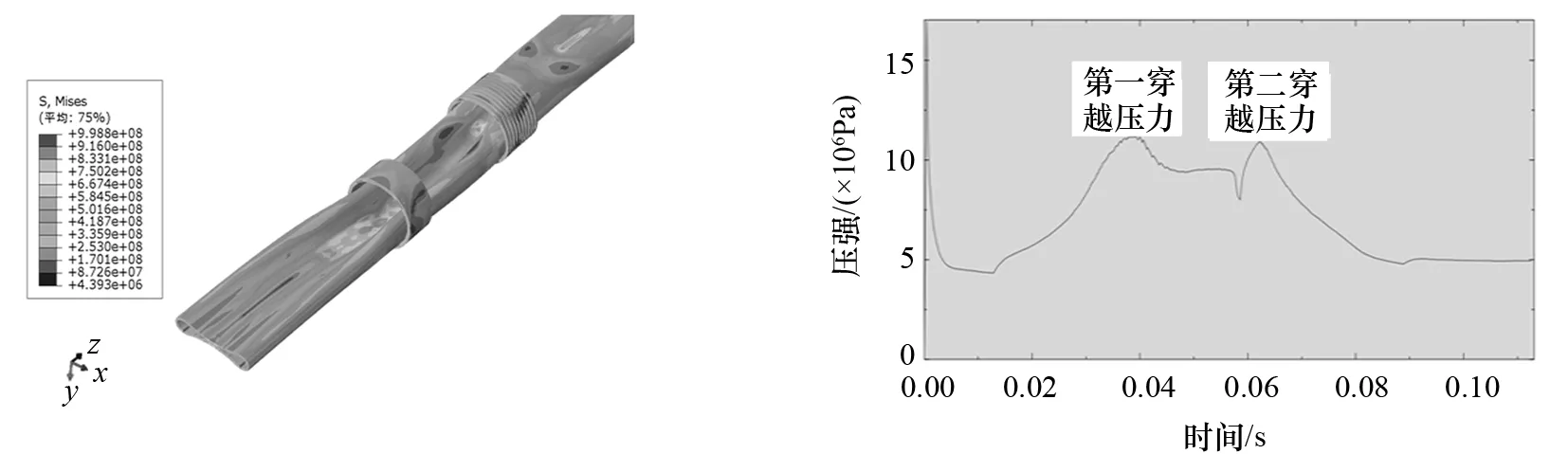
图15 屈曲U型穿越2倍管道直径间距的并行排布式止屈器 图16 2倍管道直径间距的并行排布式止屈器加载曲线

3.2.3 叠加式止屈器

对于叠加式止屈器的止屈效率研究，保持对应单独扣入式止屈器的壁厚为6 mm，改变缠绕式止屈器壁厚及缠绕匝数。通过式(3)进行计算，可以得到叠加式止屈器的6种尺度数值，见表5。对于叠加式止屈器，缠绕式止屈器的匝数只能选取整数，找到与计算得出的缠绕式止屈器匝数最接近的整数作为止屈器的匝数，并代入式(3)继续求解对应扣入式止屈器的长度，可以尽量减小误差。

表5 叠加式止屈器尺度对应表

屈曲U型穿越叠加式止屈器如图17所示。叠加式止屈器的止屈效率计算结果如图18所示，可以看出：对于叠加式止屈器，扣入式止屈器对止屈效率的影响更大，附加的缠绕式止屈器对止屈效率的影响相对较小，但通过增加缠绕式止屈器厚度，仍能明显提升止屈器的止屈效率。

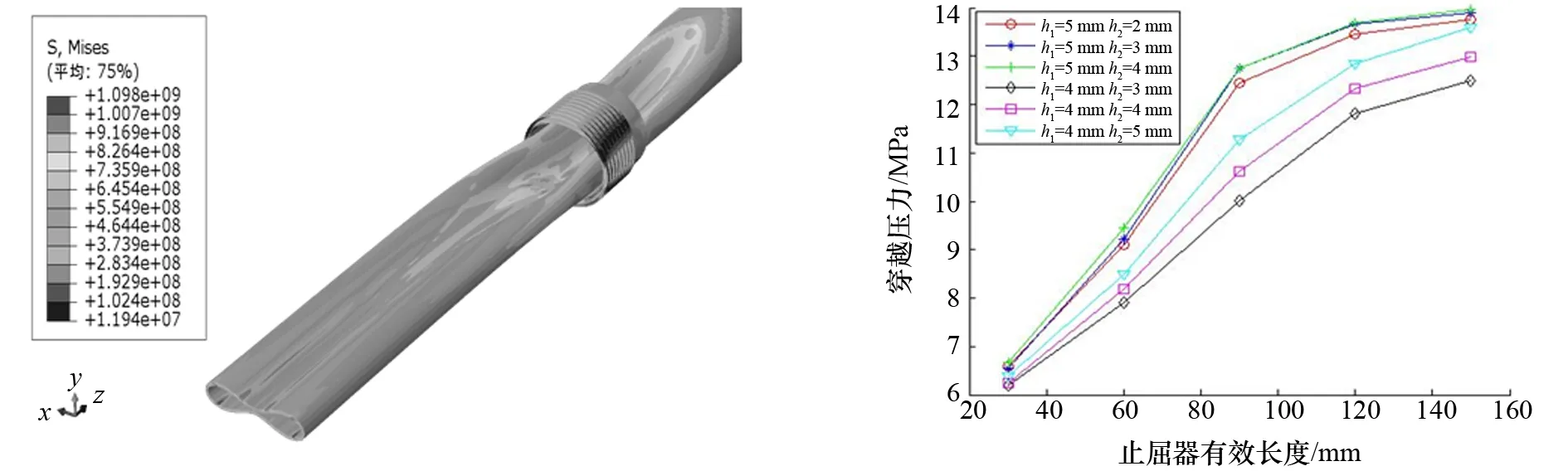
图17 屈曲U型穿越叠加式止屈器 图18 6 mm壁厚各尺度叠加式止屈器穿越压力随止屈器尺度的变化

4 结 论

通过对扣入式和缠绕式止屈器以及并行排布式止屈器和叠加式止屈器的建模计算，以及对影响止屈器止屈效率的长度、匝数、截面壁厚等敏感型因素的分析研究，证明了2种联合作用式止屈器的止屈效果与同等质量的单独扣入式止屈器或缠绕式止屈器差别不大，可以达到较好的止屈效果。说明止屈器联合作用的方式，即采用并行排布式止屈器或叠加式止屈器，在工程实际中可取得较好的应用效果。可以根据实际情况，选择叠加式止屈器或是各种间距的并行排布式止屈器，具有很强的灵活性和实用性。