理论水驱曲线的提出及其与产量递减曲线的关系探讨*
2018-09-11张金庆杨仁锋
张金庆 杨仁锋
(1.海洋石油高效开发国家重点实验室 北京 100028; 2.中海油研究总院有限责任公司 北京 100028)
准确的产量预测是油田产量规划、方案编制及动态跟踪支持的重要依据,是油藏动态管理的核心所在[1-3],决定着投资金额及经济效益。目前较常用的产量预测方法为水驱曲线法及产量递减预测法,很多学者致力于改进上述两种方法以达到更高的预测精度[4-14],但对两种方法的内在联系探讨得不多。在实际应用时,部分学者倾向于应用其中一种方法,部分学者倾向于两者均使用,再根据经验判断如何取值。本文从相对渗透率曲线和物质平衡原理出发,推导出了理论水驱曲线及产量递减曲线(定生产压差及定液量生产条件下),探讨了两者间的关系,并通过油田实际生产资料对理论推导进行了验证。本文研究成果对深化水驱规律及产量递减规律的认识以及提高产量预测精度具有一定的理论价值和借鉴意义。
1 理论水驱曲线的提出
目前很多学者致力于水驱曲线的理论研究,但仍存在适用条件受限、预测结果差异较大等问题[15-18]。本文从相渗曲线及物质平衡方程出发,推导出理论水驱曲线模型,具体推导过程如下。

忽略重力和毛管力的影响,分流量方程为
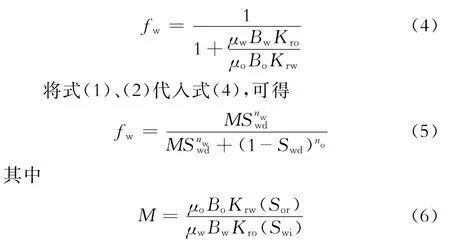
式(5)展示了含水率与出口端含水饱和度的相关关系。Welge方程建立了平均含水饱和度与出口端含水饱和度的相关关系,即

笔者从理论上解决了平均含水饱和度与出口端含水饱和度的相关关系[19],即

张宏友等[20]利用流管法也证明了含水饱和度与出口端含水饱和度可近似为线性关系。
将式(8)代入式(7),可得
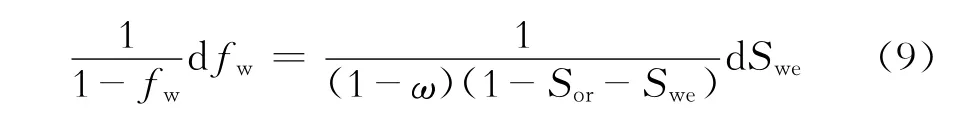
式(9)的初始条件为:Swe=Swi,fw=0。式(9)积分后可得

式(12)的初始条件为:Wp=0,Lp=Np=Npo。
将式(12)分离变量并积分可得
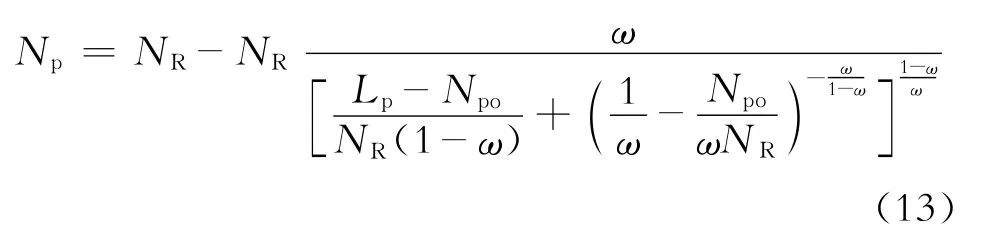
式(13)即为理论水驱曲线模型,其揭示了累积油量与累积液量的相关关系,各项参数的物理内涵十分清晰。

则式(13)可写成

式(18)为理论水驱曲线简化模型。理论水驱曲线模型揭示了累积开发指标与可采储量、相渗参数、Welge方程系数等参数的函数关系。由于Welge方程系数ω与束缚水饱和度、残余油饱和度、油水相指数以及油水黏度比有关[19],因此理论水驱曲线亦与上述参数有关。
2 见水后产量递减曲线的理论推导
油田实际生产过程中常用的工作制度有两种:定液量生产、定生产压差生产,因此分两种情况推导见水后产量递减曲线模型。
2.1 定生产压差条件下产量递减曲线
注水保持地层压力情况下,生产压差基本保持不变,则

平均含水饱和度与出口端含水饱和度相关关系见式(8),将其代入式(23)可得
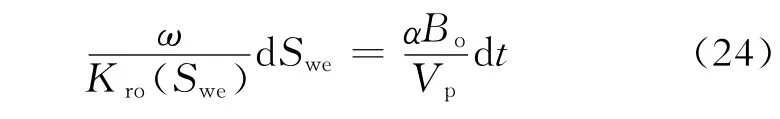
油水两相渗透率由式(1)、(2)表示,代入式(24)积分可得
在t=0时,可得初始产油量为
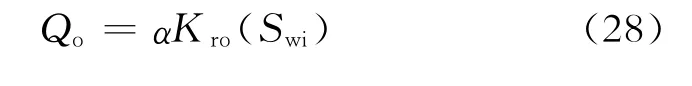

式(31)即为定生产压差条件下推导出的产量递减曲线模型,形式上为双曲递减,递减指数为

当no=1时,n=0,递减模式变为常用的指数递减,此时相渗曲线变成一条直线(通常裂缝发育储层满足no=1);当no→∞时,n=1,递减模式变为常用的调和递减,此时相渗曲线下凹程度较大。
2.2 定液量生产条件下产量递减曲线
根据递减率理论公式
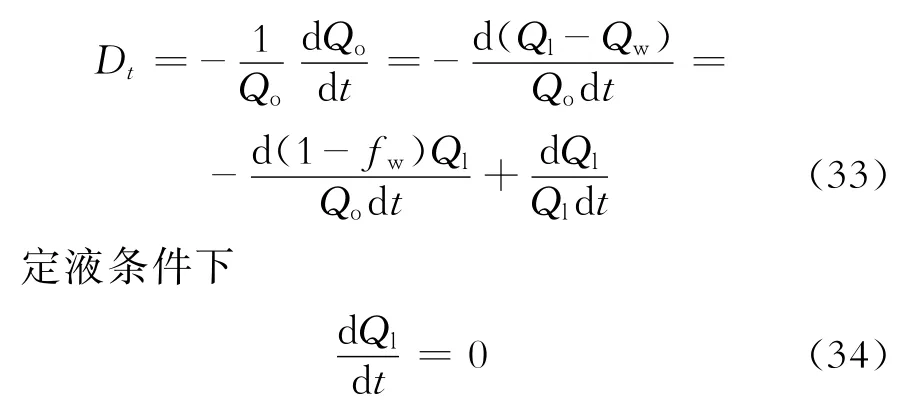
将式(34)代入式(33),可得递减率计算公式为

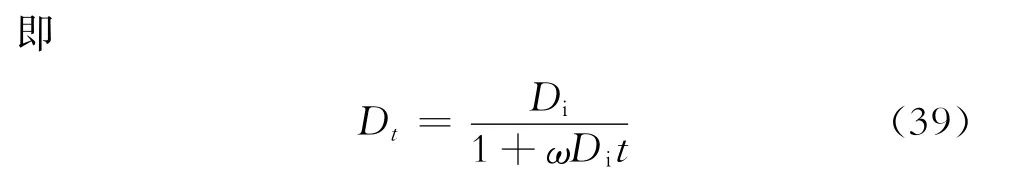
式(39)即为定液量生产条件下推导出的产量递减曲线模型,形式上仍为双曲递减,递减指数为ω。当ω=0时,递减模式变为常用的指数递减;当ω=1时,递减模式变为常用的调和递减。
2.3 递减曲线本质规律分析
调研发现诸多学者开展过产量递减规律的研究[21-29],但推导过程中进行了一定程度的简化,因此忽略出口端含水饱和度与油藏平均含水饱和度的差异,将式(23)简化为
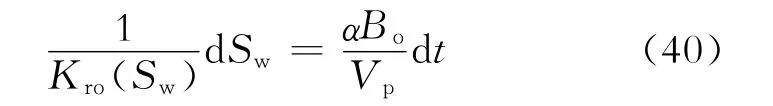
采用不同的相对渗透率曲线表达式,代入式(40)中积分可以得到不同的产量递减方程。表1为不同相对渗透率表达式对应的产量递减模型。表1中,a、b、no分别为相对渗透率曲线拟合系数。
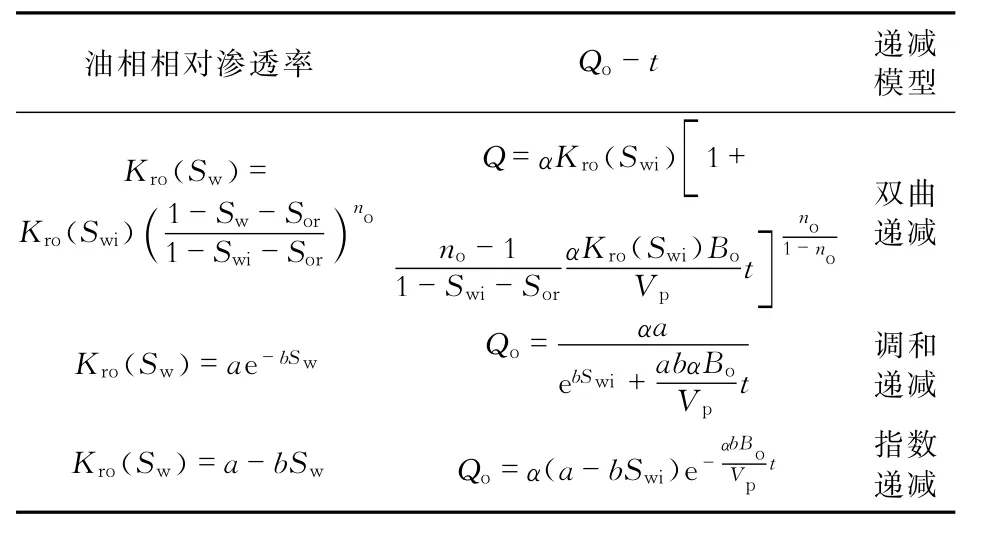
表1 不同相对渗透率表达式对应的产量递减模型Table1 Production-decline models with different relative permeability equations
通过本文的理论分析,可以得出如下2个方面的认识:
1)无论是定生产压差生产还是定液量生产,产量递减通常情况下为双曲递减,满足一定特殊数学条件时才会出现指数递减与调和递减。
2)产量递减影响因素较多,但产量递减反映的内在规律为:随着注水开发的进行,含油饱和度逐渐降低(物质平衡规律的体现)导致油水相对渗流能力的变化(油相相对渗流能力的减弱以及水相渗流能力的增加)。
3 理论水驱曲线与见水后产量递减曲线的关系分析
从上述理论水驱曲线与见水后产量递减曲线的推导过程可以看出,两种方法的理论基础均是相对渗透率曲线和物质平衡方程,即两者本质上应是统一的。
定液量生产条件下在推导出递减率表达式时直接引用了理论水驱曲线方程,其内在规律必然是统一的。下面进一步分析两种方法的内在联系。
式(27)建立的是见水后累计产油量方程,将无水采油期的油量加入后可得

事实上,无论是定液量生产条件,还是定生产压差生产条件,递减规律在通常情况下均为双曲递减规律,因此对比式(41)和式(44)可以得到

与式(32)比较可以得到,递减指数与Welge方程系数相关关系为

即递减指数与Welge方程系数内涵是一致的。
通过上述论证过程可以得出如下认识:
1)理论水驱曲线与产量递减曲线在本质上是统一的,均体现出的是随着开发的进行,含油饱和度逐渐降低导致油水相对渗流能力变化,进而体现在开发指标变化规律上。
2)无论是定压差生产条件还是定液量生产条件,递减规律通常为双曲递减模式,在满足一定的数学条件下可表现为指数递减和调和递减。由于理论水驱曲线推导过程中没有限制条件,因此理论水驱曲线应用范围更大。
3)理论水驱曲线与产量递减曲线方程系数的物理内涵是统一的。在定压差生产条件下,递减指数等于(no-1)/no;在定液量生产条件下,递减指数为ω,ω除与no有关外,还与流度比M和nw有关,但含水趋于1时,ω趋于递减指数n,即(no-1)/no。
4 实例应用
X油田目前超过80%的生产井已见水,整个油田含水率达到37.5%,部分井已达到中高含水阶段。以X-101井为例进行分析,探讨两种方法的统一性。该井生产动态曲线见图1,已表现出见水后产量递减规律,利用理论水驱曲线与产量递减曲线分别对见水后实际生产数据进行拟合。

图1 X油田X-101井生产动态曲线Fig.1 Actual dynamic curves of Well X-101 in X oilfield
基于理论水驱曲线,得出该井累计产油量与累计产液量的函数关系式为
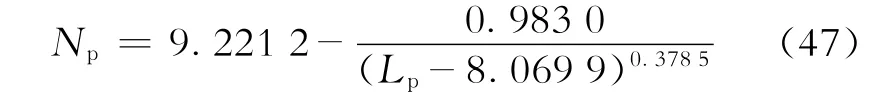
基于产量递减曲线,得出该井累计产油量与生产时间的函数关系式为

通过分析式(47)、(48)可以看出,两种方法得出的可采储量分别为9.221 2 MMbbls(Lp→∞)、9.213 8 MMbbls(t→∞),幂函数指数分别为0.378 5、0.385 1,差别均较小,验证了两种方法内在规律的统一性。
图2为该井利用理论水驱曲线预测的结果,可以看到计算值与实际值拟合精度较高,相关系数超过0.994;利用该井最后一个月的平均产液量2 580 bbls/d,预测到2018年年底累产油达到8.441 2 MMbbls。图3为该井利用见水后产量递减曲线预测的结果,可以看到计算值与实际值拟合精度较高,相关系数超过0.991;预测到2018年年底累产油达到8.456 5 MMbbls,与理论水驱曲线预测结果十分接近。
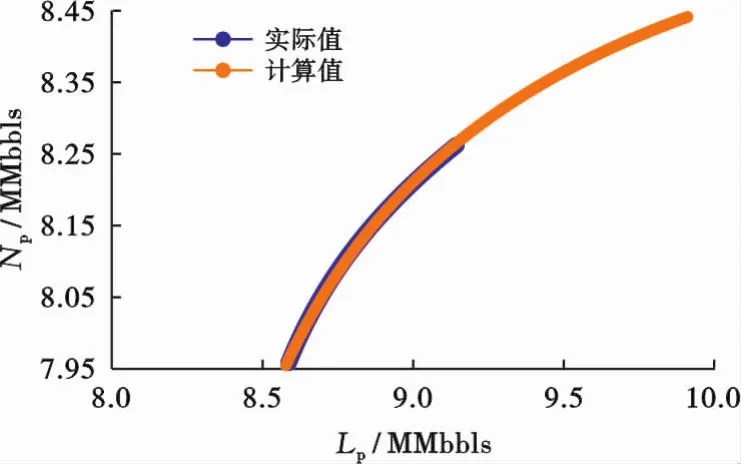
图2 X油田X-101井理论水驱曲线拟合及预测图Fig.2 Analytical waterflooding curves history match and forecasting curves of Well X-101 in X oilfield
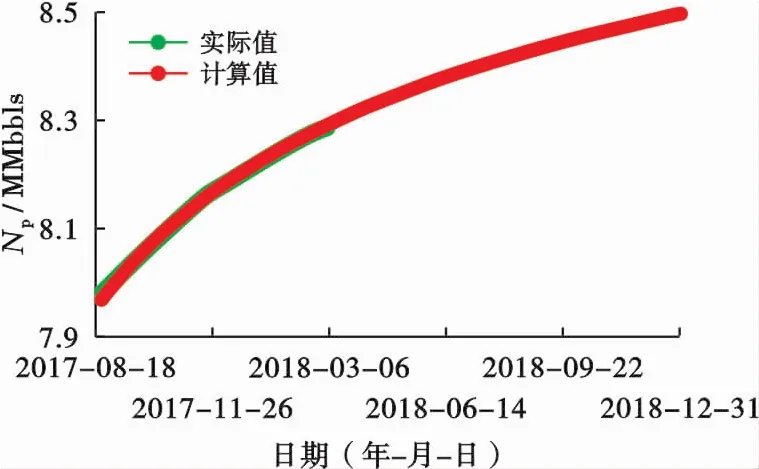
图3 X油田X-101井产量递减模型拟合及预测图Fig.3 Production decline model history match and forecasting curves of Well X-101 in X oilfield
利用两种方法对该油田其他高含水井进行了分析,幂指数差异均较小,也很好地验证了两种方法的统一性。但分析时需要注意:
1)拟合时建议采用高含水阶段数据。
2)整个数据段在选取时务必注意是否存在补孔、卡堵水、改层等调整措施,如存在上述措施则不能直接应用,需要对数据进行劈分后再做分析。
3)两种方法对比时选取的数据段务必保持一致。
5 结论及认识
1)基于相对渗透率曲线表达式及物质平衡方程推导出理论水驱曲线,揭示了累积开发指标与地质储量、相渗参数、Welge方程系数等相关关系;分定液量生产条件、定压差生产条件下推导出见水后产量递减曲线,指出递减指数取决于Welge方程系数,通常情况下递减模式为双曲递减,但在不同的数学条件下可表现出指数递减及调和递减。
2)研究表明理论水驱曲线与产量递减曲线在本质上是统一的,均体现了随着注水开发的进行,含油饱和度逐渐降低导致油水相对渗流能力变化,进而体现在开发指标变化规律上。
3)油田实际生产资料验证了理论水驱曲线与产量递减曲线的本质控制因素与内在统一性。在油藏实际生产过程中,控制条件经常发生改变,注采也不一定平衡,开发前期很多油藏采用衰竭开发,开发后期往往进行综合调整,这些均会影响综合递减率,并体现在公式系数会发生相应改变。
符号注释
Swe—出口端含水饱和度,f;
¯Sw—平均含水饱和度,f;
Swi—束缚水饱和度,f;
Sor—残余油饱和度,f;
Kro(Sw)、Krw(Sw)—油、水相相对渗透率,f;
Kro(Swi)—束缚水条件下油相端点值,f;
Krw(Sor)—残余油条件下水相端点值,f;
ω—Welge方程系数,f;
fw—含水率,f;
Bo、Bw—原油、地层水体积系数;
f′w—含水率导数,f;
N—地质储量,cm3;
Np—累积产油量,cm3;
NR—可采储量,cm3;
Npo—无水采油期累产油量,cm3;
Lp—累产液量,cm3;
Qo、Ql—日产油量、日产液量,cm3;
K—油层绝对渗透率,μm2;
h—油层厚度,cm;
μo、μw—原油、地层水黏度,mPa·s;
Δp—生产压差,10-1MPa;
re—井控半径,cm;
rw—井径,cm;
s—表皮系数,无因次;
Vp—井控范围孔隙体积,cm3;
t—见水后生产时间,s;
a、b—拟合参数,与孔喉分布以及润湿性有关;
水相指数nw、油相指数no是取决于储层岩石孔隙结构和润湿性的2个指数,其变化范围为2~4。
