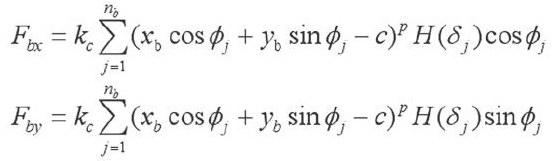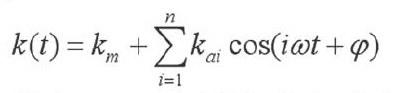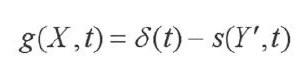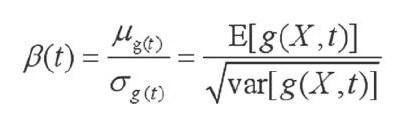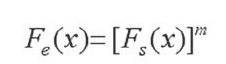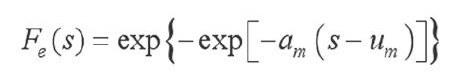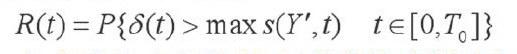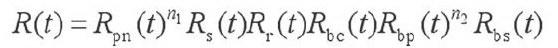随机风载作用下风力发电机齿轮传动系统动态可靠性分析

万晨辉

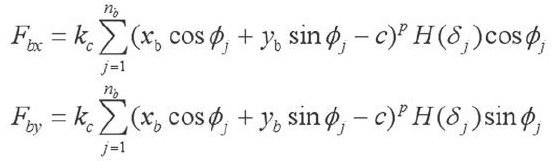
摘要：在风力发电的过程中，风力发电机是不可缺少的重要设备，其可靠性直接关系着风力发电的实际效能。因此如何提高风力发电机的可靠性已经成为当前阶段风电行业发展面临的关键问题之一。本文将通过“齿轮

滚动轴承耦合动力学模型”以及“传动系统动态可靠性模型”的构建探讨随机风载作用下风力发电机齿轮传动系统动态可靠性，希望可以为风机可靠性的提升提供一定的参考。

关键词：随机风载；风力发电机；齿轮传动系统；可靠性

可靠性是产品具有时间属性的质量指标，它体现了产品在规定条件和规定时间下完成规定功能的能力。提升产品的可靠性可以降低故障和事故发生的风险，降低维护成本。目前，可靠性已经成为国内外各研究机构的研究重点。作为风力发电机中连接叶轮和发电机的重要部件，增速箱由于长期处于随机风载环境下，很容易因故障而失效。因此探究其齿轮传动系统动态可靠性具有重要意义。

一、构建齿轮-滚动轴承耦合动力学模型

（一）构建随机风速模型

在风力发电的过程中，风场随机风速的大小及变化对风电齿轮箱工作性能和可靠性有着较大的影响。因此在进行风力发电机齿轮传动系统动态可靠性研究的过程中，有必要建立和实际风速相符合的随机风速模型。具体实施中，首先要进行风速值的实际测定，并对其进行校正和标准化变换，在此基础上采用径向基核函数支撑向量模拟方法对变换后的数值进行分类和学习，通过交叉检验方法选取径向基函数得最佳宽度，固件基于最小二乘支持向量机方法的风力发电机风速预测模型。在进行风力发电机传动系统动力学及动荷载仿真模拟的过程中，需要将该风速模转化为有效的风速时间历程曲线。

（二）滚动轴承动态轴承力

在确定滚动轴承动态轴承力时，我们需要假定滚动轴承内圈和施转轴处于刚性连接状态，其外圈和轴承座呈刚性连接，同时滚动体在内外圈之间等距离排列，且滚动体和滚道之间不存在相对滑动，此时轴承之间的变形主要表现形式为滚动体和滚道之问的接触变形。在此前提下，需要对滚动体中心之问的夹角β、滚动轴承接触角α、滚动体直径Db、滚动体中心直径Dp、滚动轴承初始间隙c、滚动体位置角φ等参数进行测量掌握，最后根据滚动轴承运动学和赫兹接触理论，推导动态轴承力，具体公式如下：

上式中，Xb，Yb分别为内圈中心在x、y两个方向产生的振动位移，n为滚动体个数，K为赫兹接触刚度。

（三）系统内部刚度激励

刚度激励即是指齿轮啮合过程中由啮合综合刚度的时变性引起的动态激励。首先，我们可以利用石川法对各啮合齿轮的变形进行计算，获得单对齿的时变啮合刚度以及双对齿的时变啮合刚度。为了方便计算，可以将轮齿时变拟合刚度的变化近似为矩形方波的周期白哪壶，这样就可以跟库傅里叶级数进行展开，省略高阶项之后可以获得以下公式：

其中，Km为平均啮合刚度，Kai为变刚度幅值系数，ω为轮齿啮合频率，Nm为转速、Z为齿数。

（四）系统外部随机风载激励

根据上文中建立的风速模型對风速引起的时变荷载进行模拟，将其作为系统的外部激励。之后根据空气动力学的理论就可以获得计算公式：

其中P为叶轮的输出功率，ρ为空气密度，r为叶轮半径，Cp为风能的利用系数。

二、传动系统动态可靠性模型的构建

（一）建立随机过程功能函数

在风力发电机运行的过程中，其传动系统各零部件受动荷载随时间得变化对可靠性的影响无法忽视，故采用随机过程模拟各零部件的强度以及应力，具体功能函数如下：

其中δ（t）为零部件材料强度退化时的随机变量、s（t）为构建荷载作用效应的随机过程、Y”为与荷载作用效应有关的随机变量。结合一次二阶矩方法和摄动法，可以获得功能函数的动态可靠性指标计算公式：

在上式中，μ为功能函数的均值，σ为功能函数的标准差。

功能函数的动态可靠性计算公式如下：

上式即代表了零部件在其设计服役期间不同时刻t的强度都超过荷载作用时零件才能处于可靠状态下的概率。

（二）载荷随着时间变化的模型

在随机风载作用下，风力发电机齿轮传动系统中的各部件所有的荷载虽然都会随着时间产生变化，但并不服从统一具体的分布规律，因此我们只能利用随机过程概率模型对其进行描述。首先，我们要在一定假设条件下，通过统计分析掌握随时间变化的载荷随机过程的等效载荷概率分布函数，在此基础上获得该载荷随机过程作用下系统的可靠度。

在具体操作中，将设计基准期L内最大荷载随机变量S作为荷载随机过程s（t）的等效荷载，这样就可以推导出概率分布函数：

之后，假设某一时刻荷载随机变量s的概率分布Fs（x）服从正态分布N（μ，σ），则可以根据渐进分布理论获得随机变量最大值的分布函数：

如此就可以获得随时间变化的载荷随机过程等效载荷的分布函数，在此函数下系统可靠度的计算公式如下：

上式即代表着构件在设计基准期内任意时段强度大于荷载效应的概率。

（三）传动系统的动态可靠度

风力发电机传动系统可靠度的计算主要受到齿轮和轴承关键零件的影响，因此，综合以上所有内容，可以推导出系统可靠度的计算公式为：

上式中，R（1）、R（t）、R（t）、R（t）、R（t）、R（t）分别代表着行星轮可靠度、太阳轮可靠度、内齿圈可靠度、行星架支承轴承可靠度、行星轮支承轴承可靠度、太阳轮支承轴承可靠度。

三、结语

综上所述，通过模拟真实荷载建立随机风载作用下风力发电机行星齿轮传动系统平移扭转耦合动力学模型，并应用应力强度干涉模型建立考虑系统齿轮和轴承荷载随时间变化的动态可靠性模型，可以对传动系统及其零部件的动态可靠度进行计算。