基于PLS法岩体边坡抗剪参数确定及稳定性分析

2018-09-10罗昌民周玉新

金属矿山 2018年8期

张默罗昌民周玉新邱宇

（1.中钢集团马鞍山矿山研究院有限公司，安徽马鞍山243000；2.金属矿山安全与健康国家重点实验室，安徽马鞍山243000；3.重钢西昌矿业有限公司，四川西昌615041）

在岩土工程领域，岩体力学参数取值的准确性，关乎整个岩土工程分析的重点，其中对于露天采场岩体边坡的稳定性至关重要。露天矿采场边坡总高度一般都超过百米，整体边坡角每提高一度，所带来的经济价值都是上百万及千万元的效益。因此评价整体边坡的稳定性所需要的岩体力学参数要尽可能接近实际值，才能保证边坡的安全储备，发挥整个矿山的经济价值。

岩体力学参数不仅要进行室内外试验，而且要结合分析的内容，进行定性分析和定量分析相结合，综合考虑众多因素，进而确定反映实际状况的力学参数。在获取岩体力学参数较准确的方法中，现场足尺度原位试验较符合实际状态，但由于这项试验需要时间长、经费高、且受岩体天然结构面、节理面和裂隙水等因素影响，因此宏观岩体力学参数的获取就比较困难，一直都受到一定程度的限制［1］。根据样本数据统计方法，拟合回归确定岩体力学参数时，普通的最小二乘（PL）法回归求解时，常因数据样本多而导致自变量和因变量出现多重共线性问题，使得参数不能稳定有效反映自变量和因变量的关系。对于偏最小二乘（PLS）法，可以将自变量和因变量的高维数据空间投影到相应的低维特征空间，分别得到自变量和因变量相互正交的特征向量，再建立自变量和因变量特征向量间的一元线性回归关系［2］。PLS法将多元回归问题转化为若干一元回归问题，相比于PL法，能够更好地适用于样本数较少而因变量数较多的参数回归分析［3］。因此PLS法可以作为岩体力学参数拟合的一种有效方法。

1 偏最小二乘（PLS）法岩体参数确定

1.1 PLS法建模的准则函数

首先，进行因变量集合Y与自变量集合X数据的标准化处理。X经标准化处理后的数据矩阵记为E0=（E01，E02，……，E0p）n×p，若Y为单因变量问题，则Y经过标准化的数据矩阵为F0=（F01，F02，……，F0p）n×p。记t1是E0的第一个成分，则t1=E0w1，w1是E0的第一个轴，是单位向量，即‖‖w1=1；记u1是F0的第一个成分，则u1=F0c1，c1是F0的第一个轴，并且‖‖c1=1。若要t1、u1能很好地代表X和Y中数据的变异信息，根据主成分分析原理，则有：

由于回归建模的需要，t1要对F0有最大的解释能力，由典型相关分析思路，即要求t1与F0的相关度达到最大：r(t1,u1)→max；也要求t1与F0的协方差达到最大：

正规的数学表达是求解下列最优化问题：

1.2 基于拉格朗日算法的极大值求解

若采用拉格朗日算法，记：

对L分别求关于w1,c1,η1,η2的偏导数，并令之为零得：

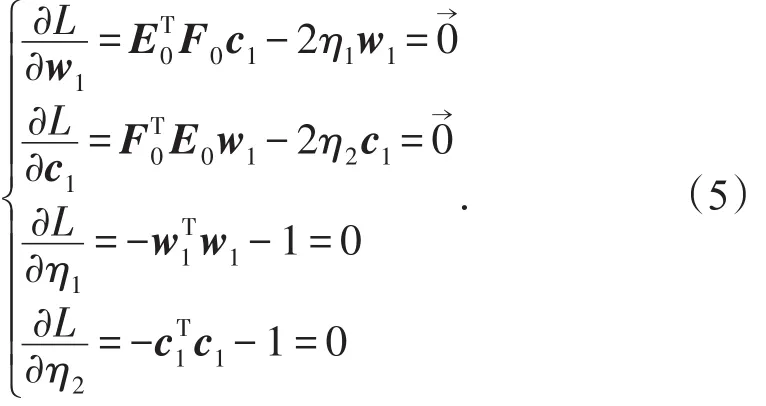
可见，w1与c1分别大特征值η2所对应的特征向量。

1.3 降维空间权值向量w1和c1的提取

1.4 回归方程的建立

求得 w1与 c1和成分 t1和 u1后，分别求E0和F0对t1的2个回归方程：

E1、F1分别是式（8）回归方程的残差矩阵。用残差矩阵 E1、F1分取代 E0、F0，求第二个轴 w2和 c2以及第二个成分t2和u2，如此计算下去，若X的秩为A，则有：

根据所提取的m个成分t1,t2,…,tm，实施F0在t1,t2,…,tm上的回归，直到被提取的残余矩阵达到满足的精度要求为止，精度可通过交叉性检验判别。最后可以得到模型：

最后将t1,t2,…,tm还原成原变量 x1,x2,…,xm的回归方程。

1.5 交叉有效性检验

进行交叉有效性检验，用式（11）检验。若满足条件，只提取一个成分，否则用E1、F1代替 E0、F0，重复上述步骤，直至≤0.097 5，停止计算。

式中，PRESSh为因变量拟合误差平方和；SSh-1为样本点拟合（h-1）个成分的方程的拟合误差。

2 旺儿沟采场北帮岩体边坡参数确定

独山城矿区旺儿沟采场北帮出露地层较简单，主要为震旦系辉长岩，由于接触交代变质和风化蚀变作用，形成较破碎的辉长岩。蚀变辉长岩为矿区的主体岩性。北帮较破碎的辉长岩因受强发育节理裂隙影响，上部北帮边坡连续出现了3～6个台阶的整体连续滑塌破坏，并逐渐会变为较深层次的滑塌。在经过现场地质调查和室内试验，也难较准确地得出强风化辉长岩的综合岩体强度参数。在此以抗剪强度参数c、f为双因变量，考虑岩石的点荷载强度I、孔隙率n、天然密度 ρ为影响因素，进行PLS法回归拟合强风化辉长岩的强度参数，进而进行边坡的稳定性分析。

对现场不同台阶边坡采集了11组样本，进行了点荷载强度、孔隙率和天然密度实验，试验数据见表1所示，表中c和f值为原勘察试验值［4］。

各变量之间的相关系数［5］按照式（12）计算，计算结果为式（13）。其中Cov(x,y)为x与y的协方差，Var(x)和Var(y)为x和y的方差，当相关系数为负时，表示随自变量增加而减小的负相关。相关程度一般用绝对值大小判断，绝对值越接近1，表明和自变量越相关。经过计算各变量之间相关系数存在多重共线相关性。采用其他回归分析，会造成结果与实际值相差甚远，因而采用PLS法回归分析较为合理，可以建立统计计算方程为

对因变量和自变量进行标准化处理，再利用PLS法进行回归提起有效成分，并作交叉有效检验，结果见表2所示。

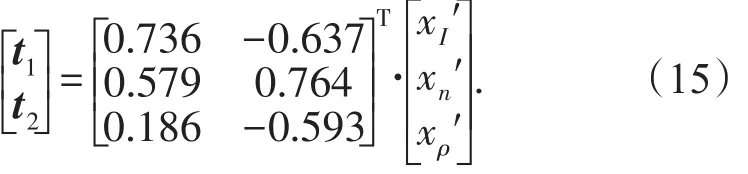
实施［c，f］在t1和t2上的线性组合为式（16），拟合值见表3所示，最终提出边坡稳定性计算的综合抗剪强度参数推荐值。

3 旺儿沟采场北帮边坡稳定性分析

通过PLS法确定的岩体抗剪强度参数，用于边坡稳定性分析，与勘察试验强度参数值所计算的稳定性进行比较，进而反映边坡实际破坏的安全状态。

经过现场边坡调查定性分析，旺儿沟采场北帮边坡主要为强风化辉长岩，采用弹塑性强度准则的应力—应变机理作为岩体边坡的破坏准则较为合理。数学形式采用有限差分法，从而得到边坡的临界剪应力作为失稳的判据。边坡安全系数采用岩体实际抗剪强度与临界破坏时的剪切强度的比值定义安全系数，即强度折减法［6］。边坡整体弹塑性应力—应变和安全系数计算采用目前较为成熟的FLAC3D软件。

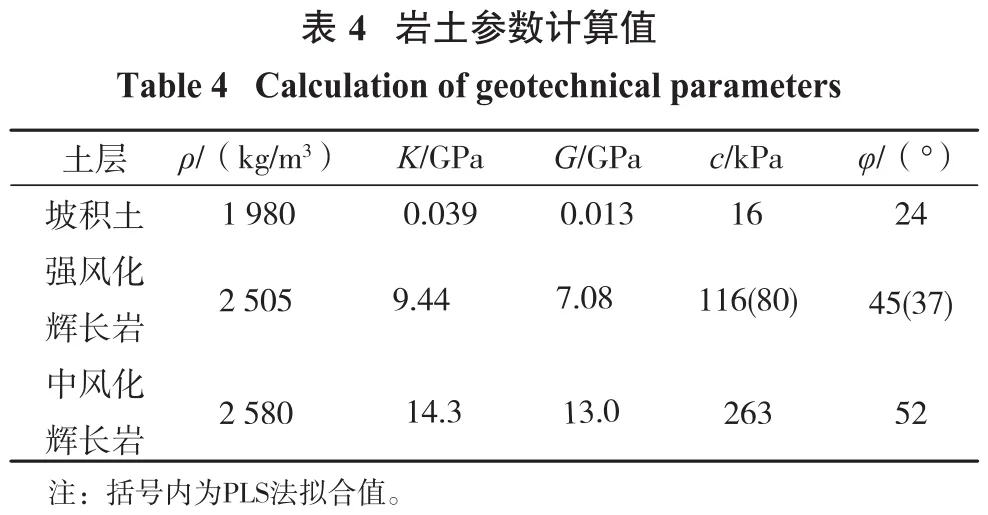
通过PLS法确定的岩体参数和勘察试验参数见表4，现场边坡见图1，三维地质模型见图2，不同参数计算的临界剪力及安全系数见图3和图4。

通过边坡稳定性计算得到的由勘察报告提供的岩体抗剪强度参数计算的剪切破裂面仅局限在上部的坡积土（图3）。但从边坡现场踏勘情况可以看出，已经出现连续3～6个台阶的整体连续滑塌破坏，而由PLS法确定抗剪强度参数计算的剪切破裂面分布于强风化辉长岩边坡上（图4），破裂面很符合现场滑塌情况。前者计算的安全系数为1.455也远大于后者计算的安全系数1.162。因此，不管从剪切破裂面分布特征，还是安全系数大小，PLS法确定的岩体抗剪参数较贴切实际岩体边坡的抗剪强度参数。