钢支撑伺服系统在轨道交通工程中的应用

吉茂杰

上海申通地铁集团有限公司 上海 201101

1 工程概况

上海轨道交通14号线浦东大道站与已运营的4号线浦东大道站“十”字换乘。车站被4号线大连路隧道、4号线浦东大道站车站分为3个基坑。西区基坑的标准段宽度为24.65 m，围护采用厚1 m、深50 m地下连续墙，沿基坑深度共设置6道支撑，第1道和第4道为混凝土支撑，第5道为φ800 mm钢支撑，其余为φ609 mm钢支撑。车站周边环境复杂，车站西南侧的崂山一村距离车站仅约6 m。基坑①～⑤轴之间所有钢支撑均采用轴力伺服系统，⑤～ 轴之间部分钢支撑采用轴力伺服系统（图1、图2）。

第3道钢支撑（普通或伺服）标高为－9.10 m，第4道混凝土支撑标高为－12.30 m，第5道伺服钢支撑标高为－16.50 m。

2 伺服钢支撑工作原理

普通钢支撑预加轴力后在其活络端打入钢楔块以锁定轴力，锁定过程中由于钢楔块的变形会带来瞬间的轴力损失，并且钢支撑在受地下连续墙挤压后会产生弹性压缩，不能自动调整钢支撑的轴力和长度，只能被动受压。

图1 基坑支撑布置平面

图2 基坑支撑布置剖面

伺服钢支撑是将普通钢支撑的活络端替换为专用支撑头，支撑头内部设千斤顶，可以智能地根据设定的程序进行钢支撑轴力和位移的调控[1]。在地下连续墙变形向内挤压钢支撑使其缩短的同时，支撑头会主动调整千斤顶的油缸，使油缸产生向外的行程，弥补钢支撑的压缩量，从而控制了地下连续墙的变形。位于支撑头上部的超声波测距传感器可以测量内置千斤顶油缸的行程，该行程将用于支撑轴力的控制与基坑变形数据分析（图3）。

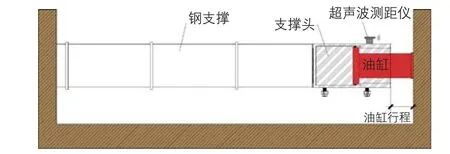
图3 伺服钢支撑的工作示意

3 钢支撑变形的实测数据分析

本节将对全伺服区域的P2和P35测斜孔，部分伺服区域的P3和P34测斜孔进行分析，全伺服区域的钢支撑均为伺服钢支撑，部分伺服区域的第2道和第3道钢支撑为普通钢支撑，第5道和第6道钢支撑为伺服钢支撑。各测斜孔对应的支撑编号及安装日期如表1所示。

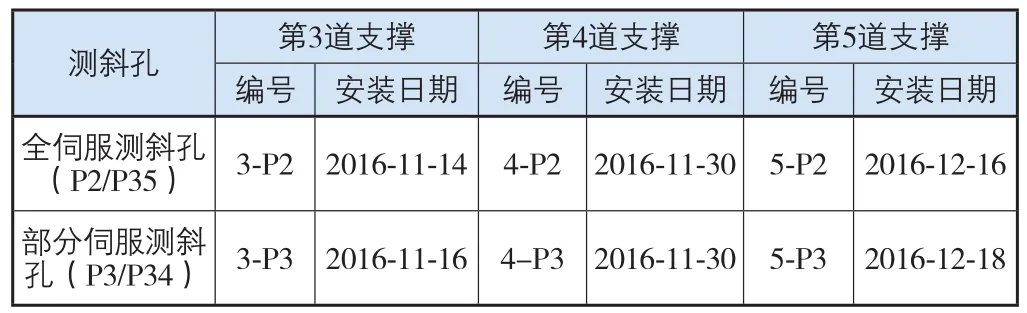
表1 各测斜孔对应的钢支撑编号及安装日期

下面分析第3道钢支撑分别采用伺服和非伺服方式的位移控制效果。第3道钢支撑的轴力随着基坑的下挖不断增大，按第3、4、5道支撑安装的时刻分为3个开挖节点进行分析，第3道钢支撑在各开挖节点的轴力分别列入表2。

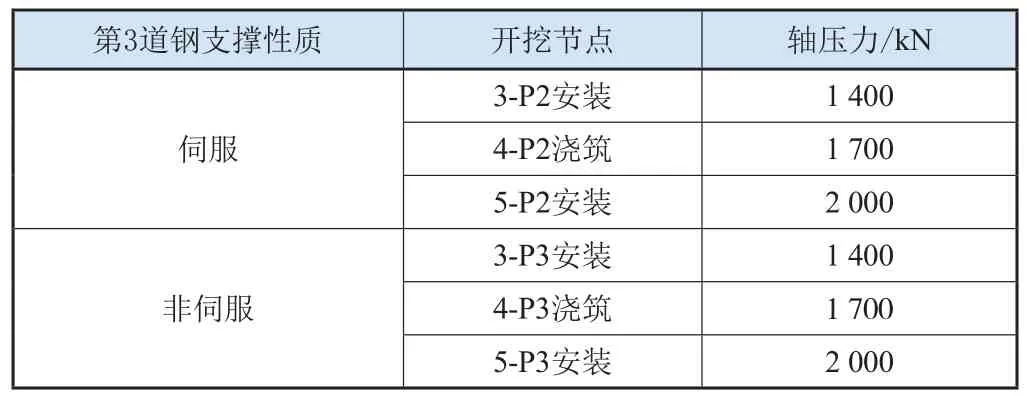
表2 第3道钢支撑在各开挖节点的轴力

根据现场测斜数据，可得到测斜孔的位移曲线（图4、图5）。

从图4可以看出，全伺服区域的第3、5道伺服钢支撑安装好以后，各标高位移曲线会有减小趋势，随后很长一段时间都缓慢发展，而第4道混凝土支撑并不能带来位移的稳定。测斜孔P2及P35所对应的第3道支撑标高（－9.10 m）处的地下连续墙变形值记为sp2和sp35。

图4 P2/P35测斜孔对应各开挖节点的地下连续墙位移曲线

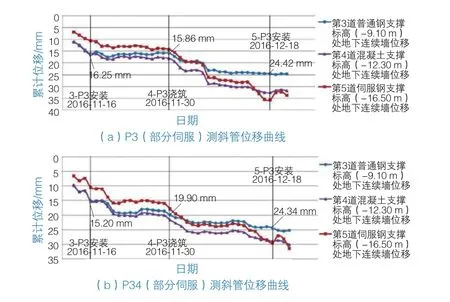
图5 P3/P34测斜孔对应各开挖节点的地下连续墙位移曲线

从图5可以看出，在第3道普通钢支撑3-P3安装好以后，－9.10 m标高处的位移仍在缓慢增大，在第4道混凝土支撑4-P3浇筑好以后该标高处位移继续增大，直到第5道伺服钢支撑5-P3安装好以后，该标高的位移发展趋于平缓。从－16.50 m处地下连续墙的位移曲线可以看出，在5-P3伺服钢支撑安装好以后，该标高的位移有向基坑外侧变形的趋势，之后位移发展趋于平缓。将测斜孔P3及P34对应的第3道支撑标高（－9.10 m）处的地下连续墙变形值记为sp3和sp34。

我们从以上测斜曲线中的数据分析第3道钢支撑标高位置（－9.10 m）的双侧地下连续墙收敛值。由于测斜孔P2对应的基坑另一侧测斜孔位为P35，测斜孔P3对应的基坑另一侧测斜孔位为P34，因此将相对应的2个测斜孔位的变形值叠加，就是第3道钢支撑标高位置的双侧地下连续墙收敛值，即钢支撑的实际压缩值lac，5-P2（5-P3）安装时刻与3-P2（3-P3）安装时刻的钢支撑压缩值之差为Δlac（表3）。

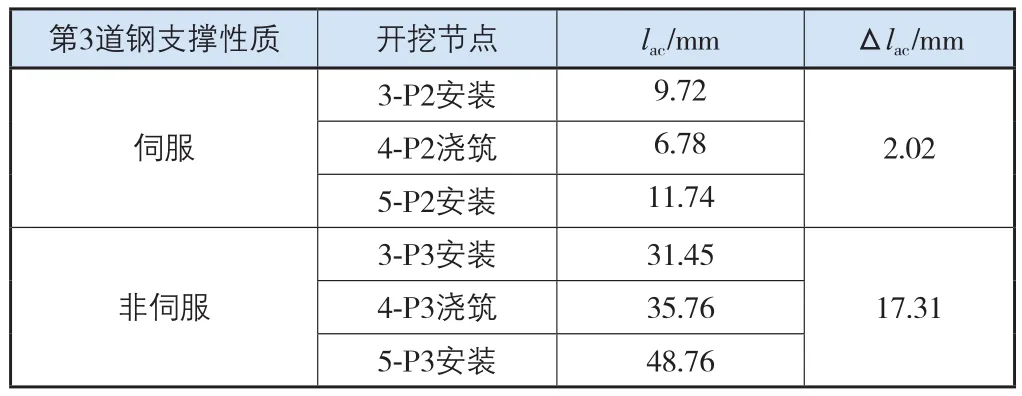
表3 第3道钢支撑在各开挖节点的实际压缩值

第3道伺服钢支撑实际压缩值：lac=sp2＋sp35。

第3道非伺服钢支撑实际压缩值：lac=sp3＋sp34。

第3道支撑分别采用伺服和非伺服钢支撑，当轴力大小相等时，基坑水平位移却相差很大，即钢支撑的总压缩量相差很大。且从3-P2（3-P3）安装时刻到5-P2（5-P3）安装时刻这段时间，伺服钢支撑产生的位移增量只有2.02 mm，而非伺服钢支撑却达到了17.31 mm。

4 钢支撑变形的理论计算分析

本节将通过理论分析，探究基坑变形的组成，从而解释伺服钢支撑变形较小的原因。

4.1 钢支撑在轴压力作用下的变形

第3道钢支撑均为φ609 mm钢支撑，外径D=609 mm，壁厚t=16 mm，钢支撑长度L=24 m，钢材弹性模量为E=210×103MPa。经计算，φ609 mm钢支撑的受力面积A=29 792 mm2，则钢支撑在轴压力作用下的压缩值lF=F·L/（A·E）。根据此式，可得到第3道钢支撑在各开挖节点轴压力作用下的压缩值。

4.2 钢支撑在温度作用下的变形

钢支撑长24 m，线膨胀系数为12×10-6K-1，该工程施工期间最大温差为15 K，因此该钢支撑热胀冷缩的最大变形值[2]为：lt=4.32 mm。

4.3 钢支撑在工作状态下的理论最大压缩值

钢支撑在预加轴力作用下会产生初始压缩变形，之后开始工作，在土压力作用下，钢支撑轴压力增大时变形也相应增加，各轴压力增量ΔlF和温度作用下的变形lt之和即为它的理论变形值lth。因此：lth=ΔlF＋lt。

轴压力为1 400 kN时，发生初始压缩变形lF=5.37 mm，ΔlF=0 mm；轴压力为1 700 kN时，钢支撑压缩值lF=6.52 mm，ΔlF=6.52－5.37=1.15 mm；轴压力为2 000 kN时，钢支撑压缩值lF=7.67 mm，ΔlF=7.67－5.37=2.30 mm。

综上所述，不同轴力作用下钢支撑的理论最大压缩值如表4所示。

对比表3中的钢支撑实际压缩值和表4中的钢支撑理论压缩值发现，伺服钢支撑的实际与理论压缩值相差不大，而非伺服钢支撑的实际压缩值远远大于其理论压缩值。

轴力伺服系统的特点在于它可以通过自动调节油缸长度来弥补钢支撑的压缩量，主动控制地下连续墙的位移；而普通钢支撑由于无法自动调节自身长度，因此在地下连续墙的压力作用下，节点之间的压缩及挠曲变形使钢支撑产生了很大的压缩，从而带来了更大的地下连续墙位移。表3中伺服钢支撑与非伺服钢支撑的位移控制效果相差悬殊，在于伺服钢支撑主动调整自身长度弥补了钢支撑在挠曲变形及节点压缩过程中所产生的变形。因此，使用伺服段的变形远小于非伺服段的变形，该变形差将在下节中得到数据证明。

表4 不同轴力作用下钢支撑的理论最大压缩值

5 伺服钢支撑的变形分析

支撑轴力伺服系统的位移测量功能是通过测量支撑头内千斤顶的行程来实现的[3]，超声波测距仪是目前比较先进的一种位移测量方式，此次工程采用的支撑轴力伺服系统即使用超声波测距仪进行位移测量。P2测斜管对应的第3道伺服钢支撑为3-P2，在3-P2安装当日（11月14日）和5-P2安装当日（12月16日）的平均轴力及平均油缸行程见表5。从支撑轴力伺服系统的数据平台上可得到轴力-油缸行程/时间曲线（图6）。

表5 伺服钢支撑3-P2轴力与油缸行程

图6 伺服钢支撑3-P2轴力-油缸行程/时间曲线

根据上述数据分析，轴力由1 400 kN增加到2 000 kN时，钢支撑的实际压缩值、理论压缩值和油缸行程的情况如表6所示。表中的Δl表示3-P2安装时刻至5-P2安装时刻间所产生的位移增量。

由表6可知，从3-P2安装时刻至5-P2安装时刻，伺服钢支撑的实际压缩值与油缸行程之和为2.02＋14.16=16.18 mm，接近于非伺服钢支撑的实际压缩值17.31 mm。再次表明了伺服系统可以通过主动调整钢支撑的长度，很大程度地补偿其在压力、温度及节点拼接间隙等各种因素下的压缩量。即：

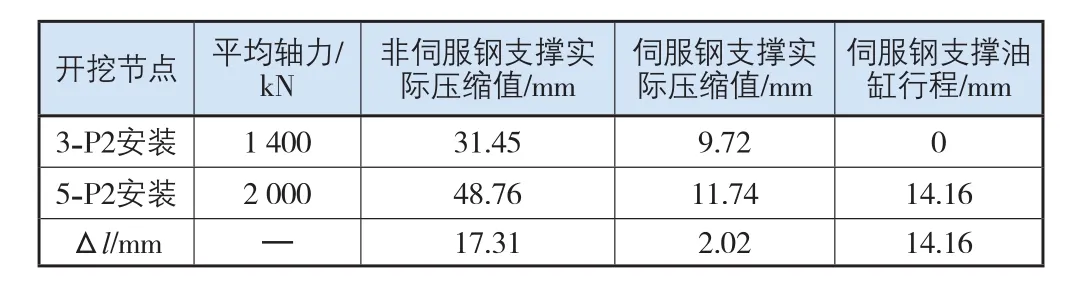
表6 3道钢支撑标高处地下连续墙的位移增量

正是由于该恒等式的存在，轴力伺服钢支撑大大限制了地下连续墙位移的产生。

6 结语

本文结合上海轨交14号线浦东大道站的工程案例，对比了普通支撑与伺服支撑的变形控制数据。通过理论计算与实测数据分析，证明了伺服钢支撑实际上是一种可以智能伸缩的钢支撑，千斤顶的伸出量有效地补偿了支撑挠曲变形及节点拼接处的变形，并且在一定程度上补偿了温度及土压力变化带来的支撑本体压缩，进一步证明了轴力伺服钢支撑在变形控制方面的有效性，可为进一步优化支撑轴力伺服系统的控制算法提供理论依据[4-5]。