一种改进的跳频信号时频分析方法
2018-09-10冯维婷
冯维婷, 梁 青, 谷 静
(西安邮电大学 电子工程学院, 陕西 西安 710121)
跳频信号是一种分段平稳信号,广泛应用于雷达和通信领域[1-2]。时频分析可以得出跳频信号的特性[3-4],揭示信号频率随时间变化情况。时频分析分两类,一类是以短时傅里叶变换(short time Fourier transform, STFT)、平滑伪魏格纳分布(smoothed pseudo wigner-ville distribution, SPWVD)为代表的非参数化时频分析方法。其中,STFT是线性变换,不存在交叉干扰项,但受测不准原理的制约,时间和频率分辨率不能同时兼顾[5-6];SPWVD是非线性变换,时间和频率分辨率高,但存在交叉干扰项,需要通过设计核函数抑制交叉干扰项[7-8]。另一类是以时变自回归(time-varing auto regressive, TVAR)模型为代表的参数化时频分析方法[9-10],适合描述瞬时频率连续变化信号,可获得较高时间和频率分辨率,而跳频信号的瞬时频率是有间断点的分段连续,故其并不适合跳频信号分析。
稀疏表示理论应用广泛[11-12],可以考虑采用稀疏表示算法对跳频信号进行时频分析。跳频信号在频域具有稀疏特性,可以在频域构造傅里叶基矩阵,通过迭代寻求稀疏向量对应的傅里叶基,从而根据稀疏向量获得信号稀疏度,并估计跳频信号的各频率分量。但是,为了提高估计精度时,傅里叶基矩阵的长度会相应增大,算法的计算量会急剧增大。
本文将结合跳频信号瞬时频率分段连续的特点,将接收信号分成若干小段,对每段信号利用FFT获得频率预估计值和信号稀疏度,再利用预估计值构造频率细化的子傅里叶基矩阵,建立分段信号的稀疏表示模型,最后,基于正交匹配追踪算法(orthogonal matching pursuit, OMP)[13-14]获得高精度的时频谱图。
1 跳频信号的稀疏表示模型
假设观测信号模型为
(1)
其中t∈[0,T],w(t)是观测噪声,si(t)是第i分量跳频信号,且
fk为观测时间段内的第k个跳频频率;M为频率跳变个数;rectTh(·)是持续时间为Th的窗函数。
对观测信号采样,把采样数据等间隔划分成D段,每一小段数据的持续时间要短于跳频信号的持续周期,每段长度为P点,构造观测矩阵
Y=[y1,y2,…,yD]。
(2)
其中
yi=[y(i-1)P,y(i-1)P+1,…,yiP-1]T
为观测矩阵的第i列向量(i=1,2,…,D)。
建立傅里叶基矩阵
W=[w0,w1,…,wP-1]。
(3)
其中
为第m个基向量(m=0,1,…,P-1)。
观测信号可以表示为
Y=WX+V。
(4)
其中,Y∈P×D,W∈P×P,X是稀疏矩阵,V为噪声矩阵,X,V∈P×D。X中只有有限个非零值,且对应于跳频信号中有限个跳频频率对应的窄带信号的幅度,故跳频信号可在频域进行稀疏表示。因X是稀疏的,故有稀疏表示模型
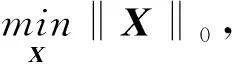
(5)
其中, ‖X‖0为L0范数。L0范数的极小化不能直接求解,需转化为解相同的L1范数求解[15],故将式(5)转变为凸优化问题

(6)
其中,ε为允许误差。
式(6)的求解基于OMP稀疏表示算法。X中非零值元素的个数就是信号的稀疏度,非零值元素的位置就对应各分段窄带信号的频率估计值。假设X的稀疏度为k,OMP算法在傅里叶基矩阵中通过迭代寻求与残差信号相关性最大的傅里叶基向量来匹配出k个稀疏向量。OMP算法中需要预先给出稀疏度k值,但是在实际应用中,多数情况下k值是未知的,若k值设置不合适,算法性能下降甚至失效。另外,时频分析精度取决于算法中傅里叶基矩阵的长度,分析精度越高,傅里叶基矩阵长度越大,则算法运算量也会急剧增大。
2 算法原理及步骤
OMP算法进行稀疏表示时存在两个问题:一是稀疏度设置不合适导致算法性能下降甚至失效;二是傅里叶基矩阵长度太大导致运算量剧增。为了解决这些问题,还需结合频率预估计进行求解。
将跳频信号划分成若干段,对每一小段跳频信号yi进行傅里叶变换,设置能量门限,采用传统谱分析算法估计出信号频率fi(i=1,2,…,k),同时得到稀疏度估计值k。然后根据频率精度要求构造子傅里叶基矩阵:以fi为频率中心,把带宽为Δf的频率段等间隔划分成Q点。
构造出的子傅里叶基矩阵为
将多个子傅里叶基矩阵联成过完备傅里叶基矩阵
D=[D(f1),D(f2),…,D(fk)]。
其中,D的维数为N×kQ。
改进的跳频信号时频分析稀疏表示算法具体步骤如下。
步骤1对观测矩阵Y应用传统谱估计方法估得频率值和稀疏度k,并根据估计出的频率值构建过完备傅里叶基矩阵D。
步骤2设置算法容许误差ε>0,非零元素索引集I=∅,残差矩阵R=Y。其中,I是X中非零元素对应在傅里叶基矩阵中位置的集合。
步骤3当满足条件
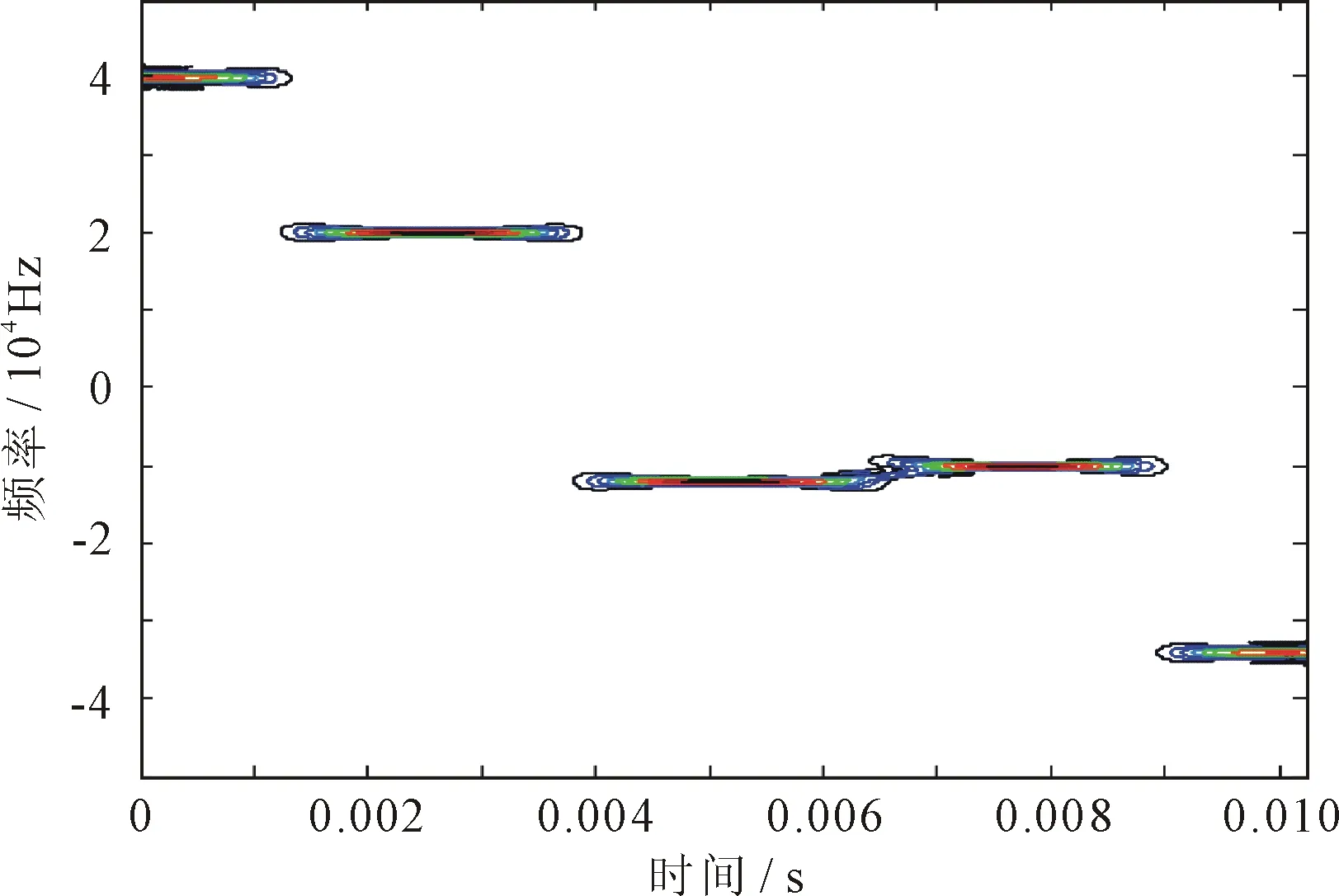
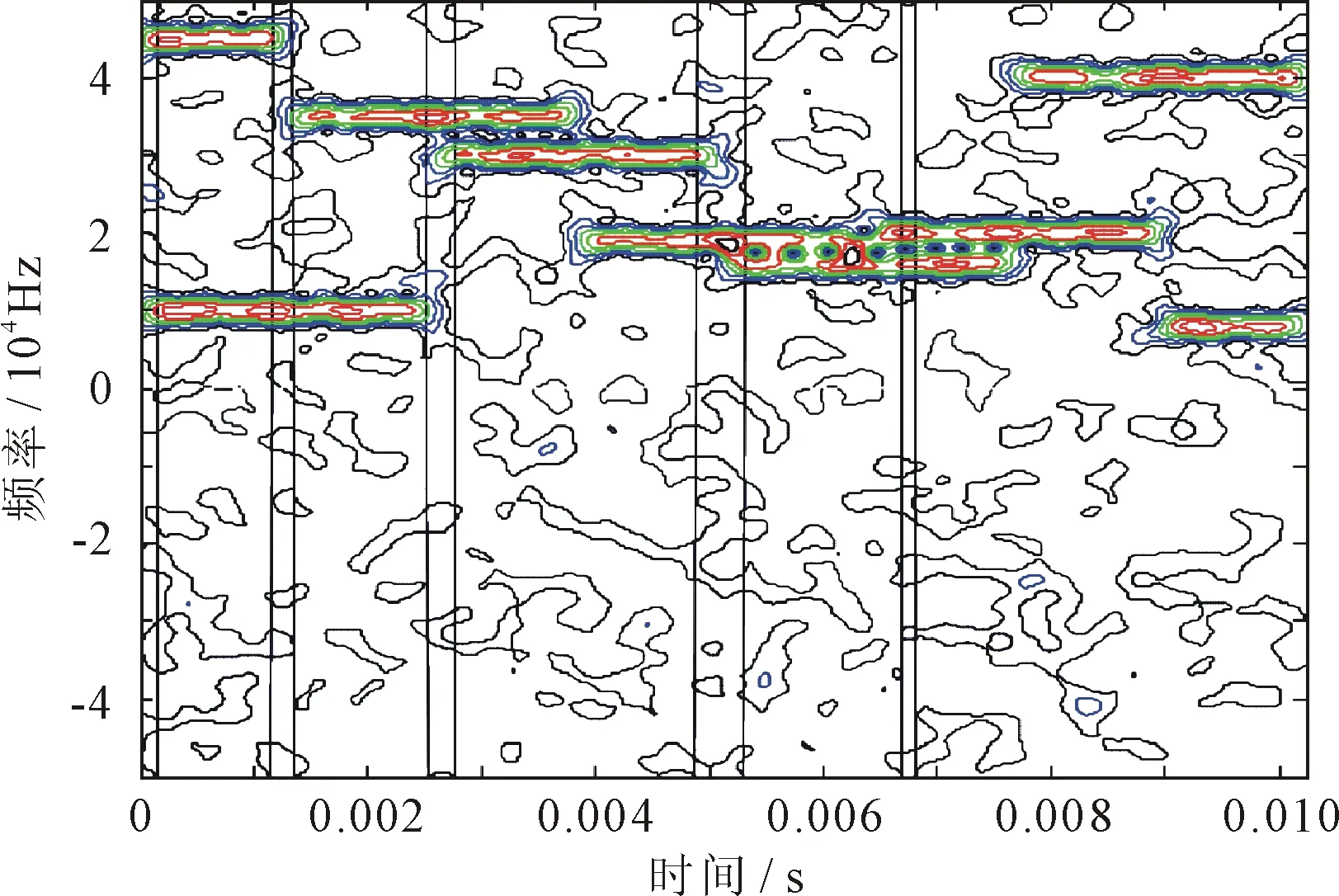
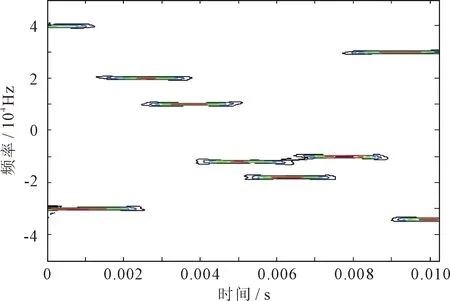
norm(R)>ε&&(n 时,计算残差R与傅里叶基矩阵D中基向量的相关度,取相关度大的前k个;将这k个基向量与能量门限比较,超过能量门限的m(m 更新残差 在相同频率估计精度情况下,对比改进算法与OMP算法的计算量。若傅里叶基矩阵的长度为L,稀疏度是k,则OMP算法的计算量为O(k2L)。可见k一定时,计算量与L成正比。若测频范围为1 GHz,取频率分辨率δf=1 MHz,k=3,直接稀疏表示算法计算量为O(9×103);而采用频率预估计构建傅里叶基矩阵,取频率范围Δf=10 MHz,在达到相同的频率精度情况下,傅里叶基矩阵长度仅为30,稀疏表示运算量为O(2.7×102)。由此可见,在相同频率估计精度情况下,傅里叶基矩阵的长度减小,运算量随之减小。改进算法减小了傅里叶基矩阵的长度而降低了稀疏表示的计算量。 所给算法具有两个特点:预先估计频率点,用其构建频率细化的过完备傅里叶基矩阵,以提高频率估计精度;预先估计稀疏度,避免算法失效。 设置信号采样频率fs=100 kHz;采样点数N=1 024,跳频周期为256个采样点。信号等间隔划分成16段,每段长度为64个采样点。先对每段信号进行频率预估计,再在每个频率点附近选取Δf=10δf范围内等间隔划分,取频率分辨率δf=9 Hz,每个子傅里叶基矩阵的长度等于10。 仿真1选取一段跳频信号,跳频频率依次为45 kHz,35 kHz,19 kHz,20 kHz,8 kHz。第一跳频的持续时间为64个采样点。跳频信号时频谱如图1 所示。 (a) STFT方法时频谱 (b) SPWVD方法时频谱 (c) 预估计的OMP方法时频谱 图1显示了STFT方法、SPWVD方法和基于频率预估计的OMP方法得到的跳频信号时频谱图比较结果。图1(a)显示,时频谱图不能有效区分第三、四跳的频率,这是由于STFT算法所得频率聚集性较差,频率分辨率较低;图1(b)采用平滑伪WVD方法,设计的核函数抑制了交叉项,但也降低了时频分辨率。图1(c)的谱线更细,具有更高频率分辨率,可以区分第三、四跳的频率,这是由于采用频率预估计使得傅里叶基矩阵中频率得以局部细化,频率估计精度相当于在整个频率范围内建立频率间隔为0.009 kHz的过完备傅里叶基矩阵,因此其频率分辨率更高。 分别选取t为0.001 s、0.003 s、0.005 s的时间点,用STFT方法、SPWVD方法和基于频率预估计的OMP方法进行频率估计,并与频率真值对比,结果如表1所示。 表1 单分量信号频率估计值对比表 表1数据表明基于频率预估计的OMP方法所得频率估计精度高于其它两种方法。 仿真2考虑两分量跳频信号的情况。产生第二段跳频信号:第一跳频从0时刻开始起跳,跳频频率依次为10 kHz,30 kHz,16 kHz,40 kHz;产生复高斯白噪声,信噪比为5 dB。两段跳频信号的时频谱如图2所示。 图2(a)中时频谱线受噪声影响较大,图2(b)中两信号各自的跳变时刻频谱线清晰度降低,而图2(c)中跳变时刻频谱线清晰可辨。由此可见,结合频率预估计的OMP方法更适合于多分量跳频信号的时频分析。 综上可知,在STFT方法、SPWVD方法和基于频率预估计的OMP方法中,后者具有更高的时频分辨率和更强的抑制噪声能力。 (a) STFT方法时频谱 (b) SPWVD方法时频谱 (c) 预估计的OMP方法时频谱 通过频率预估计给出了跳频信号的稀疏度和各频率估计值,构造出对应的频率细化的傅里叶基矩阵,得出一种跳频信号时频分析改进的OMP稀疏表示方法。仿真结果验证了改进方法对跳频信号时频分析的有效性。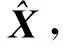



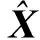
3 仿真实验




4 结语
