RSA算法的改进研究
2018-09-10廖彬宇赖晓风
廖彬宇 赖晓风
摘要:RSA算法具有很好的保密性,在信息安全领域广泛使用,但是算法的运算效率缓慢,在2种提升计算速度算法的基础上提出了RSA综合分解算法。该算法结合了2种算法的优点而产生,性能有进一步的提升。与传统的RSA算法相比,改进的RSA算法在计算速度上有着明显的提升,还拥有良好的可扩展性,因此该算法具有较好的实际意义。
关键词:安全;效率;RSA算法;RSA综合分解算法;提升
中图分类号:TP309文献标志码:A文章编号:1008-1739(2018)14-65-3
Research on Improvement of RSA Algorithm
LIAO Binyu, LAI Xiaofeng
(College of Computer, China West Normal University, NanChong Sichuan 637009, China)
0引言
在现代社会中,由于科学的进步和计算机技术的提升,指数级的信息充斥着我们的周围,信息安全的问题在科学技术发展过程中变得越来越突出,因此信息安全成为了人们非常关注的问题。许多科学家提出了各种各样对网络中信息进行保护的方法,应用最广泛的是由美国MIT的Rivest、Shamir和Adleman在1978年提出来的RSA加密解密算法[1-2],该算法是公钥密码体制中的代表。公钥密码体制是一种非对称的密码体制,算法的加密密钥是公开的,而解密密钥只有信息的接收者知道。RSA算法[3]的安全性是由大整数因子分解的困难程度来保障的,当模数的位数在2 048位时,安全性能够得到很好的保障,但是提升安全性的同时却降低了计算的速度,针对这一问题,本文提出了一种改进方法来提升效率。
1 RSA算法
算法的主要步驟如下:
(1)密钥的产生
选择2个随机大素数和;②然后计算=×,( )=( -1)( -1);③接着随机选择一个整数,满足gcd(,( ))=1;④其次利用欧几里得扩展算法来计算关于模的乘法逆元,即≡1 mod(( ));⑤最后公开、作为加密密钥,保密、、、( ),将、作为解密密钥。
(2)加密算法
(3)解密算法
经过加密算法得到了密文,然后利用解密密钥(,)计算得到明文=mod。
2 RSA算法的改进基础

2.1模数的多次分解算法
多次分解RSA算法定义如下[6]:
①随机选个素数1,2,…,;
②计算=1*2*…*,( )=(1-1)*(2-1)*…*( -1);
③随机选择整数满足gcd (,( ))=1;
④计算,使满足≡1 mod (( ));
⑤公开{,}作为加密密钥,保密1,2,…,,( ),解密密钥为{,};
⑥加密算法:=mod,解密算法:=mod。
2.2负载均衡算法
为了改进大整数幂乘,在文献[7]中提出了明文大整数分解的方法,该方法思想如下,这里以加密算法进行说明。
①设明文可以分解为多个小整数1,2,…,的乘积,即=1×2×…×,那么加密算法就变为= (1×2×…×) (mod ),进一步变形为=1e
2e…(mod )。
②从式子中可以看出1,2…相互之间没有联系,是独立的存在,凭借这一特点,可以将每一部分逐个分配到计算进程中。
③假设明文分解为9个子明文(1,…,9),现有3个进程(1,2,3)。进程1进行1、2、3的幂乘运算,2进行4,
5和6的幂乘运算,按顺序分配,3则进行7、8和9的幂乘运算。
④但是这里存在一个问题,分解后的各个整数大小是不一样的,有较大的整数,也有较小的整数。如果较小的整数分配在同一个进程中,较大的整数分配在同一个进程中,导致分配了较小整数的进程较早完成任务,分配了较大整数的进程较晚完成任务。然而最终的乘积运算需要等到所有的进程任务完成后才能进行,所以会导致某些进程提前完成任务后进行等待,额外地增加等待时间。因此负载均衡算法就是让每个进程的任务分配更加合理,尽可能任务大小一致。
3 RSA综合分解算法
由于模数是一个大整数,那么在密钥生成阶段利用来求解加密密钥和解密密钥的计算速度是低效的。此外如果在加密运算当中的明文也是一个庞大的整数,那么算法的加密运算就是关于大整数的幂乘,同样解密运算也是关于大整数的幂乘,这样就会导致幂乘运算异常的复杂,并且计算速度非常的缓慢。
因此在模数的多次分解算法和负载均衡算法的基础上,提出RSA综合分解算法。通过对RSA算法的了解,算法过程可以大致分为密钥生成及加密和解密2个阶段。
①密钥生成:要完成信息的保密工作,必须先要有密钥,如果能提升密钥生成速度,则可以减少算法执行的时间,而模数的多次分解算法则是在密钥生成阶段进行的改进。
②加密和解密:对明文的加密和对密文的解密是该阶段的主要工作。而负载均衡算法分解明文并尽可能均匀地分配到计算进程中,以此来提升加密和解密速度,缩短计算时间。
RSA算法的运算过程是由密钥生成和加密解密组成,必须首先生成密钥才能进行加密解密,因此算法的2个阶段是递进关系。算法总的执行时间是由2个阶段的运算时间相加而来,即密钥生成的运算时间加上加密解密的运算时间,所以提升2个阶段的运算时间,无疑能有效地提升算法总的执行时间。
因此,基于该思想,把密钥生成阶段的改进和加密解密阶段的改进结合起来生成RSA综合分解算法。以加密过程为例,该算法描述如下:
①随机选个素数1,2,…,;
②计算=1*2*…*,( )=(1-1)*(2-1)*…*( -1);
③随机选择整数满足gcd (,( ))=1;
④计算,使满足≡1 mod (( ));
⑤公开{,}作为加密密钥,保密1,2,…,,( ),解密密钥为{,};
⑥把明文分解成多个小整数,即=1×2×…×,而1,2,…,是素数;
⑦分解之后,对每个小整数进行排序,顺序满足1≤2≤…≤;
⑧排序结束后,对任务进行分配,分配原则:假设有个进程,把1分配给1,2分配给2,3分配给3,即分配给(mod)号进程;
⑨分配完成之后即可以进行幂乘计算了,每个进程各自进行;
⑩在每个进程完成计算任务之后,再进行总的乘积运算,最终完成RSA加密算法的计算。
4 RSA综合分解算法性能分析
模数的多次分解算法是将大整数分解为多个素数相乘,具体的个数可以是任意的,当然分解的个数越多,数值就越小,这样计算机在对这些素数进行运算的时候就可以提高计算速度。此外算法中分解出的多个素数,增加了模数的分解难度,提高了算法的安全性。已通过实验证明当=2 048 bit时,模数的4次分解算法的解密时间是传统RSA算法解密时间的2.69倍,是模数的3次分解算法的1.90倍[6],具体数据如表1所示。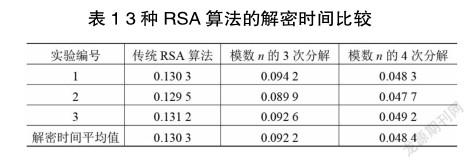
而对于负载均衡算法,原来的明文大整数就变为了多个小整数,计算多个小整数的幂乘所花费的时间比大整数的幂乘明显减小,虽然分解成多个小整数需要花费一些时间,但是与大整数幂乘相比,小巫见大巫。因此借鉴小整数幂乘速度快于大整数幂乘速度的原理,可以得出分解后的幂乘速度有着明显提升,实验数据也表明负载均衡算法对计算效率有着显著的提升[7],具体数据如表2所示。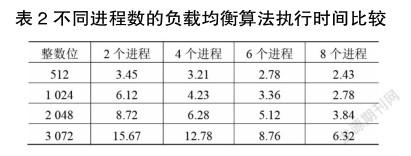
通过表1和表2的数据,可以知道作为密钥生成阶段的模数的多次分解算法比传统RSA算法的计算时间更短,效率更高。作为加密解密阶段的负载均衡算法随着进程的增多而逐渐缩短执行时间。因此得出2个阶段计算效率的共同提升可以进一步提高RSA综合分解算法的运算效率。
5結束语
本文分析说明了模数的多次分解算法和负载均衡算法分别在密钥生成和加密解密阶段对计算效率的提升,在此基础上提出RSA综合分解算法。已通过相关实验数据说明该改进算法在效率上有着进一步的提高,具有一定的实际价值,在未来将继续致力于改进计算速度的研究。
参考文献
[1]陈春玲,齐年强,余瀚.RSA算法的研究和改进[J].计算机技术与发展,2016,26(8):48-51.
[2]陈鹏飞,何小东.RSA算法的分析与改进[J].电子世界,2015(13):111-113.
[3]王树天.RSA算法的改进和实现[J].内蒙古科技与经济,2015(16):93-94.
[4]陈若寒,陈舒.RSA加密算法的研究[J].数字通信世界,2017(10):210.
[5]叶秀芳.RSA算法的优化策略[J].电子设计工程,2017,25(20):83-85,89.
[6]刘平,赵焕平.改进RSA算法的分析研究[J].计算机与现代化,2013(7):84-86,90.
[7]唐笑林.高效RSA算法的研究与并行实现[J].计算机工程, 2013,39(2):164-167,171.
