基于小波Mallat算法的微波信号去噪
2018-09-10胡本钧杨健
胡本钧 杨健

摘要:为准确识别微波信号中的目标信号,文章将小波Mallat算法引入到微波目标信号处理,对微波信号进行分解、重构,去除信号中的噪声,并采用MATLAB软件进行系统仿真,结果表明,用小波Mallat算法对微波信号进行目标识别,可有效的去除噪声,抑制杂波,准确的识别目标信号,具有很好的应用前景。
关键词:小波;Mallat算法;微波
中图分类号:TN974 文献标识码:A 文章编号:2095—6487(2018)02—0084—02
0引言
随着无线通信技术的快速发展,微波逐渐应用到生活的各个方面,它在方便我们生活的同时,也导致微波信号中的干扰越来越严重,微波噪声是复杂的、含有多种成分的一种时域波形,使用传统的傅立叶变换不能很好的去除信号中噪声,识别出目标信号。本文采用小波Mallat算法在多个尺度上对微波信号进行分解,对分解后的信号进行多分辨分析,对其中的高频分量进行阀值处理,对其中的低频部分依次提取其低频系数,从而尽量减少目标信号与噪声在相应坐标系内的重叠,从而实现目标信号与噪声的分离,通过MATLAB软件进行仿真试验,结果表明基于小波Mallat算法对微波信号进行降噪,可以很好的去除噪声。
1降噪过程
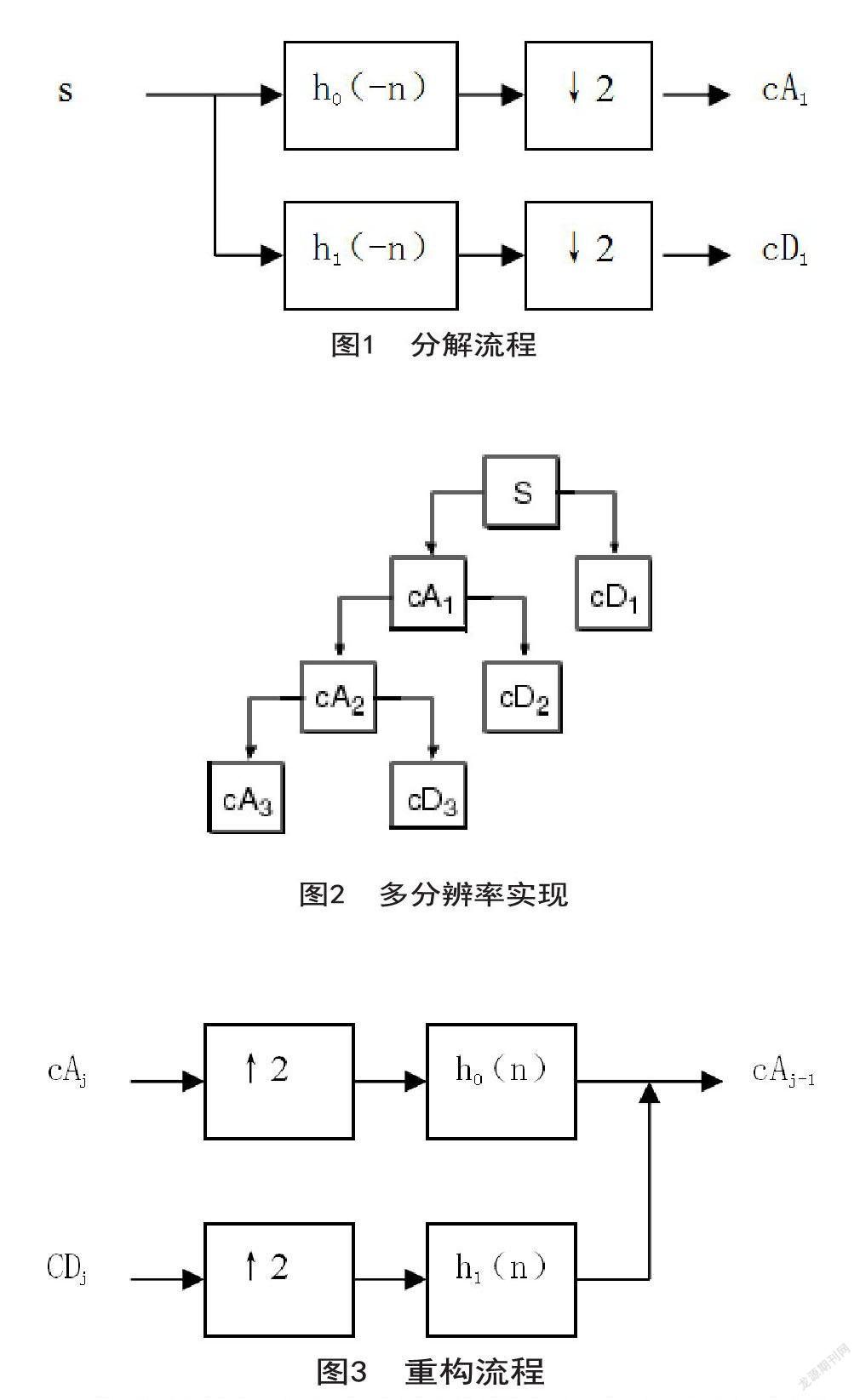
通过选取合适的小波函数,对选定的微波信号通过小波Mallat算法进行J层小波分解。
阀值的选取,即为分解后的各层系数选取阀值,并对各个细节系数做软阀值信号处理,并通过逆小波变换对降噪处理后的系数进行重建,恢复原始信号。
2信号分解
对于原始信号s,其已知长度为N,整个算法最多需要log2N步来完成。
首先,从信号s进行小波分解,对其中的低频部分在原来尺度的1/2尺度上进行小波变换。
能产生两组参数,一组参数是通过作用于低通滤波器能得到一个近似信号,将低通滤波器定义为h0(-n),近似信号定义为cA1,另外一組参数是通过高通滤波器得到细节信号,高通滤波器定义为h1(-n),将细节信号定义为cD1,在这两个信号都是在尺度为2时,滤波器对原始信号进行下采样,图1为算法实现的分解流程图。
其次,采用上面的做法,对分解信号中的低频部分进行再次分解,直到得到所需要的层数为止,图形显示见图2所示,其中cA为低频部分,cD为高频部分。
3信号重构
信号的重构是小波变换的逆运算,它们之间的差异在于,重建过程是先从尺度最低的细节系数cDj和近似系数cAj开始的,通过低频和高频作用,重构出滤波器(h0(n)和h1(n),从而恢复出上一尺度的近似信号cAj-1,然后不断重复上述过程,直到得到原始信号s.
图3为算法实现的单步流程。
将信号分解和重构的过程组合起来就形成了镜像滤波器电路。
4镜像滤波器设计
定义小波基函数如公式(1)所示:
5仿真结果分析
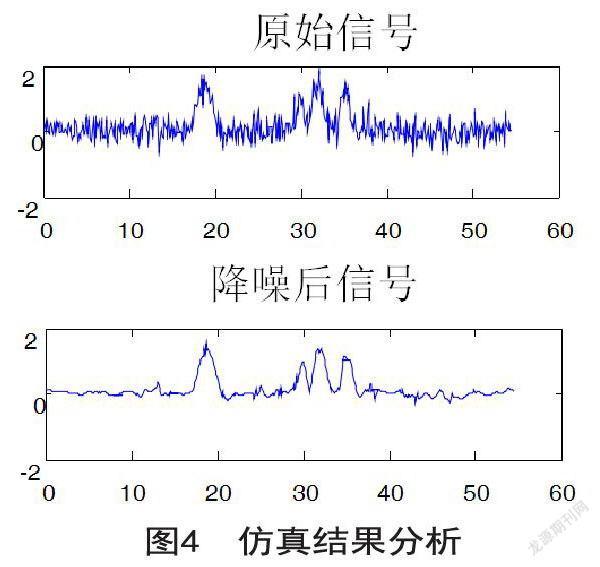
按照上面建立的模型系数对一组受污染的微波信号进行MATLAB仿真。图1中原始信号为受噪声干扰的微波信号。
图4中降噪信号为经过小波Mallat算法重构后的雷达信号与原信号的对比。从图中可以看出重构后的信号与原信号具有良好的相似性与一致性。
通过仿真结果发现,经过小波Mallat算法分解重构后的波形,噪声信号基本被滤除,总体上保持了原信号的特性,达到了很好的滤波效果。
6结束语
文章通过小波Mallat算法对含有噪声的微波信号进行处理,效果优于传统的傅里叶变换。通过MATLAB软件进行仿真实验,结果表明通过小波Mallat算法对微波信号进行降噪,能很好的提取有用信号,具有广阔的应用价值。
