一种基于Logistic混沌方程和ECC的混合加密算法

王尚勇 吴笑峰 胡仕刚 李劲

摘 要：互联网时代的到来给现代科学技术的发展带来了日新月异的变化，尤其是当下比较火热的大数据与区块链技术，更是突出了信息安全以及数据加密的重要作用。本文在对比Logistic混沌映射与ECC的特点的基础上，将两者的优点糅合，去粗取精，提出了基于Logistic混沌方程和ECC的混合加密算法。该算法以Logistic混沌映射的初始参数作为ECC的密钥，来加强加密效率和安全性能。实验结果表明，该算法安全性能极高。

关键词：Logistic混沌映射；ECC；混合加密算法；密钥

中图分类号：TP309.7 文献标识码：A 文章编号：2096-4706（2018）02-0103-03

A Hybrid Encryption Algorithm Based on Logistic Chaotic Equation and ECC

WANG Shangyong，WU Xiaofeng，HU Shigang，LI Jin

（Hunan University of Science and Technology School of Information and Electrical Engineering& Hnust，Xiangtan 411201，China）

Abstract：In recent years，the Internet era has brought new changes to the development of modern science and technology，especially the current hot data and block chain technology，which highlights the importance of information security and data encryption. In contrast to the characteristics of Logistic chaotic map and ECC，this paper will combine the advantages of both，and proposed the hybrid encryption algorithm based on chaotic Logistic equation and ECC. The algorithm uses the initial parameters of the Logistic chaotic map as the key of the ECC，and then strengthens the encryption efficiency and security performance. The experimental results show that the algorithm has high security performance.

Keywords：Logistic chaotic mapping；ECC；mixed encryption algorithm；key

0 引 言

隨着互联网时代的到来，信息化技术也日趋成熟。从对物联网的探索以及大数据、人工智能与区块链技术的一步步提出、优化到应用来看，信息安全[1]对于当下所有的高新技术都是一个无法避免的问题。同时，如今人们生活的方方面面都离不开网络、离不开信息。以一次普通网购为例，从客户付款到商家出货，这其中包括银行、信用卡公司、购物平台的支付中心在内的所有支付中介都清楚地了解你的一举一动。不论有意还是无意，客户的个人信息已经遭到泄漏，已经严重危害到客户的个人隐私与财产安全。因此，为了强化电子商务中数据信息的保密工作，增加人们对网购中自身信息安全的了解，需要特别设计一种针对电子商务[2]环境的信息加密算法。

由此，本文设计出一种基于Logistic映射和ECC的混合加密算法，由Logistic混沌映射对信息进行明文加密，然后以Logistic混沌映射的初始参数作为ECC的密钥，通过ECC中难以穷举破解的离散对数问题进行二次加密，由此极大地提高了加密的安全性。

1 基础加密算法

1.1 Logistic混沌映射

在20世纪中期，Logistic映射[3]作为一个非线性迭代差分方程，被生态学家用来观察生物种群的变化，后来发现其存在复杂的动力学特性，而且还有非常好的初始值敏感性与非周期性，因而被延伸成一种加密算法，并广泛流传至今。Logistic混沌映射表达式以（1）式实现：

xn+1=μxn（1-xn），xn∈[0，1] （1）

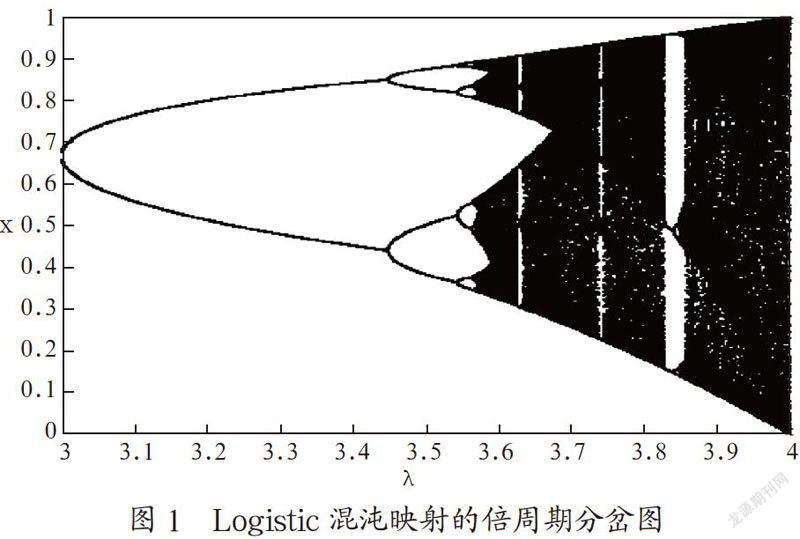
特别地，当μ∈[3.5699456，4]时该混沌映射[4]进入混沌状态，该状态下其值随机地在（0，1）区间浮动（图1）。在μ的值为4时，由（1）式迭代生成的原始序列具有遍历性、随机性等特点。利用Logistic映射具体以下面四个步骤实现加密过程：

（1）选定某个合适的初始值x0；

（2）利用初始值x0对混沌方程xn+1=μxn（1-xn），xn∈[0，1]迭代，生成原始混沌序列L；

（3）对原始混沌序列由加密函数处理得到L′；

（4）将信息明文通过编码转换为0-1序列D，并根据L→L′映射关系对比转换为密文D。

1.2 ECC加密算法

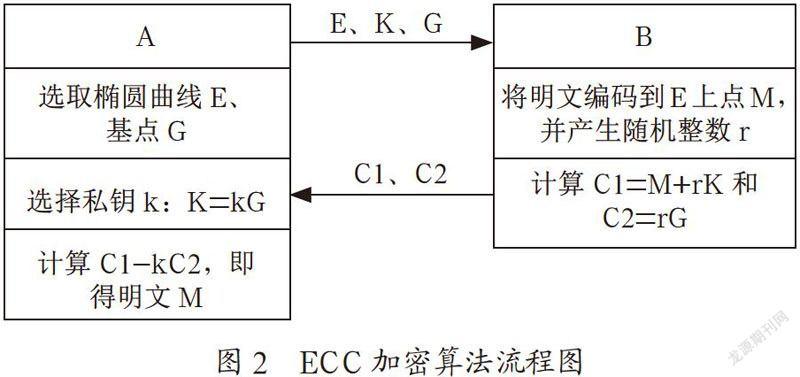
ECC（椭圆曲线加密算法）是以高效性著称的一种基于椭圆曲线理论的非对称公钥加密技术，其加密流程图如图2所示。ECC加密[5]算法采用的是在数学上难以破译的离散对数难题，以如下方式对此问题进行描述：已知大质数p和椭曲E，基于公式Q=KP，给定k、P求出Q相对简单，而给定Q、P求小于p的整数k（k>0）则难以破解。与RSA比较来说，ECC加密在抗攻击性、计算量与存储空间占用方面都具有显而易见的优点，以提供相同的保密程度来说，ECC仅需164位密钥即可，而RSA却需要1024位密钥，这种椭圆曲线[5]上的密码算法在速度和安全性方面也体现出了绝对的优势（见表1）。

ECC加密算法的具体步骤如下：

步骤1：A选定一条椭曲E，并在曲线上取得一任意点作为基点G；

步骤2：A选取私钥k，并由K=kG取得公钥K；

步骤3：A将E和点K、G传给B；

步骤4：B将待发送的明文信息编码到E上的点M，并得到随机数r；

步骤5：B计算点C1=M+rK和C2=rG；

步骤6：B将C1、C2传给A；

步骤7：A收到信息后，计算C1-kC2结果即是点M，因为：

C1-kC2=M+rK-krG=M+rkG-krG=M

步骤8：明文即可被A对M解码获取。

2 基于Logistic混沌映射和ECC的混合加密算法

在Vernam密码体制中，提出了理论上无法破译的“一次一密”密码体制，即对不同的明文采用不同的密钥进行加密。在此情况下，Logistic混沌映射根据其特性可以生成随机原始序列，从而在很大程度上实现了“一次一密”的保密效果。而根据Kerkhoff原理分析，一个加密算法的保密性在于其密钥安全性能的高低，在此情况下，通过利用ECC中难以穷举破解的离散对数问题对其参数进行加密能够保证加密系统的安全性。在混合加密算法中，选取合适的初始值由Logistic方程xn+1=μxn（1-xn），xn∈[0，1]迭代出随机序列对明文进行加密，把Logistic初始值作为ECC明文进行加密生成新的密钥，从而实现加密过程。

3 实验与结果分析

实验是利用电子商务中比较常用的二维码支付进行实验完成的。二维码[6]是一种带有一定规律排列的象形图形，它根据“0”、“1”比特流的概念，可以对数字、文本字符等多种信息进行编码，生成相应的几何形体，再通过光学扫描仪等设备扫描象形图案即可读取信息，其编码过程如图3所示。下面以二维码传输信息为例，加密流程如图4所示，在二维码编码过程中加入混合加密算法，其加密过程通过以下三个模块来实现：

3.1 密文模块

采用Logistic方程对信息明文进行加密。首先小明选取适当的Logistic映射的初始参数，并利用初始参数以及Logistic模型产生原始序列L，对原始序列[7]由小及大排序得到排序后的序列L′，然后小明将信息明文按照编码规则转换成0-1序列DS，并利用L→L′的映射关系对DS进行位置置乱，得到信息密文DS′。

3.2 参数明文加密模块

本模块利用难以破解的ECC把Logistic映射的参数作为密钥进行进一步加密。小密选取适当有限域FP、椭曲E以及点G，选择一个私钥k，利用椭圆曲线算法产生公钥K=kG，然后小密将E和点K、G传给小明。小明将选取的Logistic映射参数（x0，u0）编码到椭圆曲线E上M点，并生成随机整数r，计算点C1=M+rK和C2=rG。

小明对编码C1、C2得0-1CS，然后，小明将CS与上面得到的DS′拼接编码成二维码图片。小密扫描二维码取得C1、C2与信息密文，计算C1-kC2取到M。根据椭圆曲线算法解密M得到参数（x0，u0），再根据Logistic混沌映射借助已经破解的参数将信息密文还原得到原信息明文。

3.3 二维码生成模块

小明将信息密文DS′继续进行一系列的二维码编码操作，并将得到的加密二维码图片发送给小密。

通过上述实验表明，该算法的特点在于安全性能。Logistic混沌映射的随机性以及ECC的离散对数问题的难以破译性使得破译该算法的难度得到指数级的提高。相对于DES，该算法具有良好的安全性能；相对于RSA，该算法具有更高的效率。由此可见，这是一个具有良好的安全性能和较高的容错率的算法。

4 结 论

针对目前电子商务中存在的信息安全问题设计的这种混合[8]加密算法，它利用Logistic映射混沌状态的随机性使普通的穷举攻击破解变得遥不可及，又通过难以破译的离散对数问题保证了ECC对Logistic初始值的加密安全性。由此可见，该算法具有良好的安全性，但由于Logistic“一次一密”需要每次建立新的信道，这种局限性在一定程度上影响了算法的应用，我们将会在以后的研究工作中对算法做出相应的优化，以实现更高的效率并获得更好的效果。

参考文献：

[1] 冯登国.国内外信息安全研究现状及其发展趋势 [J].网络安全技术与应用，2001（1）：8-13.

[2] 唐礼勇，陈钟.电子商务技术及其安全问题 [J].计算机工程与应用，2000，36（7）：18-22.

[3] 韩凤英.一种基于改进Logistic混沌映射的图像加密算法 [J].中南林业科技大学学报，2008，28（1）：153-157.

[4] 张家树，肖先赐.基于广义混沌映射切换的混沌同步保密通信 [J].物理学报，2001，50（11）：2121-2125.

[5] 陈相琳，刘润涛，于存光.基于DES与ECC的混合数据加密算法 [J].哈尔滨理工大学学报，2007，12（1）：58-61.

[6] 龙强，刘小华.基于非对称密码体制的二维码加密算法 [J].重庆师范大学学报（自然科学版），2017，34（3）：91-95.

[7] 管春阳，高飞.一种基于混沌序列的加密算法 [J].北京理工大学学报，2003，23（3）：363-366.

[8] 闫茂德，纪志强，贺昱曜，等.AES与ECC混合加密算法的無线数据通信系统设计 [J]. 微电子学与计算机，2007，24（7）：135-138.