调压井托马临界稳定断面计算补充因素修正
2018-09-10洪振国田辉刘浩林
洪振国 田辉 刘浩林


摘要:对托马临界稳定断面计算补充电力系数、底部流速水头、水轮机效率变化等因素,采用加敦公式对托马临界稳定断面补充因素进行修正,并采用数学模型计算论证加敦公式计算临界稳定断面补充因素修正的合理性。结果表明:托马临界稳定断面计算补充电力系数、底部流速水头、水轮机效率变化等因素更为合理,机组转速、蜗壳压力和尾水管压力在安全可靠、经济合理范围内,加敦公式计算调压井的临界稳定断面是可行的。
关键词:调压井;托马临界稳定断面;加敦公式
中图分类号:TV332 文献标志码:A doi:10.3969/j.issn.1000-1379.2018.03.025
调压井利用自由水面有效反射由管道传来的水击波,改善压力管道的压力状态,改善机组在负荷变化时的供电质量及运行条件,以满足机组调节保证的技术要求。调压井临界稳定断面计算对调压井经济安全、水面波动衰减、水电站发电机组的稳定运行非常重要,目前随着许多水电站投入电网联合运行,电网容量加大,电网的系统和机电设备不断完善,整个电网分担负荷变化及调速器的稳定性能提高,单个水电站不承担调频任务,托马临界稳定断面不满足现代需求更为突出。近几年不少专家、学者对托马临界稳定断面补充因素进行了修正,但是调压井托马临界稳定断面补充因素修正相对复杂,目前补充因素的研究成果主要是近似的、半经验的计算公式,因此有必要对调压井托马临界稳定断面补充因素进行修正研究。
笔者通过托马临界稳定断面计算分析,对托马临界稳定断面补充了电力系数、底部流速水头、水轮机的效率变化、大波动的稳定条件因素,并采用加敦(Gandel )公式对托马临界稳定断面补充因素进行修正,采用数学模型计算论证加敦公式计算临界稳定断面的合理性。
1 工程概况
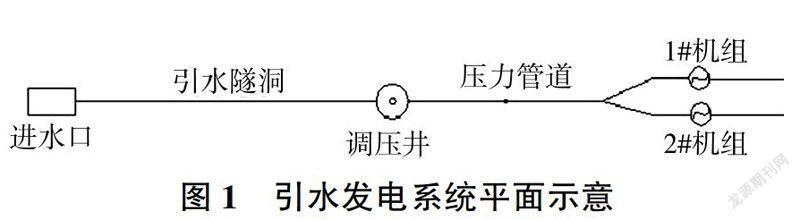
庙林电站位于云南省昭通市大关县和彝良县区域内金沙江一级支流洛泽河下游河段。庙林电站为径流式电站,开发河段为高山峡谷区,耕地稀少,其开发任务为单一水电开发,总装机容量65MW。水电站引水发电系统由进水口、引水隧洞、调压井、压力管道组成,引水发电系统平面示意见图1。
电站进水口布置在右岸坝体上,进水口孔口尺寸为6.5m×6.5m,底板高程为792.00m,顶高程819.00m。进水口经渐变段与引水隧洞相接。有压引水隧洞全长8157.506m,设计流量111.3m3/s,为直径6.5~7.3m的圆形断面,平均底坡坡比为0.3228%。洞身段根据地质条件,分别采用钢筋混凝土衬砌和喷混凝土衬砌,经统计,钢筋混凝土衬砌段占32%,喷混凝土段占68%。各种衬砌之间用渐变段相互连接。调压井位于转咀村下游380m的陡崖山体中,整个山体完整稳定、基岩出露。调压井采用阻抗式,主要由井筒、阻抗孔和交通洞组成,为地下式布置。调压井上游接引水隧洞,底板高程765.70m,井顶高程833.70m,井筒高68.00m,调压井阻抗孔内径为3.3m,井筒直径为17m,井壁衬砌厚1.0~1.2m。交通洞为城门洞形,尺寸4.5m×5.6m,长77m。调压井最低涌浪水位为785.21m,比洞顶高出1m3,最高涌浪水位为832.26m。压力管道上接调压井,下连电站厂房主阀。根据地形地质及工程总体枢纽布置要求等综合条件,全线采用地下埋管的布置形式。压力管道为一管双机的供水方式,上游进水口中心高程为768.40m,下端平管段中心线与机组安装高程同高,为718.19m。管道由主管、月牙岔管、支管及附件构成。主管管路包括两段地下平管、一段地下斜管。管道主管长194.5m,管径为5.4m;1#支管长26.1m,管径为3.4m;2#支管长25.5m,管径为3.4m。
2 托马临界稳定断面计算
水电站调压井临界稳定断面采用托马公式计算时,有以下假设:①调速器的灵敏度极高,达到理想的程度,使水轮机等出力调节;②水电站单独运行,使水电站成为孤立的电源;③忽略水輪机效率变化的影响;④水位波动振幅很小:⑤忽略引水管道管壁和水体的弹性;⑥忽略调压井底部的流速水头。托马公式为式中:Fth为托马临界稳定断面面积,m2;f为有压引水隧洞断面面积,m2;L为有压引水隧洞长度,m;H0为发电最小静水头,m;hwm为压力管道水头损失,m;hw0为有压隧洞水头损失,m;α为从水库至调压井的水头损失系数,α=hw0/V2,v为有压隧洞流速,m/s。
L=8 157.506m,f=38.36m2,H0=85.08m,hw0=10.261m,v=2.901m/s,α=1.219,hwm=4m,计算得到托马临界稳定断面面积Fth=208.29 m2。
3 托马临界稳定断面补充因素修正
3.1 补充电力系数因素
考虑庙林水电站并入云南省电网.参与“西电东送”和“云电外送”.整个电网分担负荷变化和调速器的性能提高,单个水电站不承担调频任务时,托马临界稳定断面补充电力系数因素修正为
式中:N为电站装机容量,kW;∑Ni为电力系统装机总容量,kW;β为无量纲参数。
按云南省电网2009年年底统计.云南省电网的系统总装机容量为3195万kW,庙林水电站总装机容量为6.5万kW,β=0.002,(3β-1)/2=-0.497,则补充电力系数因素修正后稳定断面面积<0.说明调压井的稳定断面不论如何小都不会出现失稳情况.它的稳定性可由电网系统中的其他机组来保证.由于电网规模较大.电站在电网系统中不承担调频任务.因此解除了调压井临界稳定断面控制。托马临界稳定断面补充电力系数因素修正后的临界稳定断面面积小于修正前的断面面积.所以整个电网分担负荷变化和调速器的性能提高等对调压井临界稳定性是有利的.提高了调压井水位的稳定性.降低了电站的出力变化幅度.托马临界稳定断面补充电力系数因素对波动的衰减是有利的。
3.2 补充底部流速水头因素
通过阻抗孔等连接引水隧洞和调压井时,在调压井底部存在流速水头.这个流速水头对引水隧洞而言是水头损失,托马临界稳定断面面积补充调压井底部流速水头因素修正为式中:V为调压井底部流速,m/s。
庙林水电站调压井底部流速V=2.092 m/s,则考虑底部流速水头相应的修正临界稳定断面面积为146.36m2。
托马临界稳定断面面积补充调压井底部流速水头后计算值小于修正前临界稳定断面面积(208.29m2),因此调压井底部流速水头在水电站运行过程中对波动的衰减是有利的。
3.3 补充水轮机的效率变化因素
实际上水轮机的效率是随流量和水头的变化而变化的.托马临界稳定断面面积补充水轮机效率变化因素修正为式中:H为水轮机的有效水头,m;η0为水电站正常运行情况下水轮机的效率:△H为负荷变化过程中发生的水头偏离量,m;△η为负荷变化过程中水轮机效率发生的相应的偏离量;△为无量纲参数。
η0=91.18%,△H=15.542m,△η=3%,△=0.18,因此计算得到托马临界稳定断面面积补充水轮机效率变化因素修正后为204.12m2。
补充水轮机效率变化因素后临界稳定断面面积修正值小于208.29m2,所以托马临界稳定断面补充水轮机效率变化因素同样对波动的衰减是有利的。
3.4 补充大波动的稳定条件因素
在大波动的情况下,水位波动过程线为正弦曲线,对于突然增加全部负荷的大波动情况.托马临界稳定断面补充大波动的稳定条件因素修正为式中:Z*为不考虑引水道水头损失时调压井水位波动的振幅,m。
计算得到补充大波动的稳定条件因素修正后的临界稳定断面面积为200.99m2,小于修正前的临界稳定断面面积(208.29m2),因此大波动的稳定条件同样对波动的衰减是有利的。
3.5 补充因素分析
根据上述计算可知:①由于修正前托马临界稳定断面面积计算假设水电站孤立运行、机组等出力调节和效率不变、水位波动振幅很小、忽略了调压井底部的流速水头、忽略引水管道管壁和水体的弹性等,因此计算的临界稳定断面面积偏大。②水电站并人云南省电网后,其稳定性可由电网系统中的其他机组来保证,所以托马临界稳定断面补充电力系数因素修正后的值<0,在5种计算方法中结果最小,今后电网规模日益扩大.托马临界稳定断面补充电力系数因素修正后可以基本解除调压井稳定断面的制约。③托马临界稳定断面面积补充电力系数、调压井底部流速水头、水轮机的效率变化、大波动的稳定条件因素后的计算值小于修正前的.所以这些补充因素对调压井的水面波动衰减是有利的,有必要对托马临界稳定断面补充因素深入研究。
4 综合因素补充修正
上述因素不是单一存在的.因此需要解决综合因素作用下托马临界稳定断面面积的修正问题。采用加敦公式在调压室微小振动稳定的托马条件基础上,补充综合因素对临界稳定断面面积进行修正。
4.1 综合因素补充修正计算
加敦公式为式中:λ为与调压室及引水道布置形状有关的系数,λ=0.7~1.0;h,为调压室底部引水道中的流速水头,m;Δ0为在t=LV/ghw0时间内可能产生规定的压力波衰减比;ε为并行运行率,ε=1-P0/Ps(P0为所设计发电站的负荷量,Ps为并列运行电网的总负荷);ρ、φ、ψ为与水轮机效率等特性有关的特征值。
按加敦公式计算补充综合因素修正后的临界稳定断面面积为-62.03m2<0,电站在系统中不承担调频任务,电站的稳定运行由系统来保证,与调压室面积的大小无关,解除了调压井稳定断面控制。
4.2 加敦公式计算合理性分析
根据庙林水电站引水隧洞、调压井、压力管道、岔管、支管、调速器和水轮发电机组布置,建立水电站引水发电系统整体数学模型,将水轮机模型综合特性曲线以离散数据点的形式在计算机中储存,对引水发电系统各压力管段进行分段处理。按加敦公式计算调压井临界稳定断面,采用文献数学模型计算,论证加敦公式计算调压井稳定断面的合理性。
数学模型计算结果表明:在最大水头下2台机组同时甩满负荷时,水轮机导叶关闭按一段直线关闭规律,关闭时间控制在7s,蜗壳最大压力上升率为18.2%,压力水头升高值为98.53m<79.2m,蜗壳最大水锤压力升高值控制在调压室最大涌波水位附近,蜗壳压力在经济合理范围内,具有良好的机组调节品质。机组转速上升值为376.53r/min,上升率35.15%,小于规范要求(60%),转速上升值在经济合理的范围内,水电站运行安全可靠、经济合理。尾水管最低压力水头为-1.86m,真空度大于-8m,机组额定负荷波动4%,调速器振荡次数小于1次,调节时间小于25s,超调量小,转速最大偏差仅3%左右,水电站负荷波动稳定,发电机组安全运行。在水轮机全部运行范围内,水轮机径向轴承的垂直振动位移不超过60μm,且不发生共振,进水阀在兩侧压力差不大于30%的最大静水压范围内能正常开启,且不产生强烈振动,尾水管内压力水头脉动值不大于额定水头的11%,水轮机最高效率保证值不低于94.85%,因此水轮机无有害的振力和压力脉动,长期运行是稳定的。
由上述分析可知:尾水管最低压力满足《水力发电厂机电设计规范》[6]要求,机组转速、蜗壳压力和尾水管压力在安全可靠、经济合理范围内,水轮机无有害的振力和压力脉动,长期运行是稳定的,因此加敦公式计算调压井的稳定断面面积是可行的,解决了托马临界稳定断面补充综合因素修正技术难题。
5 结论
(1)由于托马临界稳定断面计算假设水电站孤立运行、机组等出力调节和效率不变、水位波动振幅很小、忽略调压井底部的流速水头、忽略引水管道管壁和水体的弹性等,因此计算的托马临界稳定断面面积偏大。
(2)托马临界稳定断面补充电力系数、调压井底部流速水头、水轮机的效率变化、大波动的稳定条件因素后的计算值小于修正前的。
(3)尾水管最低压力满足《水力发电厂机电设计规范》要求,机组转速、蜗壳压力和尾水管压力在安全可靠、经济合理范围内,水轮机无有害的振力和压力脉动,长期运行是稳定的,因此加墩公式计算调压井的稳定断面积是可行的,同时解决了托马临界稳定断面补充综合因素修正技术难题。今后仍要进一步开展调压井稳定断面计算方法研究和模型试验工作,有效了解调压井水面波动的衰减情况,设计出新型经济的调压井,以确保水电站负荷波动稳定和发电机组安全运行。
参考文献:
[1]中华人民共和国水利部.水利水电工程调压室设计规范:SL655-2014[S].北京:中国水利水电出版社,2014:1-15.
[2]潘家铮,傅华.水工隧洞和调压室:调压室部分[M].北京:水利电力出版社,1992;52-73.
[3]水利水电规划设计总院.水工设计手册:水电站建筑物[M].北京:中国水利水电出版社,2013;98-120.
[4]洪振国,刘浩林.阻抗式调压井水力学计算研究[J].水力发电,2014,40(12):51-54.
[5]洪振国,刘浩林.水电站调压井特征线法水力计算研究[J].中国农村水利水电,2015(4):163-166.
[6]中华人民共和国国家发展和改革委员会.水力发电厂机电设计规范:DL/T 5186-2004[S].北京:中国电力出版社,2004:1-10.
