基于偏相关法的暴雨管理模型参数敏感性分析

段明印 李传奇 肖学 韩典乘

摘要：基于拉丁超立方抽样法对暴雨管理模型（SWMM）输入参数进行采样，采用偏相关法对参数进行全局敏感性分析。取某小区为研究区域构建SWMM模型，分析水文水力参数变化对模型输出变量的影响大小。研究发现，峰值流量最敏感的参数是透水区糙率系数，但该系数并不起决定性作用，它和其他较敏感参数共同决定着峰值流量的大小；峰现时间最敏感的参数是最小渗透率，但是所有参数的敏感性都较低，对峰现时间的影响都很小；总产流量最敏感的参数依次是最小渗透率、面积修正因子、渗透衰减系数和最大渗透率。通过敏感性分析识别出敏感参数，可提高参数率定效率和模拟结果的可靠性。

关键词：SWMM模型；逐步回归；偏相关；全局敏感性

中图分类号：X143 文献标志码：A doi：10.3969/j.issn.1000-1379.2018.03.003

1 研究背景

城市化在促进我国经济发展的同时也改变了城市下垫面的属性，使得城市雨洪灾害等问题日益突出，严重威胁着人民生命财产安全[1]。暴雨管理模型（SWMM）可以动态模拟降雨径流过程及雨水在管网中的传输过程，能够用来管理城市雨洪以及指导海绵城市的建设，因此在国内很多地区得到了广泛运用[2]。

参数率定是精确构建SWMM模型的前提，但是SWMM模型参数较多，参数率定效率非常低，因此需要对SWMM模型进行参数敏感性分析，降低参数的不确定性，识别出重要参数进行重点率定，不重要参数可取经验值[3]。参数敏感性分析的方法可以分成两大类：一类是局部敏感性分析方法，大多使用Morris法；另一类是全局敏感性分析方法，主要有多元回归法、FAST法、RSA法、Sobol法、偏相關法等[4]。局部敏感性分析方法只能反映单个自变量对模型结果的影响，忽略了自变量之间的相互作用对模型结果的影响，无法在“异参等效”的情况下得到精确解；全局敏感性分析方法能够反映所有自变量以及自变量之间的相互作用对模型结果的影响，适用于参数众多且存在“异参等效”的模型[5]。因此，全局敏感性分析方法逐渐成为研究热点，张质明等[6]通过Sobol法对WASP模型中的参数进行了敏感性分析，有效识别出了敏感参数；王浩昌等[7]通过逐步回归法有效识别出了对SWMM模型径流影响最大的参数；Yi X.等[8]通过Morrisscreening法找出了三维水质模型的敏感参数MarinoS.等[9]通过偏相关法精确地得出了各个参数的敏感性。

与其他全局敏感性分析方法相比，偏相关法能够在控制其他参数影响的条件下得到较为精确的参数敏感性。本文以长沙市雅华花园小区为例，采用偏相关法对SWMM模型输入参数和输出结果间的复杂关系进行敏感性分析，并与逐步回归法得到的结果进行对比，以期为下一步的参数率定提供参考，为精确、高效建模打下基础。

2 资料和方法

2.1 SWMM模型构建

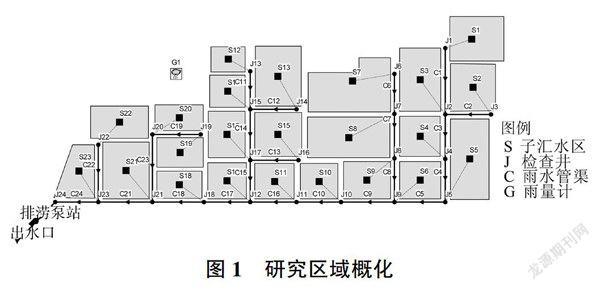
选取长沙市雅华花园小区作为研究区域[10]，该区域总面积11.71hm2，不透水区域主要为屋面和道路，占地面积为6.56hm2，透水区域占地面积为5.15hm2。根据该小区的地形资料、房屋分布资料以及管网分布资料，将研究区域划分为23个子汇水区，包括24个检查井节点、24条雨水管渠、1个排涝泵站和1个出水口，下渗模型采用Horton模型，研究区域概化见图1。

2.2 参数取值

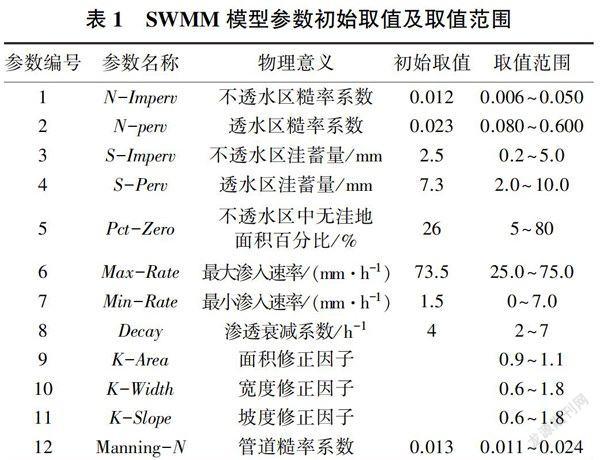
SWMM模型中与降雨径流模拟相关的参数共计14个，其中子汇水区不透水区域面积和管渠长度在测量时误差较小，可直接使用量测值，因此只需对剩余的参数进行敏感性分析。剩余12个参数中子汇水区面积、坡度和特征宽度这3个参数具有明显的空间特性，在测量过程中存在误差以及在概化模型时存在主观性，因此引入3个修正因子：面积修正因子（K-Area）、宽度修正因子（K- With）和坡度修正因子（K-Slope），相应的输入参数为测量值和对应修正因子的乘积[7]。12个参数的初始取值均为实测值，参数的取值范围根据SWMM建模手册和相关研究确定，并结合国内实际情况对某些参数的范围进行调整。参数初始取值和取值范围见表1。

2.3 逐步回归法

逐步回归法是以多元线性回归分析方法为理论基础的一种回归分析方法，旨在建立最优的回归方程，使得回归方程中只含有对输出结果影响较大的输入变量，不含有对输出结果影响微弱的输入变量。该方法在分析过程中首先计算所有选人回归方程的输入变量的偏回归平方和，挑选出偏回归平方和最小的输入变量，通过方差比在给定F（置信度）水平下进行显著性检验。若结果显著，则回归方程保留该输入变量以及剩余所有输入变量；若结果不显著，则剔除该输入变量，然后对剩余输入变量按照偏回归平方和由小到大的顺序依次进行显著性检验，直到检验结果为显著时结束。接着，在未引进回归方程的全部输入变量中挑选出偏回归平方和最大的输入变量，通过方差比在给定F水平下进行显著性检验，若结果显著，则该输入参数选人回归方程，然后按照偏回归平方和由大到小的顺序依次对剩余输入变量进行检验，直到检验结果为不显著为止。输入参数的选人过程和剔除过程不断循环，直到回归方程外无符合选人条件的输入参数，回归方程内无符合剔除条件的输入参数为止[7]。

可用逐步回归法对参数进行全局敏感性分析，具体含义：未选人回归方程的参数即为不敏感参数，被选人回归方程的参数即为敏感参数；决定系数（R2）的值表示模型输出结果确定性所占的比例；标准回归系数（SRC）的绝对值代表了参数敏感性大小，SRC的符号代表了参数与输出结果是正相关还是负相关。

2.4 偏相关法

运用多元相关分析方法进行参数敏感性分析时，简单的相关系数并不能如实反映出参数和输出结果的相关性，原因是参数众多且关系复杂，某一参数和输出结果的相关性可能会受到其他参数的影响。若想客观反映某一参数和输出结果的相关关系，则要消除其他参数的影响。偏相关分析就是一种控制其他变量影

2.5 拉丁超立方抽样

分析参数的敏感性需要在参数的分布范围内进行抽样，常用的抽样方法有蒙特卡洛抽样法和拉丁超立方抽样法。前者属于简单随机抽样，容易出现样本点集中的现象，导致抽样效率低下；后者属于分层随机抽样，能够在参数分布范围内均匀采集样本点。本文采用拉丁超立方抽样法[12]。

运用拉丁超立方抽样法在12个参数的分布范围内进行分层抽样，随机生成1 000组参数。利用Matlab将生成的1000组参数依次替换SWMM输入文件中的12个参数，得到1000组SWMM输入文件。依次运行模拟得到的1000组SWMM输入文件，生成1000组SWMM输出文件。选择峰值流量、峰现时间以及总产流量3个具有重要意义的模拟结果作为输出，利用Matlab编程提取1000组SWMM输出文件中出水口处3个输出变量的信息，分别采用逐步回归法和偏相关法进行参数的全局敏感性分析。

2.6 降雨数据

降雨资料采用研究区域实测降雨数据，选取场次编号为2004721的实测降雨，该场降雨共历时10h，降雨量为117mm，降雨强度过程见图2。

3 结果和分析

3.1 初步分析

为初步了解SWMM模型12个输入参数和3个输出变量的相关关系，利用1000组SWMM输入参数和输出结果画出残差散点图，对输入参数和控制参数进行多元线性回归分析，求得输入参数和控制参数的残差作为残差散点图的横坐标，对输出结果和控制参数进行多元线性回归分析，求得输出结果和控制参数的残差作为残差散点图的纵坐标。通过残差散点图可以看出，SWMM模型的输入参数和输出结果之间大多具有较强的线性关系，N-perv、Max-Rate、Min-Rate、Decay、K-Width和峰值流量之间具有较强的线性关系，其中N perv、Max-Rate、Min-Rate与峰值流量成负相关，Decay和K-Width与峰值流量成正相关；N-Imperv、Manning-N与峰现时间成正相关；Min-Rate与总产流量呈现出很高的负相关性。

3.2 逐步回归分析

采用逐步回归法分析SWMM模型中输出结果对参数的敏感性，结果见表2。由表2可知：峰值流量最敏感的参数为N-perv，但其SRC绝对值为0.454，敏感性较低，且引入该参数的决定系数R2仅为0.193，这说明N-perv虽然是最敏感参数，但是对峰值流量并不起决定性作用，回归模型的R2最终为0.918，说明输入参数和峰值流量之间有着较强的线性关系；对峰现时间来说，各个参数的SRC值比较平衡且绝对值都偏小，说明各个参数的敏感性都比较低，对峰现时间影响较小，并且最终的R2仅为0.183，说明输入参数和峰现时间的线性关系较差；总产流量最敏感的参数是Min-Rate，该参数的SRC绝对值为0.849，是敏感参数；K-Area的敏感性仅次于Min-Rate，引入Min -Rate和K-Area后的R2值达到了0.897，说明Min-Rate和K-Area对总产流量起着决定性作用，最终的R2为0.975，说明输入参数和总产流之间有着显著的线性关系。

3.3 偏相关分析

利用Matlab对输入参数和输出结果进行偏相关分析，结果见表3。由表3可知：对峰值流量来说，N-perv为最敏感参数，r值（偏相关系数）为-0.845，Decay、Min-Rate、K-Width、Max-Rate、K-Area这5个参数；值的绝对值都在0.7以上，说明N-perv虽然是最敏感参数，但是并不起决定性作用，它和后面的5个参数共同影响峰值流量的大小，其中N-perv、Min-Rate、Max-Rate与峰值流量成线性负相关，这3个参数的增大将会使地表曼宁系数增大、径流流速降低、雨水下渗量和下渗时间增大，从而使得峰值流量减小；Decay、K-Width、K-Area與峰值流量成线性正相关，这3个参数的增大将会使汇水面积增大、径流总量增大、下渗量减小，从而使得峰值流量增大。对峰现时间来说，所有参数r值都偏小，说明各个参数对峰现时间的影响都比较小，其中Min-Rate为最敏感参数，r值为0.253。对总产流量来说，Min-Rate、K-Area、Decay、Max-Rate均为高敏感参数，r值的绝对值都在0.7以上，这4个参数对总产流量起主要影响，其中Min-Rate为最敏感参数，r值的绝对值高达0.983；Min-Rate、Max-Rate与总产流量成线性负相关，这2个参数的增大将会使下渗量增大，从而使总径流量减少；K-Area、Decay与总产流量成线性正相关，这两个参数的增大将会使汇水面积增大、雨水下渗量减小，从而使总产流量增大。

将偏相关法的分析结果与逐步回归法的进行对比，发现偏相关法对输入参数和输出结果的线性关系以及参数敏感性由大到小的排序和逐步回归法得出的结果一致，这说明偏相关法能够有效识别出输入参数和输出结果的线性关系以及参数的敏感性顺序。

对于峰值流量，逐步回归法识别出的较敏感参数有6个，偏相关法识别出的较敏感参数有8个；对于峰现时间，两种方法识别出的相对较敏感参数都只有2个；对于总产流量，逐步回归法识别出的较敏感参数有2个，偏相关法识别出的较敏感参数有4个；对于同一参数的敏感性，偏相关法得到的值大于逐步回归法的。出现这些现象的原因是逐步回归法以多元线性回归法为理论基础建立最优的回归模型，其在分析自变量和因变量的相关关系时只是求得简单的相关系数，并未考虑其他自变量对相关系数的影响，因此求得的相关系数并不具有客观性，往往无法识别个别敏感参数，而偏相关法能够在消除其他变量影响的条件下求得两个变量的相关系数，因此偏相关法比逐步回归法求得的参数敏感性更加精确，且能够有效识别出所有敏感参数。Min-Rate、Max -Rate、Decay这3个参数是Horton下渗模型相关参数，敏感性均在前5位，可见Horton下渗模型相关参数对3个输出变量均有重要影响。

4 结语

（1）偏相关法和逐步回归法都能对SWMM模型的参数进行全局敏感性分析，也都能有效识别出输入参数和输出结果的线性关系以及参数的敏感性顺序，但是逐步回归法不能准确识别参数的敏感性，而偏相关法能够更加精确地识别参数的敏感性，且能识别出所有敏感参数，更适用于复杂水文模型的参数敏感性分析。

（2）由偏相关法和逐步回归法的分析结果可知，峰值流量最敏感的参数是N-perv，它和Decay、Min-Rate、K-Width、Max-Rate、K-Area共同影响峰值流量的大小；对峰现时间来说，各个参数的敏感性都很低，其中Min-Rate是最敏感参数；总产流量最敏感的参数是Min-Rate，它和K-Area、Decay、Max-Rate一起对总产流量起着决定性作用；Horton下渗模型的相关参数Min-Rate、Max-Rate、Decay均为较敏感参数。

（3）经过参数敏感性分析，可降低参数的不确定性，提高模型参数率定效率，为精确、高效建模打下基础。

参考文献：

[1]YU H，HUANG G，WU C.Application of the StormwaterManagement Model to a Piedmont City：a Case Study ofJinan City，China[J].Water Science and Technology，2014，70（5）：858-864.

[2]陈晓燕，张娜，吴芳芳，等.雨洪管理模型SWMM的原理、参数和应用[J].中国给水排水，2013，29（4）；4-7.

[3]林杰，黄金良，杜鹏飞，等.城市降雨径流水文模拟的参数局部灵敏度及其稳定性分析[J].环境科学，2010，31（9）：2023-2028.

[4]谭明豪，姚娟娟，张智，等.基于Morris的SWMM水质参数灵敏度分析与应用[J].水资源与水工程学报，2015，26（6）：117-122.

[5]宋晓猛，张建云，占车生，等.水文模型参数敏感性分析方法评述[J].水利水电科技进展，2015，35（6）：105-112.

[6]张质明，王晓燕，李明涛.基于全局敏感性分析方法的WASP模型不确定性分析[J].中国环境科学，2014，34（5）：1336-1346.

[7]王浩昌，杜鹏飞，赵冬泉，等.城市降雨径流模型參数全局灵敏度分析[J].中国环境科学，2008，28（8）；725-729.

[8]YI X，ZOU R，GUOHC.Global Sensitivity Analysis of aThree-Dimensional Nutrients-Algae Dynamic Model for aLarge Shallow Lake[J].Ecological Modelling，2016，327：74-84.

[9]MARINO S，HOGUE I B，RAY C J.A Methodology for Per-forming Global Uncertainty and Sensitivity Analysis inSystems Biology[J].Journal of Theoretical Biology，2008，254（1）：178-196.

[10]任伯帜.城市设计暴雨及雨水径流计算模型研究[D].重庆：重庆大学，2004：120-131.

[11]熊剑智.城市雨洪模型参数敏感性分析与率定[D].济南：山东大学，2016：18-19.

[12]郑震，张静，宫辉力.MIKE-SHE水文模型参数的不确定性研究[J].人民黄河，2015，37（1）：23-26.