地下水数值模拟与可视化建模系统框架研究

闫静 李立国

摘要：针对现有孔隙地下水有限元数值模拟在三维可视化与空间分析等方面存在的不足，以有限元数值计算方法和3D GIS平台为基础，结合GIS空间分析算法和计算机图形学理论，提出了孔隙地下水有限元分析过程的概念模型的构建、含水层介质的空间离散、水文地质参数提取与赋值等关健步骤，给出了孔隙地下水有限元数值模拟过程在3D GIS下的实现方法和技术框架。该技术框架旨在简化有限元分析流程、优化模型计算效率、实现地下水有限元数值模拟过程及计算结果的三维可视化。结果表明：基于3DGIS构建的三维水文地质模型，可充分反映地下水系统在3D空间上的分布特征，形成合理的水文地质概念模型，所提出的自适应格网动态生成机制，能够有效改进有限元数值模拟精度和效率。

关键词：有限元数值模拟；3D GIS；水文地质建模；模型计算参数；可视化

中图分类号：TV211.1+2 文献标志码：A doi：10.3969/j.issn.1000-1379.2018.03.018

地下水有限元数值模拟是对地下水进行定量评估与预测的重要手段，目前国际上已有很多成熟的地下水数值模拟软件，如MODFLOW、FEFLOW、GMS等，这些软件功能齐全，能够有效支持地下水的数值模拟。近年来，随着GIS理论逐渐成熟与普及，一些学者开始研究利用GIS技术实现地下水数值模拟，Venkatesh Uddameri等建立了多重标准地下水流最优路径模拟的GIS辅助决策体系；Elkadi A I等基于GIS建立了面向区域特征的地下水流模拟模型；孙继成等综合运用FEFLOW软件和GIS技术，对甘肃省秦王川盆地的水文地质条件进行概化，建立了该地区的地下水数值模拟模型；陈锁忠等研究了基于GIS的不规则六面体含水层三维空间离散方法，给出了GIS下孔隙地下水流非稳定运动过程数值模型参数的自动提取方法，有效提高了模拟精度。随着3D GIS技术的发展，数值计算过程及模拟结果的可视化逐渐成为研究热点，武强等研究了地下水渗流场的动态模拟可视化方法，毕振波等开发了地下水有限元计算可视化系统。

将GIS技术引入数值模拟过程，有利于兼顾数值模型参数的空间特性与精度，提高模型空间分析能力和数据管理效率，使地下水数值模拟更具空间辅助决策特性。笔者基于地下水有限元数值模拟的基本原理，研究了3D GIS下孔隙承压非稳定地下水有限元数值模拟实现及可视化方法。基于改进前沿推进法（AFT）生成三角形空间离散格网，该方法具有边界拟合度高、单元尺寸可随水力梯度自适应的特点；根据三维地质建模理论和空间分析算法，构建三维水文地质模型及其空间分析方法；采用格网约束局部拓扑重建算法提高参数提取精度，基于局部分块插值技术和计算机图形学理论实现模型参数的自动赋值；通过三维水流场、三维水文地质模型及其集成形式对计算结果进行可视化。

1 研究区地下水概念模型构建

1.1 研究区水文地质条件

研究区属于盐城滨海平原水文地质分区，位于黄海之滨，介于32°75′-34°42′N，119°34′-120°41′E。该平原由2000～3000a来海水和河流不断冲积而成，区域内水网密布，形成滨海水网平原地貌类型，至今仍在不断向海延伸。研究区地势低平，从东南向西北缓慢倾斜。大丰境内地势较高，海拔3.00～5.00m，向北逐渐降低，到射阳河处为1.00～1.50m。研究区承压地下水主要赋存于松散沉积岩层孔隙中，埋深为50.00～350.00m。

研究区内含水层多为由粉砂、细砂、粗砂、砾石等组成的松散沉积岩类含水层，含水量充沛，水量稳定，不同含水层之间由黏土或淤泥质黏土层形成隔水层。根据沉积物时代、成因、地层结构以及水文地质特征分析，区内包含孔隙潜水含水层、第Ⅰ承压含水层、第Ⅱ承压含水层、第Ⅲ承压含水层、第Ⅳ承压含水层5个含水层组（见图1），其中：孔隙潜水或微承壓水主要接受大气降水、地表水、农业灌溉水入渗补给，排泄为蒸发和开采利用；第Ⅰ承压水、第Ⅱ承压水为微咸水、半咸水、咸水；第Ⅲ承压含水层由下更新统中细砂、中粗砂组成，厚度为20.00～35.00m，富水性较好，为研究区地下水的主开采层；下伏新近系地层中发育有第Ⅳ、第Ⅴ承压含水层组，接受上部越流补给和西中部山体的侧向补给，主要排泄方式为人工开采。

1.2 地下水连续性运动方程

通常可采用如下连续性运动方程描述地下水的非稳定运动：式中：Kz为越流补给系数；dz为越流经过的垂直距离；Th为含水层水平方向的导水系数；W为单位时间、单位面积上含水层垂向补给水量（流出以负值表示）；S为含水层贮水系数；Hz为水头；H为待计算水头；D为渗流区，为一类边界Г1和二类边界Г2包围的研究区域；H（x，y，0）为初始时刻水头的二维空间分布函数；H0（x，y）为任意位置处初始水头；q为边界上单位宽度内流入的流量（流出取负值）；n为外法线方向；t为模拟时段；φ（x，y，t）为指定时间t位置（x，y）处的地下水水位；T为导水系数。

1.3 系统技术框架概述

由上述地下水连续性运动方程数值计算过程可知，3D GIS技术与地下水数值模拟进行结合的切入点主要体现在如下几个方面。

（1）水文地质概念模型建立。孔隙地下水系统空间分布连续，不同含水层之间的水力联系受含水层空间结构特征影响明显，为反映地下水系统在三维空间的分布特征，引入三维地质建模理论辅助构建水文地质概念模型。

（2）空间离散格网生成。离散格网生成是进行地下水有限元数值模拟前处理的重要环节，格网单元的形态、尺寸对有限元模拟精度和计算效率有较大影响，为兼顾计算精度和效率，一般要求三角单元尺寸与不同水力梯度相适应，且相邻单元之间尺寸过渡尽量平缓，避免出现狭长三角形，同时需顾及含水层空间分布特征以及越流补给等约束条件。笔者采用改进前沿推进法生成模拟区域自适应三角形空间离散格网，综合考虑水力梯度、边界条件、含水层结构等约束条件，获取局部区域最优单元尺寸，动态生成新的自适应空间离散格网。

（3）模型参数提取与初始条件赋值。地下水数值模拟模型参数具有明显空间分布特性，依据其空间分布特征，抽象为点、线、面矢量数据，对计算单元和水文地质参数矢量数据进行叠置分析，实现计算参数的自动提取。根据模拟初始时刻目标含水层初始水头空间分布、边界条件、地下水的开采补给排泄、各水文地质参数空间分布情况，结合空间插值算法将模型计算参数自动赋值到计算单元或格网节点上。

（4）模拟结果可视化。采用2.5D水位DEM和3D地下水流场等可视化表达形式，将地下水流场与三维空间数据模型集成即可得到三维水文地质空间数据模型。

三维空间数据模型由一系列形态各异的体元组成，这些离散的体元一方面能够拟合水文地质对象的空间结构特征，另一方面是地下水非稳定运动有限元模型与空间数据模型实现耦合的桥梁。这种耦合机制包含如下两个方面：在有限元数值模拟过程中将计算格网的节点置于空间数据模型所使用体元的节点处，每个节点的参数值可依据相关算法从空间数据模型中自动提取，实现空间数据模型参数向有限元模型的传输；随着模拟时段的推进，数值模拟计算结果不断发生改变，将计算结果实时回馈到空间数据模型的体元节点上，并驱动其空间结构做出相应调整。通过以上机制，即可实现空间数据模型和地下水数值模型之间参数的双向传输及互相作用。

2 关键技术研究

2.1 基于广义三棱柱（GTP）的三维水文地质建模与空间分析

基于GTP的三维水文地质建模的关键步骤：①地质钻孔建模，整理水文地质钻孔数据，结合数据特征提取隔水层与含水层信息，构建控制性水文地质钻孔模型；②含水层界面建模，确定模拟区域边界范围，基于空间插值算法构建各含水层顶、底板三角网（TIN）模型；③GTP体元构建，将相邻含水层界面上的格网节点依据空间关系组织成GTP体元，使得单个GTP体元不与其他GTP体元交叉、重叠，且不会跨越不同类型含水层；④构建含水层模型，GTP体元包含属性信息，属性相同的GTP体元组成三维地质体模型。研究区地下水系统及第Ⅲ承压含水层三维模型见图2。

为辅助概念模型的空间认知，可进一步开发空间分析模块，即基于GTP的剖切算法对三维模型进行空间剖切、剖面图提取、空间开挖等，实现对地下水系统的多角度可视化表达；基于向量场可视化方法，绘制不同时刻的三维地下水流场模型，以反映地下水的时空动态变化特征。

2.2 基于改进前沿推进法（AFT）的自适应空间离散格网构建

AFT应用较为广泛，所得格网对复杂边界拟合度高、自适应性好，单元之间尺寸过渡平滑，能够满足有限元数值模拟要求。在AFT的格网生成算法中，根据背景格网动态获取单元尺寸，是实现格网自适应性的关键。将水位DEM作为背景格网，建立水力梯度和单元控制尺寸之间的映射关系，预估剖分最大单元尺寸hmax及最小单元尺寸hmin，计算区域内部最大水力梯度Vmax和最小水力梯度Vmin。水力梯度Vi和对应单元尺寸hi之间的关系可用下式近似表示：

水力梯度的计算方法可参阅文献，在此不再赘述。将式（4）对应关系代入AFT算法，即可得到格网单元尺寸随水力梯度自适应的空间离散格网。对于地下水数值模拟问题，考虑到区域离散受区域内点、线以及面状地理要素的约束，且前沿边推进过程中不可避免地出现“交汇”效应，导致所得离散格网在局部区域可能出现单元尺寸过渡不平滑、三角形形态差等问题，因此引入Laplace光顺算子对AFT离散格网进行优化。选取2014年10月第111承压含水层作为地下水水位 DEM背景格网构建自适应有限元离散格网，预设最大单元尺寸hmax为4km，最小单元尺寸hmin为2km，格网生成结果见图3。

2.3 基于格网拓扑重建的面状参数提取

由于水文地质含水层在空间上是连续的，大多地下水数值模拟计算参数在空间上呈面状分布，因此参照已建概念模型和抽水试验数据，将模拟含水层划分为若干个水文地质参数分区，使得每个分区内部含水層近似为均质。参数分区在空间上为不规则多边形，通过将分区多边形与离散格网进行叠置分析实现计算参数的自动提取，但存在一个单元同时分布于多个水文地质参数分区的情况，见图4，单元ABC同时跨越了参数分区P1、P2、P3，此时无法确定单元属于哪一个分区，给单元参数提取带来一定困扰。

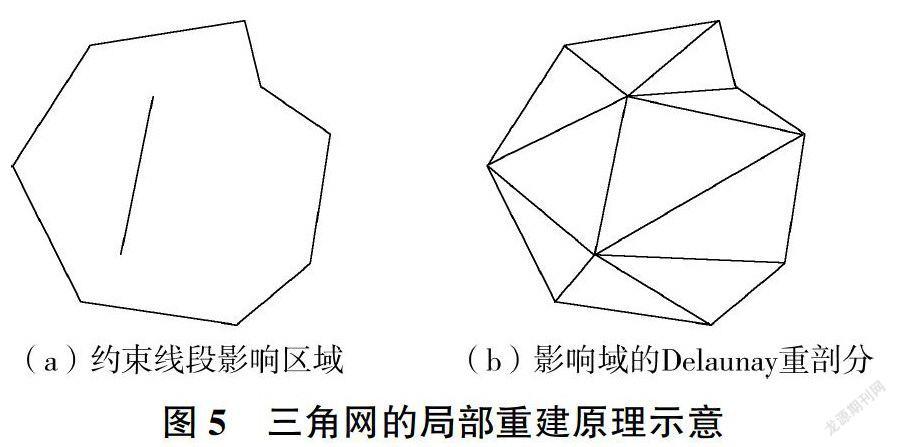
为保证单元内部水文地质参数的一元性，提出参数分区约束的三角网局部拓扑重建算法，将原空间离散格网转换为分区边界线约束的三角格网，使每个单元都完全位于单个参数分区内部。分区边界线约束格网拓扑重建过程：①对于位于分区边界线上的一个线段，搜索该线段起点和终点所在的三角形索引；②确定该线段影响到的三角形组成的影响域；③删除影响域内部的原有三角形，以该线段为起始边，调用Delaunay算法，重剖分影响域的三角网；④获取分区边界线上的下一条线段，重复步骤①一③，直至遍历所有线段，见图5。

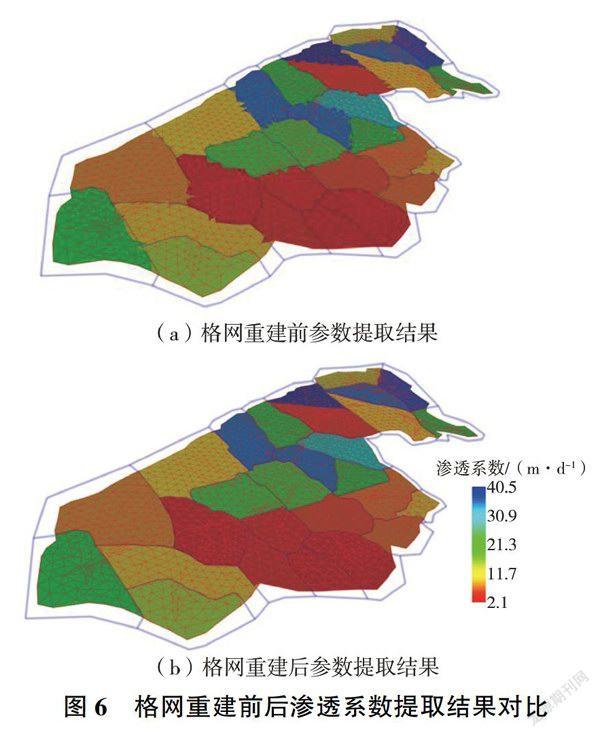
在拓扑重建得到的约束格网中，每个三角单元仅分布于单一的参数分区内，格网单元内部水文地质条件及参数等有较好的代表性和一元性。此时，采用简单的射线法即可快速获取三角形叠合的参数分区，从而完成单元水文地质参数的自动提取。格网拓扑重建前后渗透系数提取结果对比见图6，可以看出，拓扑重建后格网的计算参数提取结果与参数分区在范围上更匹配。

2.4 点状分布的计算参数可视化赋值

对于线状分布的计算参数，如边界流量、河流水位、河床渗透系数等，可将其对应的线状要素通过线约束格网拓扑重建的方式归人离散格网，过程较简单，因此重点讨论点状分布参数的可视化赋值方法。

地下水数值模拟模型点状分布参数主要包括地下水开采量和地下水水位，地下水开采量由模拟区内的开采井决定，地下水水位数据来源于模拟区域内的动态监测井。在地下水流有限元数值计算中，开采量和地下水水位在空间上虽然均以点状分布，但二者之间的空间分布特征并不一致：地下水水位由含水层的空间分布决定，孔隙地下水含水层具有空间连续性，地下水水位数据在空间上呈连续分布；地下水开采则由人类活动引起，不同开采井之间相互作用有限，开采井在空间上可视作以离散点的形式存在。故对于以上两种点状参数，应采用不同的可视化赋值方法。

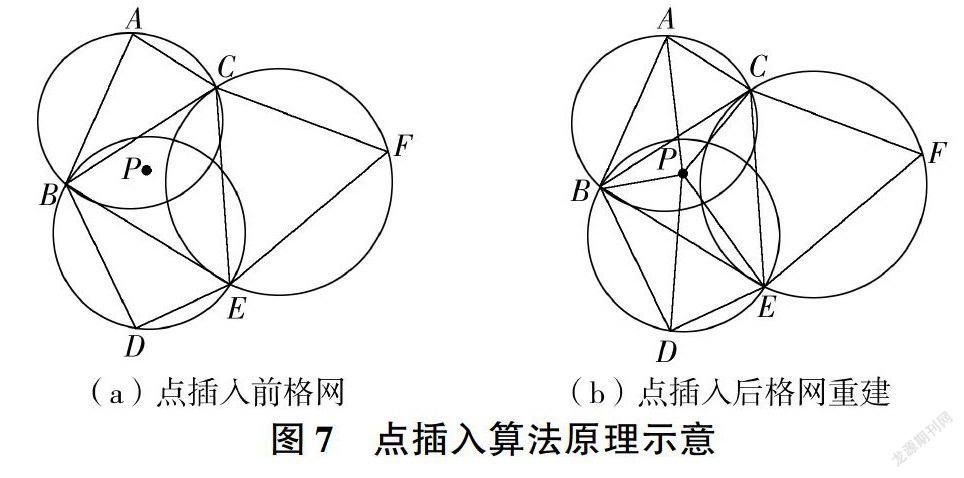
（1）初始水位賦值。水位监测井可提供水位的实际数据作为预报结果精度评价的依据，在进行离散格网生成之后，需把监测井作为新的格网节点插入离散格网中。如图7所示，点P表示监测井，获取包含尸点的单元BCE，搜寻与BCE相邻的三角形单元，判断P点是否位于相邻三角形的外接圆内。若点P位于相邻三角形外接圆内，则删除该邻边，分别连接P点和相邻三角形的三个顶点构建新的三角形；若点P不位于相邻三角形外接圆内，直接连接P与邻边的两个端点构建新三角形。之后根据设定的初始时刻，查询数据库中每个监测井在该时刻下的实测水位。调用空间插值算法，形成初始水位场，分配到离散格网节点上，完成初始水位赋值。

（2）开采量赋值。数值模拟中开采量指某单元单位面积上的地下水开采量，开采量的赋值方法：在离散格网中查询包含开采井的三角单元，计算该单元上单位面积、单位时间的地下水开采量，并将该值赋予该三角单元，其他不包含开采井的单元的开采量赋值为0。

在3D GIS环境下，盐城市第Ⅲ承压含水层2014年10月地下水水位及开采量可视化赋值效果见图8，图中柱体表示开采井模型，计算格网中红色区域表示地下水开采量为0，其他颜色则对应不同的开采量，其颜色特征为单调离散着色；水位赋值结果以水位DEM的形式可视化，其颜色特点为连续光滑过渡。

上述可视化过程基于3D GIS平台，实现了对水文地质参数数据的组织、管理、提取与赋值。不同的赋值模块以独立子程序包的形式分别设计开发，封装成独立插件集成到数值模拟平台，实现各模块之间的松耦合和模块化，为数值模拟的试算、拟合等提供科学计算可视化工具。

2.5 水文地质参数及其分布特征

为实现地下水流动态变化特征的表达，分析数值模拟以及系统动态建模时有限元数值计算的参数，见表1。

2.6 地下水流速的三维可视化

地下水流模拟输出结果为离散格网上每个计算节点的水位，一般采用三维流场的形式对地下水流模拟结果进行可视化。根据地下水渗流特点，三维流场的数据源是地下水渗流速度，其方向代表地下水流动方向。对于二维地下水流有限元数值模拟，每个格网节点上的流速可通过X、Y方向上的速度分量：vi、vj合成得到。根据达西定律，计算节点上某方向的渗流速度与节点位置处水力梯度成正比。式中：v为渗流速度；H为水位场；l为某个渗流方向；kl为沿l方向的渗透系数。

求渗流速度的关键是获取表示水位空间分布的函数H的表达式。对于某个节点i，将其周围一定范围的水位曲面视作一个二次曲面，该曲面表达式为

Hi（x，y）=b0+b1x+b2y+b3x2+b4xy+b5y2（6）式中：x、y、z为空间位置坐标在三个坐标轴上的投影；b0、b1、…、b5为系数。

该范围内至少有6个离散格网点，列出这6个计算节点的误差方程矩阵：式中：x1、x2、…、x6，y1、y2、…、y6为估测值；Z1、Z2、…、Z6为误差值。

根据平差理论，求得系数矩阵B的解为

B=（MTPM）-1MTPZ（9）式中：P为权重矩阵。

由此可得H（x，y）表达式，分别对其求X，Y方向偏导，结合节点对应的渗透系数可得到节点i处的地下水渗流速度。所取节点越多，曲面越平滑，拟合效果越好。选取“刺状体”表示水流向量，以颜色表示流速大小，将向量长度设为定值，得到水流体单元在X和Y方向上的分量，将其导入3D GIS平台实现可视化。

3 应用实例

3.1 模拟系统开发

集成以上核心算法，开发孔隙地下水系统三维数值模拟与可视化平台。系统分为数据存储层、数据访问层和应用系统层：基于Oracle 11g和ArcGIS SDE引擎实现空间数据和属性数据的一体化建库与管理；利用C++语言搭建系统框架，实现数据库的查询与更新；将OpenGL作为三维场景的渲染引擎，实现数值模拟的可视化管理。

3.2 模拟系统输出结果

以江苏省盐城市第uI承压含水层中地下水数值模拟为例进行验证。根据收集到的水位数据以“月”为单位的特点，设模拟起始时间为2014年10月15日，模拟时间步长30d，利用该系统推算4个时段（120d）内的水位变化情况，经过数次参数拟合，代入系统中进行计算，输出计算结果。研究区15个地下水水位监测井节点的实测与模拟计算结果见表2，可以看出，计算最大误差为1.96m，最小误差为0.01m。

3.3 模拟结果精度分析

由表2输出结果可以看出，在模拟的初始时段（10月），模拟误差绝对值的平均值为0.013m，第3模拟时段的误差约为1.213m，随着时段的推移，模拟误差呈逐渐增大趋势。计算水位最大误差为1.96m，出现在第3个时段。

3.4 预测结果三维可视化

读取离散格网节点不同时段的水位数据，计算地下水渗流速度，对模拟区域内地下水流场、含水层静态模型和水位DEM进行集成显示。不同模拟时段，第Ⅲ承压含水层地下水水位DEM以及流场在空间的分布情况见图9、图10，可以看出，该模型实现了地下水数值模拟计算结果的可视化。

4 结语

结合有限元数值计算原理和承压地下水含水层水文地质特征，研究了3D GIS环境下有限元数值模拟的关键技术与实现方法，并提出了基于3D GIS的地下水流有限元数值模拟技术框架。对现有地下水数值模拟模型的改进主要体现在以下三个方面。

（1）基于三维水文地质建模与分析技术辅助构建水文地质概念模型，可以反映三维孔隙地下水系统在三维空间上的连续分布特征，从而为概念模型构建及其空间分析提供可视化工具。

（2）地下水流有限元计算所用的空间离散格网单元尺寸一般要求能够与水力梯度相适应，通过建立映射函数，将水力梯度映射到单元尺寸上，并结合AFT算法，提出了随水力梯度自适应空间离散格网的自动生成机制。应用实例表明该格网能够自适应反映研究区内水力梯度的空间分布，并有效支持有限元计算。

（3）针对模拟模型计算参数空间分布特征，将其划分为“点、线、面”三种矢量数据类型，并提出了每种数据类型参数的可视化提取与赋值方法。实现了具有较强空间特性的参数数据的高效组织、管理存储与可视化，避免了繁琐参数数据文件的组织与管理工作。

此外，完成了动态自适应的地下水自动模拟系统框架。针对松散沉积含水层空间分布特点，基于GTP空间数据模型实现地下水系统自适应三维动态建模。引入AFT算法对动态建模过程中可能遇到的前沿边的几何形态类型进行分类和归纳，提出改进AFT的自适应格网构建方法。在此基础上梳理了地下水渗流运动的有限元数值求解步骤，研究了利用GIS实现各种类型参数数据管理与组织的方法，解决了地下水渗流数值模拟过程模型参数数据管理不便、效率较低的问题，为三维水文地质动态建模及有限元数据模拟提供了高效、灵活、直观的数据管理模式与平台。但仍存在如下不足之处：将离散格网单元尺寸和水力梯度之间关系近似为简单的线性反比例关系得到二者之间映射关系模型，顾及影响因素较少，有待细化；采用“刺状体”绘制点箭头的方式对地下水流空间分布特征进行建模，当采样点较为密集时，容易引发视觉上的混乱，而采样不足又可能导致关键特征的丢失，难以全面、连续地反映向量场。采用流线法、数值积分法、流函数法等，可对上述问题进行修正，基于不同方法实现地下水流场的三维可视化是后续研究的一个重要方向。