变形监测点位测量精度研究

田正华 刘舜 赵永波

摘 要：本文基于全站仪，应用直接测量模型、交会测量模型、对某一变形点位进行观测。分析、研究不同观测方法所得数据资料的质量和精度情况，并讨论数据资料中观测误差的主要来源。最后比较两种不同观测方法的优、缺点，综合评判后找出最佳观测方法，可为以后类似的测量工作提供一定的经验和依据。

关键词：变形监测；前方交会；粗差识别；平差；误差来源

中图分类号：U456.3 文献标识码：A 文章编号：1003-5168（2018）04-0010-05

Research on Measurement Precision of Deformation Monitoring Poin

TIAN Zhenghua1 LIU Shun1 ZHAO Yongbo2

（1.Department of Surveying and Mapping， Shaanxi Railway Institute，Weinan Shaanxi 714000；

2.China Construction Seventh Engineering Division.Corp.LTD，Zhengzhou Henan 450000）

Abstract： This paper based on the total station and used the direct measurement model， the intersection measurement model and the observation of a certain deformed point position. The quality and accuracy of data obtained from different observation methods were analyzed and studied， and the main sources of observation errors in the data were discussed. Finally， we compared the advantages and disadvantages of two different observation methods， and found out the best observation method after comprehensive evaluation， which will provide some experience and basis for similar measurement work in the future.

Keywords： deformation monitoring；forward rendezvous；gross error recognition；adjustment；source of error

受數据处理方法、实验仪器、大气折光、温度和湿度等外界条件的影响，变形监测获取的数据资料都存在观测误差[1]。因此，应用科学的方法对原始资料进行审查、分类和检验，使之系统化和条理化，确保资料的正确性与可靠性，是为了最后得到正确结果不可或缺的一项工作[2]。

1 常规变形监测数据采集模型

1.1 直接测量法

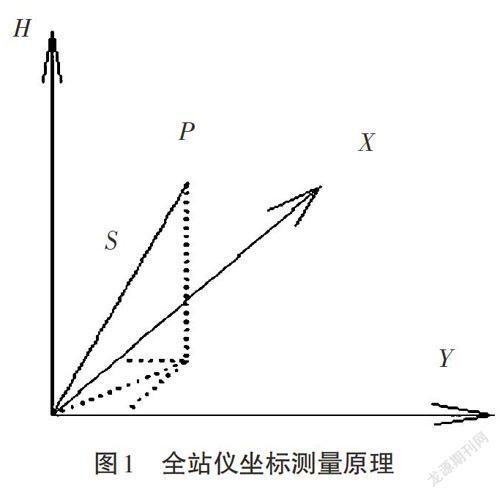
将全站仪架设在已知控制点上，对中整平。然后量取仪高和后视点棱镜高（估读到mm位）并记录，输入记录的数据、测站点及后视点的坐标。瞄准待测变形点，测量待测点的水平角、垂直角、距离，利用这些数据得到待测变形点的三维坐标。原理如图1所示。

由于采用人工测量，因此，在测量仪器高、棱镜高和瞄准时会产生偏差，而且受大气折光的影响，也会影响目标对准。

1.2 交会测量模型

交会法是以2个及以上已知控制点的坐标为基础，使已知点和变形监测点构成一个闭合多边形（一般为三角网形），通过测定三角网中的各边边长或各个内角大小（一般为水平夹角），根据相关公式和定理推导出待测点坐标的一种常用监测技术。交会法示意图如图2所示。

1.2.1 角度前方交会。图3为角度前方交会法示意图。其原理是：A、B两个点为已知点（工作基点），P点为变形点，全站仪测得两水平夹角分别为α和β。已知三角形内角和为180°，因此可以算出AP、PB两边的夹角γ：

[γ=180°-α-β] （1）

由正弦定理可以算出A、P两点之间的距离SAP：

[γSAB=βSAP] （2）

由坐标反算，可以算出AB的方位角[αAB]：

[αAB=arctanyB-yAxB-xA] （3）

根据[α]的角度和[αAB]，可以算出AP的方位角[αAP]：

[αAP=αAB-α] （4）

最后可以算出变形监测点P的坐标[xP]、[yP]：

[xP=xA+SAP×cosαAPyP=yA+SAP×sin αAP] （5）

对P点进行重复观测，第一期变形观测中两夹角为[α1]和[β1]，求得P点坐标值为（[xP1]，[yP1]）；第二期变形观测中两夹角为[α2]和[β2]，P点的坐标值为（[xP2]，[yP2]）。则根据两期监测所得值，解算出P点的位移：

[ΔxP=xP2-xP1]

[ΔyP=yP2-yP1] （6）

[ΔP=Δx2p+Δy2p]

P点的位移方向[αP]为：

[αP=arctanΔxPΔyP] （7）

1.2.2 测边前方交会。图4为测边交会法[3]示意图，A、B为已知坐标控制点（即基点），观测时可在A、B两点架设南方全站仪，测量出水平距离S1和S2。根据已知点A、B可算出两点间的长度，由于三边边长已知，可根据余弦定理，求得AP、AB的夹角[β1]：

[cosβ1=S21+S2AB-S22S1S2AB] （8）

由坐标反算，可以算出AB得方位角[αAB]：

[αAB=arctanyB-yAxB-xA] （9）

根据[β1]的角度和[αAB]，可以算出AP的方位角[αAP]：

[αAB=αAB-β1] （10）

最后可以算出变形监测点P的坐标[xP]、[yP]：

[xP=xA+S1×cosαAPyP=yA+S1×sinαAP] （11）

2 模型参数的求解途径

为了预防粗差，在分析变形监测数据时，需要对观测数据进行预处理，将粗差剔除。监测资料分析中常用的统计判别方法有三种：格拉布斯（Grubbs）准则、莱茵达（3[σ]）准则、狄克逊（Dixon）准则[4]。下面将以格拉布斯准则和莱茵达准则为例说明粗差剔除的原理。

2.1 格拉布斯准则

格拉布斯准则适用条件是观测数据量较少的情况。为了方便判断观测值是否存在异常，须将观测值按从小到大的顺序统计量[见式（12）]，遵从正态分布。

[x（1）≤x（2）≤…≤x（n）] （12）

然后再根据公式计算格拉布斯统计量，即下侧格拉布斯系数[g（1）]和上侧格拉布斯系数[g（n）]。

[g（1）=x（1）-xS] （13）

[g（n）=x（n）-xS] （14）

公式中，[x]表示观测数据序列的算术平均值，S代表标准偏差。当[g（i）≥T（n，α）]时，就认为这组观测数据[x（i）]含有粗差，应予以剔除。[T（n，α）]是观测次数为n时，置信水平为α时的统计量临界值，由表1查取。

2.2 莱茵达准则

莱茵达准则适用于偶然误差服从正态分布，且观测值不含系统误差的情况。对于观测数据序列[x1，x2，x3，…，xn]，若某个观测值[xi]所对应的剩余残差，则将该观测值判为粗差，应该剔除。莱茵达准则是以足够的观测次数作为前提条件的，实际测量中常用贝赛公式算得的标准偏差S代替误差[σ]，对于某个存在问题的数据，若[xi]满足以下公式：

[Vi=xi-x>3S] （15）

[x=1ni=1nxi] （16）

[S=i=1n（xi-x）n-1] （17）

则[xi]含有粗差，对于偏差大于3S的部分观测值，应予以剔除。因为莱茵达法则以观测次数足够多为前提，因此，当n<10时，不宜使用莱茵达准则。

3 精度分析

3.1 三角高程测量的精度

三角高程测量中[5]，竖直观测角为α，A、B间水平距离为D，在不考虑目标高和仪器高的情况下，A、B两点间高差的计算公式为：

[h=D×tanα] （18）

设D和α的中误差分布为[σD]和[σα]，则可得：

[dh=tandDD×sec2αdαρ] （19）

所以可得：

[σ2h=tan2α×σ2D+D2×sec4α×σ″2αρ2] （20）

在实际应用时，由于距离D的误差远远小于垂直角α的误差，所以第一项可以忽略不计；一般来說，垂直角α小于5°，可以认为secα≈1，故得：

[σ2h=（σ″αρ）2×D2] （21）

所以得到三角高程测量中高程的误差公式为：

[σh=σαρ×D] （22）

3.2 边角前方交会的精度

设角[α、β]对应边分别为a（SBP）、b（SAP），则交会角[γ=180°-α-β]，由误差传播定律和相关公式可以得到P点横、纵坐标中误差为[6]：

[mx=mρa2×cos2αAP+b2×cos2αBPsinγ] （23）

[my=mρa2×sin2αAP+b2×sin2αBPsinγ] （24）

P点点位中误差为：

[MP=m2x+m2y=mρ×a2+b2sinγ ] （25）

4 工程实例

已知控制点A的坐标为（61 412.325，64 145.348，272.483）。可以将A点的X值和Y值视为0，高程值H不变，即得到新的A点的坐标（0，0，272.483），在附近区域找一个能够通视的点B，将点A、B的连线作为X轴，过A点的垂线作为Y轴。

在A点架设好全站仪，B点假设立好棱镜（本次实验中使用强制对中杆，便于更好的对中），分别测出A、B两点之间的高差值H和平距值S，进行多次观测，获取的数据结果如表2所示。

获取测量数据后，首先需要对获取的数据进行预处理，即剔除粗差。由于观测数据较少，因此，应该采用格拉布斯准则作为检测方法，以高差值H来进行检验，步骤如下：①将4组观测值从小到大排列，即0.001 4<0.001 5<0.001 6<0.007 5；②求出标准偏差S，由公式计算出S≈30；③根据公式求得各观测值的格拉布斯系数：[g（1）=0.533]，[g（2）=0.533]，[g（3）=0.466]，[g（4）=1.500]；④取置信水平[α=0.05]，由表1可知[Tn，α=T（0，0.05）=1.463]；⑤经过比较各系数可以发现，[g（4）=1.500>T（4，0.05）=1.463]，则认为第三次观测值中含有粗差，应该将其剔除。

粗差产生的原因可能是在观测过程中不小心触碰到了全站仪，使其产生微小移动；或者瞄准棱镜中心时受到强烈阳光的影响使偏差过大。因此，以1、2、4这3次测量的观测值取平均值，得到B点坐标（18.002 4，0，272.484 5）。

通过上述方法，便得到了2个工作基点A（0，0，272.483），B（18.002 4，0，272.484 5）。然后确定一个合适的未知点P，作为变形监测点点位。采用直接测量法获取的P点坐标值如下，一共进行了四次观测，观测结果如表3所示。

经过数据分析，认为这四组观测数据中没有出现粗差。为了提高成果精度，可以取其观测平均值作为P点坐标（10.125 6，10.626 7，272.623 4）。

采用边角交会测量法求得的各项数据如表4所示，该方法同时测量了三角网的内角和边长。其中，α为边AB、AP两条边所形成的水平角，β为AB、BP两条边形成的水平角。

根据表4中所得到的观测数据（α，β，SAP，SBP）和已知点坐标，即A点和B点坐标，使用间接平差计算P点的水平方向位移坐标[7]。可以用Excel表格进行间接平差计算，所得结果如表5所示。

对这4组坐标平差值进行分析后，认为不存在粗差，取其平均值作为P点水平方向上的坐标值（10.125 1，10.627 4）。

采用三角高程测量来获取变形监测点P的垂直方向位移。将全站仪假设在B点，P点假设棱镜。量取全站仪高1.572m和棱镜高为1.400m，测得数据如表6所示。

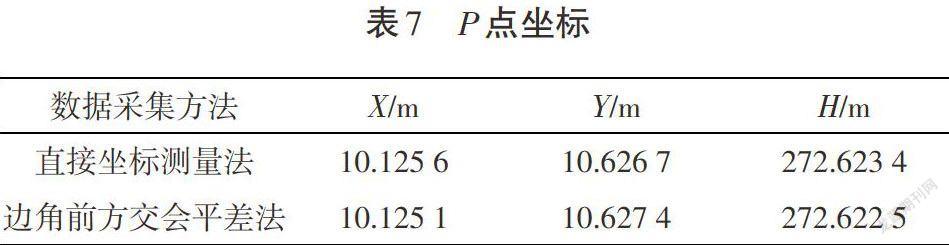
经过数据分析认为，观测值中不含粗差，可以直接进行计算。由第一组观测数据求得HBP=0.138 0；第二组数据求得HBP=0.137 6 ；第三组求得HBP=0.138 5；第四组求得HBP=0.137 7。取4组高差的平均值，可以得到HBP=0.138 0。又已知B点高程为272.484 5m，因此得到P点高程值为272.622 5m。综上所述，由直接坐标测量法和边角前方交会法平差计算后得到的P点三维坐标如表7所示。

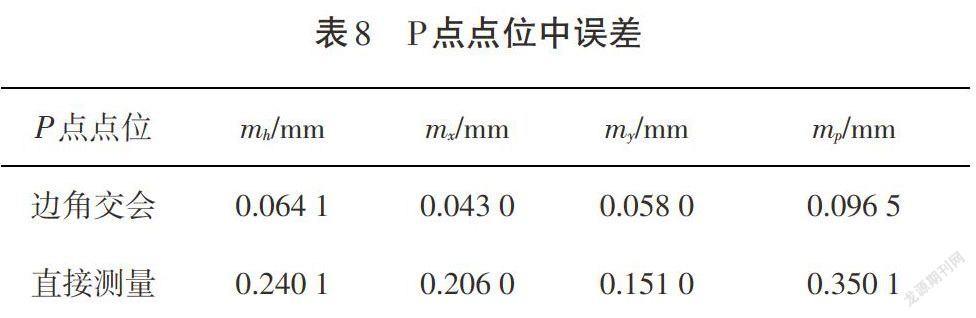
由已知条件可以计算出由边角交会法所测数据求得的P点点位中误差，直接测量法所测坐标的P点点位中误差，如表8所示。

5 结语

本次采集数据主要以直接测量法和交会法为主要研究对象。直接测量法的优点是方法简单，不需要特殊仪器设备，速度快、测量简便，但是结果精度低，且受地形限制大；而交会测量法较前者精度更高，且受外界限制条件少，但是测量过程较为复杂，且需要完成一定工作量的内业数据处理。采用边角前方交会时，构成的三角网较小，边长较短，不能正确地反映出从点位测量精度与边长距离有关的结论。此外，变形观测是针对同一个三角网进行反复观测，而不是重新构造一个新的三角网进行观测，则交会角γ并未改变过。然而，实际情况是γ的大小会影响到监测点位的精度：当交会角较小时，适当增大γ的值可以提高观测精度

参考文献：

[1]许国辉.关于城市建筑变形测量中若干问题的探讨[J].广西大学学报，2003（1）：70-73.

[2]张正禄.工程测量学[M].武汉：武汉大学出版社，2005.

[3]田林亚，周照明，滕松.四种常用坐标测量法的精度对比[J].测绘工程，2009（6）：37-39.

[4]李保平，潘国兵.变形监测[M].成都：西南交通大学出版社，2012.

[5]沈斌，李亚平.高程测量中的误差分析[J].企業标准化，2007（3）：47-48.

[6]武汉测绘学院测量平差组.测量平差[M].北京：测绘出版社，1959.

[7]武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉：武汉大学出版社，2009.