突发水污染风险的马尔科夫链贝叶斯网络预测
2018-09-10靳春玲王运鑫贡力
靳春玲 王运鑫 贡力


摘要:突发水污染事故诱因众多且不确定,为预测此类不确定性因素进而进行防控,提前做好风险预防具有较大的经济意义。通过研究突发水污染事故风险因素、马尔科夫链和贝叶斯网络方法,根据现场调研获取的指标因素,提出马尔科夫链和贝叶斯网络相结合的突发水污染风险预测新方法,从纵、横两方面预测突发水污染事故发生的概率,弥补仅用马尔科夫链不能预测上层指标的不足,并为突发水污染事故的预防提供参考依据。实例分析结果表明:人为因素、机械设备因素和环境因素诱发黄河流域突发水污染事故的概率分别为52%、29%、12%,人为、机械设备和环境三方面应重点关注的风险因素分别是违规操作、管道破裂和自然灾害。
关键词:突发水污染;风险预测;马尔科夫链;贝叶斯网络;黄河流域
中图分类号:X522:TV882.1
文献标志码:A
doi: 10.3969/j.issn.1000-1379.2018.04.015
突发水污染事故具有发生突然、诱因众多、危害严重、处置困难、影响长期等特点,通过统计历史事故,分析水污染事故特征、规律及关键因素,可有针对性地采取措施,降低事故发生率或预防事故发生。近年来,环境和水利工程领域的许多专家分别利用水质模型、多指标综合评价法、AHP(层次分析法)一模糊综合评价法、改进的相对风险模型等方法研究突发水污染风险问题,在风险预测方面集中于对水体中污染物迁移、扩散情况及应急响应时间、水质状况的预测研究,如孟宪林等、蒋新新等采用不同的模型对污染物的动态变化进行预测模拟,陶亚等对事故发生后水厂取水口应急响应时间进行预测,魏智宽等采用灰色模型对突发事故后水质变化进行预测,而对事故风险因素后验概率的预测研究几乎是空白。
研究引发水污染事故的风险因素、分析底层因素导致风险发生的概率及各因素间关系,并预测各上层指标的概率分布,是突发水污染风险预测研究的主要内容。马尔科夫链是一种研究随机问题的预测方法,具有较高的预测精度:贝叶斯网络是概率论与图形理论结合起来表达和推理计算不确定概率性事物的网络结构,广泛用于人工智能、诊断分析、数据挖掘等领域。本研究对马尔科夫链和贝叶斯网络方法进行融合,摒弃马尔科夫链不能分析风险原因和贝叶斯网络预测能力差的不足,充分利用二者的优势,提出了从纵、横两方面进行突发水污染风险预测的新方法,并进行了案例验证和推理。
1 研究方法
1.1 马尔科夫链预测
一般情况下,在当前状态(in)已知的条件下,将来的状态(in+1)可能与过去的状态i0,i1,…,in-1)有关,也可能無关。对随机过程{Xn|n∈T;i0,i1,…,in∈I},若条件概率满足关系式P{Xn+1=in+1|X0=i0,X1=i1,…,Xn=in}=P{Xn+1=in+1|Xn=in},即与过去状态无关,则称随机过程{Xn|n∈T}为马尔科夫链,并将上述特性称为马氏性或无后效性。在马尔科夫链预测模型中,转移概率决定着马氏链的统计规律,对任意的n∈T和状态i∈I、j∈I,称Pij(n)=P(Xn+1=j|xn=i)为马尔科夫链的转移概率。
应用马尔科夫链预测模型的前提条件是随机过程具有马氏性,通常用统计量X2来检验随机序列是否具有马氏性X2的计算公式为式中:fij为状态i转移到状态j的次数;Pj为(fij)n×n的第J列之和同各行各列总和的比值,即PJ=pij为状态i转移到状态j的概率,即
选择置信度χ,查X2分布概率表得X2χ[(n-1)2]。若X2>X2[(n-1)2],则随机过程{Xn|n∈T}具有马氏性。
采用马尔科夫链预测的步骤:①划分状态:②计算每个指标的状态转移概率矩阵:③检验初始数据序列是否具有马氏性,若有则继续下一步,若无则去除该指标因素;④选取初始状态进行预测;⑤结果分析。
1.2 贝叶斯网络
贝叶斯网络(Bayesian Networks,BN)又称信度网络或因果网络,是为解决概率论中联合概率计算问题而产生的,是描述数据变量之间依赖关系的一种图形模型,也是一种用来进行推理的模型。采用框架结构来表示因果关系,逻辑清晰,便于人们理解变量间的复杂关系,常用于不确定环境建模和推理。
贝叶斯网络就是一个有向无环图和模型参数的集合,信息表达由两部分组成:一是网络结构(有向无环图)。网络中的每个节点代表一个变量,节点间的有向弧表示二者因果关系,由起因节点指向结果节点,体现了领域知识的定性特征:二是网络参数(条件概率分布表),体现领域知识的定量特征。在概率推理中,用随机变量代表事件或事物,通过将随机变量转化成各种实例,就可以将一系列事件或事物的现有状态模型化。
贝叶斯网络预测的步骤:①确定网络节点及值域:②建立网络结构:③设置预测条件概率:④贝叶斯网络推理预测。
1.3 马尔科夫链和贝叶斯网络的融合
马尔科夫链是一种依据已知数据样本来探索变量未来状态的纵向预测方法,贝叶斯网络则是一种依据时间序列信息来展示指标因子间相互影响关系的横向预测方法。融合这两种方法,可以预测指标体系中各节点事件的后验概率,以实现对事物风险的宏观、全面和定量预测,为风险决策者提供有效的决策依据。二者的融合,不仅突出动态层次结构,还能够更有效地利用动态时序信息。
马尔科夫链和贝叶斯网络融合的预测步骤:①建立贝叶斯网络模型:②分析指标因素并获取数据,检验数据序列是否具有马氏性,若有则继续下一步,若无则筛除该指标因素:③利用马尔科夫链对底层指标进行预测:④将马尔科夫链预测结果作为证据输入贝叶斯网络模型;⑤用贝叶斯网络推理对上层指标进行预测。
2 突发水污染事故风险预测实例
2.1 建立贝叶斯网络结构
2.1.1 确定网络节点
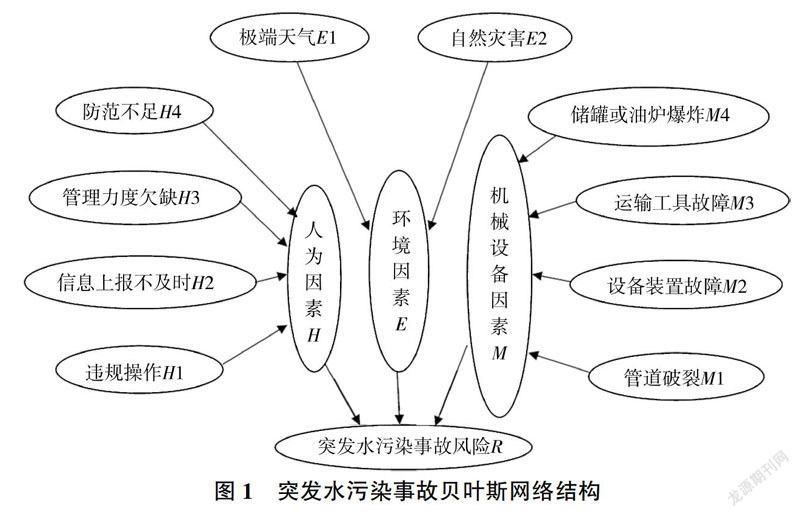
从人为因素、机械设备因素和环境因素三方面分析导致突发水污染事故的原因,经过多次筛选,最终确定14个网络节点,见表1。
2.1.2 建立网络结构
通过分析每一起突发水污染事故发生的因果,综合所有事故样本的因果链,建立图1所示的流域突发水污染事故贝叶斯网络结构。
2.2 数据来源
突发水污染事故一旦发生就会造成巨大损失,但通常不易发生,因此将其视为布尔变量,即变量取值为0和10表示不发生或没发生,1表示发生。本研究主要依托“流域突发水污染风险分区分级方法研究”课题,对《黄河突发水污染事件调查研究报告》中的84起黄河突发水污染事故(见表2)进行分析。
2.3 马尔科夫链预测
2.3.1 马氏性检验
依据表2,构造各指标的概率转移矩阵:式中:Pij=fij/fi,fi为状态i出现的总次数,fij为状态i转移到状态j的次数。
采用式(1)计算可得:X2(Hl)=6.904,X2(H2)=0.240,X2(H3)=12.224,X2(H4)=2.980,X2(Ml)=4.316,X2(M2)=14.268,X2(M3)=2.840,X2(M4)=2.840,X2(El)=4.364,X2(E2)=3.036。
取显著性水平χ=0.1,则x20.1[(2—1)2]=X20.1(1)=2.710。除指标“信息上报不及时H2”外,所有指标的X2值都大于2.710,即除H2外其余指标都具有马氏性,可进行马尔科夫链预测。
2.3.2 马尔科夫链预测
所有具有马氏性的变量的状态可用矩阵形式表示,即发生=[10]、不发生=[01]。据相关研究20,三步预测结果精度高、误差小,所以采用三步预测。记初始状态矩阵为N,转移矩阵为P,则三步预测公式为
M预测=N初始P3
(2)
选取2012年的状态作为初始状態,预测2015年突发水污染事故发生概率,结果见表3。由表3可知,马尔科夫链预测结果与实际情况吻合程度较高,故其可作为初始证据用于贝叶斯网络推理。
2.4 贝叶斯网络预测
贝叶斯网络具有概率的传播性,若初始条件概率已知,则可得到各个节点的概率。本文采用genie软件将表3中马尔科夫链预测的2015年的根节点状态概率作为证据输入到已设置参数的贝叶斯网络模型,得到2015年的各上层指标的风险概率(即各节点的后验概率)条形图,见图2。由图2可知,黄河流域突发水污染事故发生概率为68%,人为因素造成突发水污染事故的概率为52%,机械设备因素造成突发水污染事故的概率为29%,环境因素导致突发水污染事故的概率为12%。
2.5 结果分析
根据图2,逆向推理便可得出贝叶斯网络结构中人为、机械设备和环境这三方面因素各自的薄弱环节,对薄弱环节应重点控制。“人为因素H”节点有违规操作H、管理力度欠缺H3和防范不足H4三个父节点,后验概率依次为42%、12%和11%,控制措施先后次序为Hl、H3、H4。“机械设备因素M”节点有管道破裂Ml、设备装置故障M2、运输T具故障M3和储罐或油炉爆炸M4四个父节点,后验概率依次为17%、13%、3%和3%,控制措施先后次序为Ml、M2、M3和M4。“环境因素E”节点有极端天气El、自然灾害E2两个父节点,后验概率依次为2%、11%,控制措施先后次序为E2、El。
3 结论
将马尔科夫链和贝叶斯网络预测方法融合并应用于突发水污染事故风险因子概率预测,得出如下结论。
(1)二者融合的预测新方法充分体现了马尔科夫链纵向预测底层指标状态的准确性和贝叶斯网络横向预测上层指标后验概率的优点,克服了突发水污染事故指标体系中因上层指标数据缺乏而不能预测的问题。
(2)人为因素是导致黄河流域突发水污染事故发生的最主要因素,诱发概率为52%;机械设备因素是次要因素,诱发概率为29%:环境因素诱发概率为12%。确定的各类底层指标因素预控措施的优先次序,可作为突发水污染事故防制和控制的参考依据。
(3)在大样本数据下,马尔科夫一贝叶斯网络模型能充分挖掘数据信息并准确分析事由。本研究样本欠缺,致使某些指标不具备马氏性及事故风险因素概率分布的准确度可能不高,但为突发水污染事故的风险分析提供了新方法。未来研究中,应增加样本数,以提高风险预测的准确性。
