模拟降雨下流域不同地貌单元形态演变特征

王玲玲 左仲国 孙维营 孙娟 侯欣欣

摘 要：利用室内小流域概化模型和人工模拟降雨试验，分析了在60、90、120、150 mm/h降雨强度下概化流域内支沟和全流域等不同地貌单元形态演变特征。结果表明：随着模拟降雨场次增加和降雨强度的增大，地貌分形信息维数呈明显的增大趋势，各支沟和全流域沟网不断发育，各地貌单元的地貌形态逐渐复杂，而且支沟和全流域地貌形态变化过程呈现出不同的阶段性，支沟地貌形态变化較全流域更为剧烈：随降雨强度增大和降雨场次的增加，支沟和全流域等地貌单元地貌信息熵单调增大，且支沟沟网起伏程度大于全流域，随着空间尺度增大，地貌形态演变剧烈程度有所降低。

关键词：地貌分形信息维数：地貌信息熵：地貌形态：地貌单元：地貌演变特征

中图分类号：S157.1

文献标志码：A

doi： 10.3969/j.issn.1000-1379.2018.06.022

黄土丘陵沟壑区地貌具有明显的垂直分带性，从分水岭至坡脚可划分为梁峁坡和沟坡，梁峁坡和沟坡连接的整体称为坡沟系统，坡沟系统组成流域最基本的集水区，不同级别的集水区组成流域的毛沟、支沟和干沟等不同空间尺度地貌单元，不同空间尺度地貌单元水沙输移过程、水沙关系呈现出显著的差异性[1-5]。流域水沙输移过程不仅受降雨径流动力条件的影响，还受下垫面条件的影响。地貌形态是反映流域下垫面条件的重要参数之一，地貌形态量化是研究侵蚀空间尺度效应的重要内容[6]。流域地貌形态量化参数经历了从传统的单因子参数（如平均坡度、平均坡长、沟壑密度、流域高差比和切割深度等）[7-8]到以分形几何为代表的非线性量化参数的发展过程[9-11]。传统的单因子参数无法准确描述和刻画流域的三维立体形态，分形理论的建立为流域地貌形态特征的定量描述开辟了新的思路[12]。流域沟网的发育过程对应着系统的熵增过程，从系统熵增的程度可以判断流域沟网的发育程度，作为判断流域地貌演化阶段的量化指标之一。

鉴于此，笔者采用小流域概化模型和人工模拟降雨试验相结合的办法，以地貌分形信息维数和地貌信息熵为量化参数，研究流域不同空间尺度地貌单元地貌演变特征，以期为揭示土壤侵蚀尺度效应提供理论支撑。

1 材料与方法

1.1 模型制作

试验在水利部黄土高原水土流失过程与控制重点实验室试验大厅进行。以黄土丘陵沟壑区桥沟流域为原型，基于降雨相似性[13]、土壤特性相似[14]和侵蚀产沙过程相似，在对原型流域地貌形态特征统计分析的基础上，设计具有初步沟网的室内小流域概化模型。概化小流域模型初始地貌形态特征见表1。

试验用土取白郑州邙山，模型基础装土1m厚不过筛，并灌水自然压实，防止试验过程中发生沉降。表层土壤先过1 cm筛去除杂物，然后分层填充，供试土样粒径级配见表2。模型填土制作完成后，经过洒水和约3个月时间的自然沉降压实，经测定，表层土壤干容重与自然修复流域地表土壤干容重接近，控制在1.4～1.5 g/cm。

1.2 观测设备安装

概化模型上方安装下喷式降雨器，依据黄土高原侵蚀性降雨特征研究成果，模拟雨强为60、90、120、150 mm/h，相应降雨历时分别为60、45、45、45 min。下喷式降雨器下方垂直悬挂三维激光扫描仪（型号为FARO）。流域模型及观测设施布设平面及断面见图1。

1.3 地貌形态采集

在每一次降雨开始前和结束后，打开悬挂在降雨器下方的三维激光扫描仪，分别扫描降雨前后概化流域地貌形态，将概化小流域形态扫描为点云数据，在Arc GIS平台下对扫描的点云数据进行处理，并建立相应地貌单元DEM模型，提取流域等高线和流域沟网，对降雨前后地形数据进行对比分析，确定在降雨条件下概化小流域地貌形态变化特征，前一场降雨后的地貌形态可作为下一次降雨前的初始地貌形态。

1.4 研究方法

1.4.1 地貌分形信息维数计算

分形维数是对复杂形体不规则性量度的重要参数，可用盒维数描述河网类的分形现象[15]。按照Mandelbrot的定义[16]，分形分布满足如下关系式：式中：N，（F）为与研究对象相交的盒子数。

盒维数也可表述为In N，（ F）相对于- In r的斜率。基于沟网形态的地貌形态分形维数计算过程如下。

（1）流域沟网提取。以流域DEM为基础数据源，在ArcGIS平台完成。提取步骤见图2，提取的不同场次降雨下沟网形态见图3。

（2）基于覆盖法的分维估算。在Arc：GIS中利用创建渔网（ Fishnet）命令生成大小分别为10 mm×10mm、20 mm×20 mm、……、500 mm×500 mm的网格，然后将这些网格分别覆盖不同地貌单元沟网，利用Arc GIS的属性查询功能统计得到非空网格数，第一期扫描数据计算结果见表3。

（3）建立沟网形态分维关系。以In r为横坐标、In N（r）为纵坐标，将表3中的计算结果点绘在双对数坐标纸上，利用最小二乘法可拟合出一条直线（见图4）。

拟合的关系式为

In N（r）=一1.121 2 In r+10.653

（3）

根据盒维数计算原理，回归系数即为分形维数。1.4.2地貌信息熵计算

艾南山[17]通过类比信息熵原理，建立了流域侵蚀地貌系统信息熵概念及其表达式：式中：H为地貌信息熵：S为Strahler面积一高程积分值f（x）为Strahler面积一高程曲线。

面积一高程积分值的计算方法为：设A为i流域的总面积，α_im为i流域内第m条等高线以上的面积，h_i为该等高线与i流域最低点的高差，△H_i为i流域最高点与最低点的高差，则以α_im/A_i为y轴，以h_i/AH/_i为x轴，显然x、y均在[0，1]内取值，根据得到的一系列（x，y）值，以x为横坐标、y为纵坐标绘出的曲线即为面积一高程曲线，曲线与坐标轴之间的面积即为面积一高程积分值。

2 结果与分析

2.1 不同地貌单元地貌信息维数变化特征

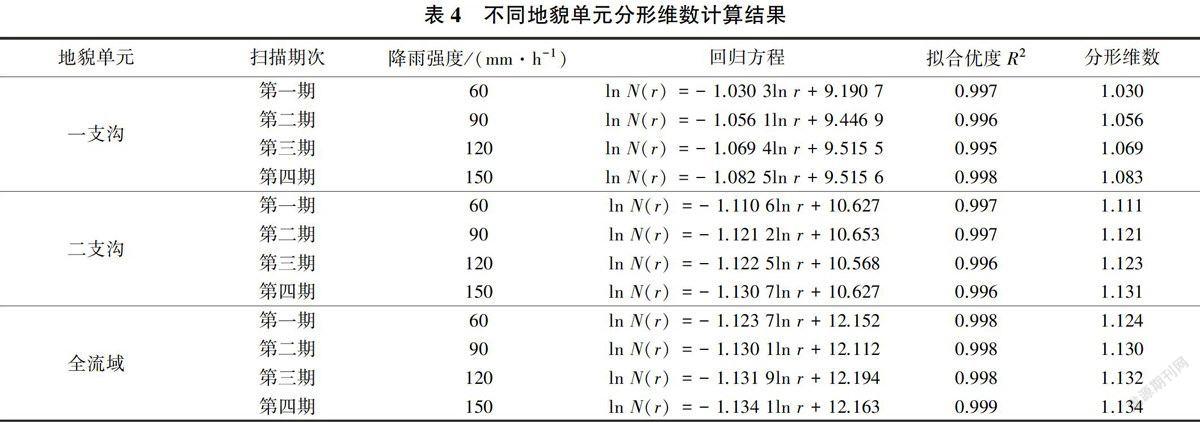
利用上述方法对每期流域模型地貌形态DEM进行分形维数测定，结果见表4。不同空间尺度地貌单元地貌形态分形维数变化情况见图5。

从表4和图5可以看出，随着模拟降雨场次增加和降雨强度的增大，不同单元地貌形态分形维数不断增大，说明在降雨击溅和径流沖刷作用下，不同地貌单元地貌形态逐步趋于复杂化。一支沟地貌分形维数由第一期降雨后的1.030增大至第二期降雨后的1.056，增大了2.50%，随后增大至第三期降雨后的1.069，增大了1.26%，最后达到第四期降雨后的1.083，增大了1.22%：二支沟由第一期降雨后的1.111增大至第二期降雨后的1.121，增大了0.95%，随后增大至第三期降雨后的1.123，增大了0.12%，最后增大到第四期降雨后的1.131，增大了0.73%：全流域由第一期降雨后的1.124增大至第二期降雨后的1.130，增大了0.58%，随后增大至第三期降雨后的1.132，增大了0.16%，最后增大到第四期降雨后的1.134，增大了0.19%。这种变化趋势说明，随着模拟降雨场次增加和强度的增大，小流域模型地貌形态变化呈现显著的非均衡性。

不同空间尺度地貌单元地貌形态变化过程呈现出不同的阶段性，总的来说，随着降雨场次增加和降雨强度增大，支沟地貌形态变化较全流域更为剧烈，其中一支沟地貌形态变化最为剧烈，全流域的地貌形态变化最为缓慢。就各个地貌单元而言，其变化过程表现出不同的阶段性。一支沟分形维数增大最为迅速的为第二期扫描的降雨场次，地貌形态分形维数增大2.50%，为一支沟地貌形态变化的活跃阶段，随后地貌形态变化呈现减缓趋势，此时沟网向纵深发展，并不影响沟网的分形维数变化：二支沟和全流域分形维数增大最为迅速的亦为第二期扫描的降雨场次，地貌分形维数分别增大0.95%和0.58%，此阶段仍是二支沟和全流域地貌形态变化的活跃阶段，之后直至模拟降雨结束，小流域模型地貌分形维数呈现先减小后增大的变化趋势，说明二支沟和主沟的地貌形态仍在不断调整中，未达到相对稳定状态。因此，不同地貌单元空间尺度越大，地貌形态演化达到稳定阶段需要的时间就越长。

2.2 不同地貌单元地貌信息熵变化特征

根据地貌信息熵的计算原理，运用ArcGIS的空间分析功能，在流域内每隔10 mm高程生成一条等高线，将等高线文件与流域边界文件叠加，提取出不同高程以上的面积。按上述方法进行曲线拟合，得到Strahler面积一高程曲线方程，用三次多项式进行拟合，效果较好（ R2 >0.950）。此曲线与坐标轴所包围的面积，即此曲线在一定范围的定积分就是Strahler面积一高程曲线积分值S。表5中列举了不同场次降雨下流域地貌Strahler曲线方程、积分值S和信息熵值H。

流域的相对高度决定流水势能的大小，水流在运动过程中不断将势能转化为动能，成为泥沙起动和搬运的原动力，是流域泥沙侵蚀搬运发生的重要因素。动能公式为式中：E为动能；m为水流质量；v为水流速度。

流域汇水面积所接受的降水量决定了水流的质量，从而决定了水流的动力。因此，对不同地貌单元地貌信息熵的定量计算可以在一定程度上反映不同地貌单元沟网的发育阶段。从不同地貌单元地貌信息熵的计算结果（见表5）来看，不同空间尺度地貌单元地貌信息熵随降雨强度增大和降雨场次的增加而增大，说明模拟雨强增大则侵蚀加剧，流域沟网发育逐渐成熟，符合熵增原理。

不同地貌单元地貌信息熵在相同降雨条件下增大的幅度不同（见图6），当降雨强度从90 mm/h增大到120 mm/h时，地貌信息熵一支沟、二支沟、全流域分别增大21. 41%、11. 82%、1.14%，说明在相同降雨条件下，随着空间尺度的增大，地貌形态演变剧烈程度降低，支沟的沟网起伏程度大于全流域的。和地貌分形维数相似，随着降雨场次的增加，地貌信息熵同样表现出阶段性。就全流域而言，当持续模拟120 mm/h雨强时，地貌信息熵增大幅度最大，为7.67%，是沟网纵深发展最为剧烈的阶段，之后地貌信息熵增大幅度减小：就一支沟和二支沟而言，当降雨强度由90 mm/h增大到120 mm/h时，地貌信息熵增大幅度最大，分别为21.41%和11. 82%，此阶段是一支沟和二支沟沟网纵深发展最为剧烈的阶段，之后随着降雨场次增加和降雨强度的增大，地貌信息熵增大的幅度减小。

艾南山等[18]曾计算过各地区的Strahler积分S值，发现S值的大小与水毁严重程度有一致的变化趋势，S值可以作为区域稳定性的判别标准。从表5可以看出，随着降雨场次增加和降雨强度增大，Strahler积分值S处于不断减小的发展趋势，在一定程度上反映出不同地貌单元沟网不断调整，地貌形态逐渐处于稳定。

3 结语

流域地貌形态是内外营力对抗在某一时刻的瞬时平衡，地貌形态的演化是一个物质传输过程。概化流域模型在降雨径流作用下形成的流域沟网是径流泥沙输送的通道，分形信息维数能够准确地描述沟网的平面复杂程度，可以很好地表达沟网的纵向发展过程。在沟网平面纵向形态不断发展的过程中，沟网的深度也在不断发展，大雨强下的沟网比小雨强的更宽更深，分形信息维数无法反映沟网的深度起伏状况，而地貌信息熵能较好地反映地形起伏的程度。

随着模拟降雨场次增加和降雨强度增大，地貌分形信息维数呈明显增大趋势。不同空间尺度地貌单元地貌形态变化过程呈现出不同的阶段性，支沟地貌形态变化较全流域的更为剧烈。不同空间尺度地貌单元地貌信息熵呈单调增大趋势，支沟沟网起伏程度大于全流域的。

参考文献：

[1]唐政洪，蔡强国，许峰.流域侵蚀产沙的尺度变异规律研究[J].中国水土保持科学，2004，2（1）：56-62.

[2] 倪九派，魏朝富，谢德体.土壤侵蚀定量评价的空间尺度效应[J].生态学报，2005，25（8）：2061-2067.

[3]刘纪根，蔡强国，刘前进，等.流域侵蚀产沙过程随尺度变化规律研究[J].泥沙研究，2005（4）：7-13.

[4] 李秀霞，李天宏.黄河流域泥沙輸移比与流域尺度的关系研究[J].泥沙研究，2011（2）：33-38.

[5] 王玲玲，姚文艺，王义龙，等.黄土丘陵沟壑区多尺度地貌单元输沙能力及水沙关系[J].农业T程学报，2015，31（ 24）：120-126.

[6] 崔灵周，李占斌，郭彦彪，等.基于分形信息维数的流域地貌形态与侵蚀产沙关系[J].土壤学报，2007，44（2）：197-203.

[7] 白战国.地貌条件与土壤侵蚀关系的定量研究：以窟野河流域为例[J].陕西师范大学学报，1992，20（2）：63-66.

[8] 吴普特，周佩华，武春龙，等.坡面细沟侵蚀垂直分布特征研究[J].水土保持研究，1997，4（2）：47-56.

[9]王协康，方绎.流域地貌系统定量研究的新指标[J].山地研究，1998，16（1）：8-12.

[10]朱永清，李占斌，崔灵周.基于GIS地貌形态特征分形信息维数与等高距关系研究[J].水土保持学报，2005，19（1）：105-108.

[11] 张传才，秦奋，汪永新，等.流域地貌形态多尺度三维分形量化及尺度效应：以砒砂岩区二老虎沟为例[J].水土保持研究，2016，23 （1）：278-283.

[12] 张捷，包浩生.分形理论及其在地貌学中的应用：分形地貌学研究综述及展望[J].地理研究，1994，13（3）：104-111.

[13] 雷阿林，唐克丽.土壤侵蚀模型试验中的降雨相似及其实现[J].科学通报，1995，40（ 21）：2004-2006.

[14] 雷阿林，史衍玺，唐克丽.土壤侵蚀模型实验中的土壤相似性问题[J].科学通报，1996，41（ 19）：1801-1804.

[15] 张攀，姚文艺，唐洪武，等.模拟降雨条件下坡面细沟形态演变与量化方法[J].水科学进展，2015，26（1）：51-58.

[16]

MANDELBROT B.How Long is the Coast of Britain？ Sta-tistical Self-Similarity and Fractional Dimension[J].Sci-ence，1967，156（ 3775）：636-638.

[17] 艾南山.侵蚀流域系统的信息熵[J].水土保持学报，1987（2）：1-8.

[18]艾南山，岳天祥.再论流域系统的信息熵[J].水土保持学报，1988（4）：3-11.