动荷载作用下饱和粉土动力特性研究

田竞 杜春雪 王江锋 侯庆雷 郭林芳

摘要：为了分析不同动强度影响因素的动荷载作用下黄河冲洪积粉质土的动应力一动应变发展规律，模拟了一定振动频率的循环荷载的动三轴试验。试验选用郑州市东北部分布广泛的粉土，分析了动应力幅值、循环振动次数、固结围压、固结比等对粉土动力特性的影响，从动应力一动应变关系研究了动荷载作用下粉土的动力特性。试验结果表明：饱和粉土的动应力一动应变的发展与土样的动强度影响因素有关；在循环荷载作用下，因动荷载与围压比值的不同，试样呈现出三种形态；随动荷载作用次数的增加，在同等动应力幅值作用下，试样抵抗外力引起变形的能力越来越差，其弹性模量随振动次数增加而减小、随围压的增加而增大。

关键词：动荷载；动力特性；动三轴试验；饱和粉土

中图分类号：TU411.8； TV16

文献标志码：A

doi：10.3969/j.issn.1000-1379.2018.08.033

粉质土作为黏性土和砂土之间的过渡土类，属于单粒状堆积结构，极易振动液化失水，土层压缩沉降量大，承载力低，具有特殊的工程特性。随着工程建设的广泛开展，土体受到振动作用的荷载越来越多，如波浪荷载、地铁振动荷载、地震荷载、爆破荷载等，在这些动荷载的循环作用下土体易发生变形、破坏，进而导致地基沉陷、构筑物失稳等重大灾害事故的发生。在黄河冲洪积平原一带分布着广泛的粉土沉积层，郑州市东北部的黄河泛滥平原也不例外。

目前，关于动荷载作用下土的动力特性及破坏机理研究成果多以黄土、软黏土和淤泥质黏土为主，对于粉土方面的研究鲜有涉及。有关学者根据动荷载的特点、土质特性，借助室内动三轴试验及数值分析方法，研究了动荷载作用下土的动力行为：张希栋等利用SDT-20型动三轴仪探究了黄土在双向动荷载下的动剪切模量特性：赖夏蕾等借助GDS动三轴仪，分析了不同围压下淤泥质土在循环荷载作用下的动应变、动强度、动剪切模量和阻尼比特性；谢琦峰等以相对动应力来分析不同围压、不同动应力下黏质粉土的累积塑性应变变化规律，并建立了可用于长期振动荷载作用后黏质粉土的孔压计算的经验公式。对不同动强度影响因素的动荷载作用下粉土的动强度变化及变形特征的研究还比较少。基于此，本研究通过现场取样、室内试验及理论分析，研究不同动强度因素作用下土体的动力特性，初步得到动应力一动应变双曲线模型，以期为黄河冲洪积平原的相关工程建设提供参考。

1 试样的制备及试验方案

1.1 土样的选取及试样制备

选取原状粉土样的土层深度为9～16m，现场钻孔取样，取出高度200mm、直径100mm的圆柱形原状样，运输过程尽量避免振动和摇晃，最大限度地减小人为因素的影响。本次试验所用仪器标准试样尺寸为高度80mm、直径39.1mm的圆柱，用切土刀将土样切成略大于标准试样的圆柱，要求同一组土样密度相差不超过0.03g/cm3、含水率相差不超过2%，测得原状土样基本物理指标见表1。

1.2 试验设备

试验采用KTG全自动三轴压缩仪进行原状土在围压100、150、200、250kPa作用下的静三轴试验，轴向应变达5%时判定试样破坏。绘制各围压条件下的应力莫尔圆及圆的公切线（图1），由此计算原状土样在静三轴下的黏聚力c为30kPa、内摩擦角（φ为17°。

1.3 试验方案

影响土动力特性的因素很多，本试验结合动荷载大小、振动频率大小和荷载形式（用正弦波模拟），考虑围压、固结比、动应力幅值等因素来确定试验方案。试验中固结比Kc=1，设定振动次数为1000次，具体试验方案见表2，其中v表示原状样标号。

2 原状土样动三轴试验

2.1 土样破坏形态

通过对试样的试验数据进行分析，y1、y2、y3试样组压缩密实稳定，呈现该种形态试样的共同点是动应力幅值与围压的比值（循环应力比）比较小；y4、y5、y6、y8、y14试样皆出现拉伸型破坏，且基本是靠近试样帽一端被拉伸破坏；y7、yl0、yll、y12、y13试样出现压缩破坏；y9、y15土样发生斜向破坏且轴向应变达5%。三种形态见图2。

2.2 土样强度的影响因素分析

2.2.1 循环振动次数

以原状样y11的振动三轴试验结果为例，分析动荷载作用次数对饱和粉土动力特性的影响。试样的固结围压为200kPa、固结比Kc=1、动应力幅值为90kPa。由图3可见，当振动次数Ⅳ=100、200、300、400时，试样在动荷载作用下的應力一应变曲线都形成了封闭的滞回圈，随振动次数的增加，其横向波形变化越来越大[图3（a）]；随动荷载作用次数的增加，在同等动应力幅值作用下，试样抵抗外力引起变形的能力越来越差，试样的弹性模量随振动次数的增加而减小，试样的阻尼比则随振动次数的增加而增大[图3（b）]。

2.2.2 动应力幅值

选取试验中100kPa围压下三组试样的轴向最大应变来分析动应力幅值对土样强度的影响规律。

由图4可见，动应力幅值对土样应变曲线变化影响较为显著，在一定固结围压条件下，存在一特定的临界循环动应力，当动应力幅值小于临界循环动应力时，如动应力幅值为30、40kPa，最后轴向应变值未达到5%，而是稳定在一个小于5%的数值，符合上述土样的破坏形态（即压缩密实稳定型）：当动应力幅值大于临界动应力时，如动应力幅值为50kPa，在600次振动作用下，其轴向应变达到5%，可以归结为破坏型，振动前期试样的轴向应变随振动次数增加基本上呈线性增长，随着动荷载作用次数的增加，曲线出现拐点（N=300），拐点之后应变基本上呈幂函数型增长。

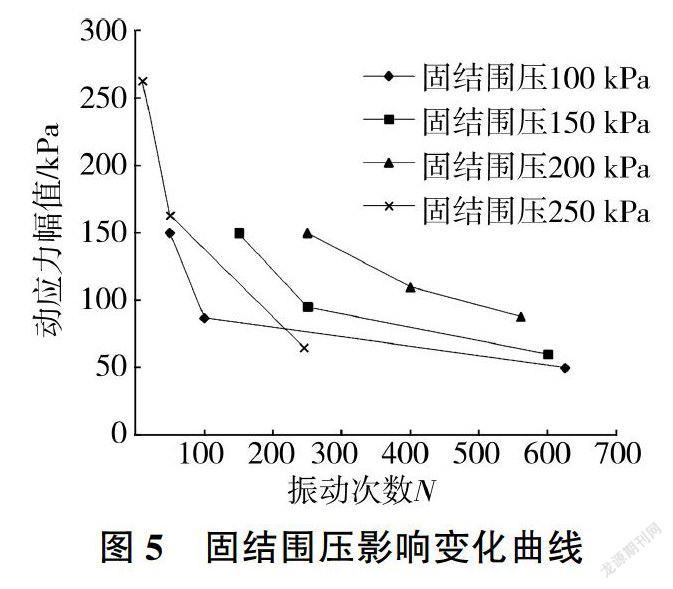
2.2.3 固结围压

由图5可见，在相同的动应力幅值作用下，围压大的试样比围压小的试样动荷载循环振动次数多：固结围压为250kPa时，试样的动强度明显低于小围压的情况，在达到相同的应变破坏标准，动荷载循环次数明显低于较小围压条件下的：围压较小的条件下，原状样因其自身结构性的存在（即长期的天然沉积过程中形成的），试样的应力水平即固结围压未达到结构的屈服条件时，其抗剪强度较大，但随着固结围压的不断增大，土体因其结构性遭到破坏而表现为抗剪强度明显降低。

2.2.4 固结比

选取两组试样，固结围压为1OOkPa、动应力幅值60kPa，设定轴向应变达5%时停止试验，试样轴向应变与振动次数Ⅳ的关系曲线见图6。

由图6可见，在动荷载的循环作用下，轴向应变随振动次数的增加而增大，最后达到应变破坏标准。固结比Kc=1时，轴向应变分三个阶段，开始应变增长速率较快，之后慢慢减小，在振动次数达到20时，曲线出现拐点，之后应变曲线基本上呈线性增长，直至试样达到破坏：固结比Kc=1.5时，应变与振动次数基本上呈线性关系，整个应变时程曲线比较平缓，最后达到应变破坏标准。

3 试验结果与分析

基于上述土样强度的影响因素及对试验结果的分析，选取两组不同围压（100、200kPa）下的三组试样动应力幅值所对应的试验数据，分别确定相同动荷载作用次数的动应力σd和动应变ξd，绘制一定围压、一定振动次数下的动应力一动应变关系曲线。取振动次数Ⅳ=40，不同围压相同动荷载作用次数下原状样的动应力一动应变关系见图7。

由图7可见，曲线（a）中相同动应力幅值下，轴向应变随围压的增大而减小；曲线（b）中1/Ed-ξd（Ed为动弹性模量）近似呈线性变化关系，设其拟合曲线表达式为1/Ed=a+bξd，围压为100、200kPa时相应的拟合式为

当围压为100kPa、ξd=0.65时，根据式（1）求得最大动弹性模量为73kPa；当围压为200kPa、ξd=0.35时，根据式（2）求得最大动弹性模量为236kPa，这与曲线（c）中不同围压所对应的最大动弹性模量相一致，说明曲线（c）的拟合效果较好。同时，根据式（1）、式（2）可求得等压固结条件下，不同围压作用下的最大动弹性模量：在土体结构屈服应力以下，最大动弹性模量随试样围压的增大而增大。

4 结论

以郑州市东北部黄河泛滥平原的原状粉土为研究对象，进行室内振动三轴试验，模拟现场的实际受力情况，结合试验数据，从土样破坏形态、强度影响因素等分析了粉土在动荷载作用下的動力特性。

（1）动三轴试验后试样呈现三种形态：压缩密实稳定、拉伸或压缩破坏以及剪切破坏。

（2）随着动荷载作用次数的增大，试样的轴向应变逐渐增大，动弹性模量逐渐减小，表现为同等动荷载作用下轴向应变越来越大，试样在动荷载作用下的应力一应变曲线所形成的封闭滞回圈也说明了这一点。

（3）原状土样因其自身结构性的存在，其动强度随围压变化存在两种情况：当围压小于结构屈服应力时，试样动强度随围压的增大而变大：当围压大于结构屈服应力时，试样动强度随围压的增大而减小。

（4）原状试样在不同围压、一定振动次数下的动应力一动应变关系曲线符合双曲线模型，可结合拟合公式，求得该条件下的最大动弹性模量。