基于FLOW—3D的水垫塘底板脉动压力数值模拟

唐尧 张根广 程烨

摘要：水垫塘底板作为下游河床的防护结构，承受着高速水流的持续冲击，脉动压力是引起其冲刷破坏的主要因素。基于FLOW-3D软件，采用RNGk-ζ紊流模型和VOF法对某高拱坝水垫塘底板脉动压力进行了数值模拟，得到了动水压力的时均值、脉动压强系数、概率密度分布和功率谱密度。通过物理模型试验结果验证表明，模拟计算值与物理模型实测值吻合较好，说明数值模拟方法可以应用于脉动压力研究。

关键词：脉动压力；水垫塘底板；数值模拟；FLOW-3D

中图分类号：TV653

文献标志码：A

doi：10.3969/j.issn.1000-1379.2018.08.028

我国水电站大都建于高山峡谷地区，具有高水头、大流量、泄洪功率大等泄洪消能特性。工程中一般采用修建二道坝，形成具有一定水深的水垫塘来消能防冲。下泄水流射入水垫塘后，产生巨大的冲击压力，有可能造成水垫塘底板失稳破坏，因此研究水垫塘底板上动水压强的脉动特性具有重要意义。

目前，对脉动压力的研究以物理模型试验为主。廖华胜等对1：100比尺的小湾水垫塘底板脉动压力进行了量测，发现脉动压力互相关系数随水垫深度的增大有所增大，随离冲击区距离的增大呈近似指数衰减。张少济对比分析了透水防护结构与不透水防护结构在底流消能与冲击射流情况下脉动压力幅值特性及频谱特性的沿程分布特征，并研究了系列比尺模型试验中脉动压力的幅值特性及频谱特性的相似律问题。张建民等通过水工模型试验分析了失稳区底板块动水压力特性及相关特性，发现水垫深度是影响底板所受脉压幅值和相关特性的最主要因素。邓军等研究了掺气对水垫塘及冲坑底部压力特性的影响，结果表明掺气使平底水垫塘底板上射流冲击区的脉动压力增大。

虽然脉动压力在模型试验方面已经取得了较多的成果，但由于模型试验周期长、成本高，同时受到模型比尺相似律问题的影响，因此脉动压力研究受到一定限制。数值模拟作为一种可以对各种复杂物理条件下流场实现全域模拟并提供丰富信息的研究方法，能够极大地增强研究者解决复杂问题的能力。近年来，数值模拟方法已被，一泛应用于水力机械内部脉动压力的相关研究，并取得了良好的效果。而将数值模拟方法应用于高坝泄流时水垫塘底板脉动压力研究的相关文献和报道很少。为了探究数值模拟应用于水垫塘底板脉动压力研究的可行性，笔者基于FLOW-3D软件，对某高拱坝水垫塘脉动压力进行了三维数值模拟，并结合物理模型试验对模拟计算结果进行了验证。

1 物理模型试验简介

某高拱坝位于陕西省汉中市佛坪县与安康市宁陕县交界的子午河中游峡谷段。大坝为碾压混凝土双曲拱坝，最大坝高145m，坝顶高程646m。大坝按500a一遇洪水标准设计，按2000a一遇洪水标准校核。泄洪建筑物为2级建筑物，由坝身泄洪表孔、泄洪底孔及下游消能防冲建筑物等组成。泄洪表孔采用浅孔布置形式，泄洪底孔相间布置在3个表孔之间，形成“三表孔两底孔”的布置格局。表孔堰顶高程628m，孔口尺寸15mx15m（宽×高）。底孔底板高程550m，进口设置垂直平板检修闸门，孔口尺寸4mx6m（宽×高）；出口设置弧形工作闸门，孔口尺寸4mx5m（宽×高）。泄洪建筑物均采用挑流方式消能，并在下游设置消力池。消力池底宽70m、长200m，采用混凝土底板衬砌，底板高程514m。

物理模型按照重力相似准则进行设计，模型比尺为1：60，模拟了坝轴线以上298m的库区、坝轴线以下587m的河道。

在物理模型试验中，点脉动压力采用宝鸡市秦岭传感器厂生产的单晶固态硅片压阻式传感器测量，数据监测采集采用成都泰斯特公司生产的动态信号采集设备（TST5103-V）。根据水垫塘底板动水压力测量结果，分别在水垫塘底板上布置若干个脉动压力传感器，1～7号测点布置位置如图1所示。

根据恩奎斯定理，对于频带宽度为A（Hz）的随机信号，采样频率f≥2A。前人研究表明，水垫塘底板脉动压力的主频A集中于0～10Hz，因此模型试验脉动压力采样频率取32Hz。相应的采样时间间隔t=0.03125s，采样总历时180s，采样容量Ⅳ=5760。

2 数学模型及边界

2.1 数学模型

由于RNGk-ζ紊流模型比标准k-ζ紊流模型能够更好地处理高应变率及流线较大弯曲的流动，因此采用RNGk-ζ紊流模型对水垫塘内水流进行数值模拟。采用VOF方法追踪模拟自由水面。在水气两相流中，定义函数χw和χa分别代表计算区域内水和气占计算单元的体积分数。在每个单元中，水和气的体积分数之和为1，即χw+χa=1oχw表示该计算单元内全部充满水，χw=0表示该计算单元内全部充满空气，O<χw<1表示该计算单元内既有水又有空气。

2.2 计算域网格划分及边界条件处理

基于FLOW-3D软件，数值模拟计算按照原型尺寸建立几何实体模型。计算范围：上游库区长200m、宽120m，坝体、表孔及水垫塘。模型划分网格数量为1800万个左有，设置两个网格块，其中网格块1尺寸为0.8m，网格块2为嵌套加密网格，网格尺寸为0.4m。

上游水流进口采用压力边界条件，出口采用自然出流边界条件，与大气相通的边界采用压力边界条件。固体壁面采用无滑移边界，近壁面采用标准壁面函数法处理，固体壁面粗糙率设为0.0014m。为了缩短计算时间，加快稳定速度，初始化设置时，在上游库区和下游水垫塘内预加水体，上游库区预设水位为642.0m，水垫塘内预设水位为533.0m。

3 计算与试验验证

3.1 时均压力及脉动压强系数

选取上游库水位642.0m、中表孔单开及下泄流量为1615m3/S的工况作为计算工况。在水垫塘内流场达到稳定后，开始采集压力数据，采样结果见表1。

由表1可见，模拟值与实测值吻合较好。时均压力最大绝对误差为-16.97kPa，最大相对误差为6.34%：脉动压强系数最大绝对误差为-9.78kPa，最大相对误差为12.96%。大多数测点相对误差绝对值在7%以内，表明采用RNGk-ζ紊流模型对水垫塘内水流脈动压力进行数值模拟是可行的。

3.2 脉动压力概率密度分布

脉动压力概率密度分布是否符合正态分布一般采用序列的偏态系数和峰态系数来验证。

偏态系数Cs用来表示分布的对称性，峰态系数CE用来表示峰值的高低和标准情况的偏离程度，对于标准正态分布，Cs=0、CE=3。图2、图3是2个典型测点处脉动压力概率密度分布图，横坐标为瞬时压力p减去时均压力p的脉动值，纵坐标为瞬时值所对应的概率密度。

可以看出，脉动压力实测值与模拟值的概率分布基本相同，即脉动压力集中分布在时均压力值附近，没有出现较大的偏离。各测点实测值的偏态系数为1.70～2.17，峰态系数为4.62～11.24：模拟值的偏态系数为1.57～2.08，峰态系数为5.86～10.04。偏态系数>0说明出现正向脉动概率大于出现负向脉动的概率，峰态系数>3说明脉动压力具有间歇性且分布较为集中。

3.3 脉动压力的频谱分析

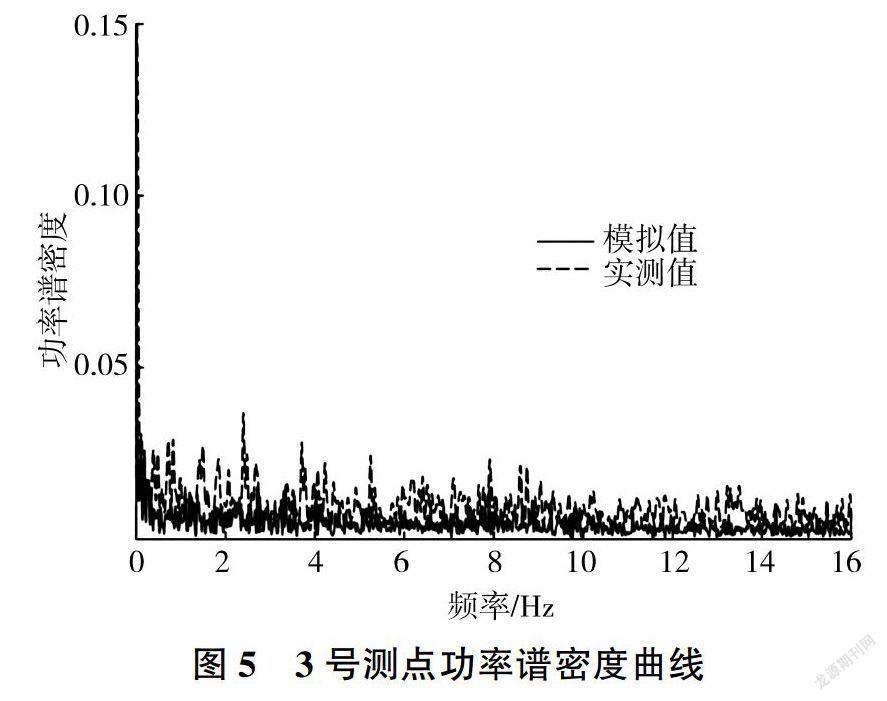
脉动压力在频域的分布用功率谱密度函数表示，它反映了脉动压力的功率在频域内随频率的分布。图4、图5为2、3号测点脉动压力功率谱密度曲线图。可以看出，模拟值与实测值的功率谱密度相似程度较高，模拟值稍小于实测值。同时，虽然各测点位置不同，但功率谱均表现为低频窄带分布，不同测点优势频率非常接近，脉动频率主要集中在0～1Hz。这是由于在此工况下，水垫塘内水位较低，水垫塘底板承受的冲击力较大，低频大尺度旋涡对脉动压力作用最主要，因此低频脉动占有很大的优势。

4 结论

基于FLOW-3D软件，选取RNGk-ζ紊流模型和VOF法追踪自由水面对某高拱坝水垫塘底板脉动压力进行了数值模拟，计算得到的动水压力时均值、脉动压强系数、概率密度分布和功率谱密度与物理模型试验结果吻合较好，相对误差较小，表明采用数值模拟方法模拟水垫塘底板压力的脉动是可行的，结果是可信的。