基于激光传感器的移动机器人地图创建研究

，

(西安工程大学 电子信息学院，西安 710048)

引 言

激光测距仪相对于其他传感器在环境感知上具有较高的数据采样频率、采样精度、采样角度分辨率等[1]。近几年来，对于激光测距仪环境感知的研究进展迅速。Cristiano Premebida 将环境用直线段、圆和椭圆的集合来表示，并介绍了在激光数据中提取上述特征的方法，并通过实验比较各算法的异同[2]。

Xavier J提出了一种基于内接角的特征提取算法，提取出环境中的直线段、圆弧和人腿的轮廓等特征[3]。Zhang S利用扩展卡尔曼滤波算法对环境进行实时直线段和圆弧特征提取，提高了特征提取的效率[4]。L Iocchi利用Hough变换的方法进行特征提取，但是该方法效率比较低，尤其是在提取圆特征时，参数空间维数升到三维，特征提取的效率将会更低[5]。Weiss G和THOMAS R通过建立激光数据点集的特征直方图提取环境中的不变特征，这种特征提取方法不同于上述几种方法，是将特征抽象为环境中的不变因素的结果[6-7]。K LINGEMAN利用一维线性滤波器对激光数据点集进行滤波，然后选取极值点作为特征点[8]。

本论文主要是研究地图中的局部地图创建[9]，在未知环境中，如何通过传感器提取出环境和障碍物信息，是创建地图的关键。在未知环境下地图的表示方法有栅格[10]、几何[11]、拓扑[12]。参考文献[13]提出对激光测距仪用加权最小二乘拟合方法提取二维水平环境特征、对单目视觉使用非局部最大抑制算法提取垂直物体边缘的方法进行信息融合。

1 环境地图表示

环境模型的建立通常是通过建立环境地图来实现。地图是移动机器人内部对外部的认识，是机器人运动的基础。目前，移动机器人常用的地图表示方法有三种：栅格地图(grid-based map)、几何特征地图(geometric feature map)、拓扑地图 (topological map),环境地图表示如图 1 所示。

图1 环境地图的表示

基于栅格的地图表示方法将整个环境分为若干相同大小的栅格，对于每个栅格指出其中是否存在障碍物，图1(a)为一幅典型的栅格地图,这种地图表示方法非常适合于超声阵列、激光测距仪等范围传感器的地图创建过程。

基于几何特征的地图表示方法是指机器人从收集的环境感知信息中提取更为抽象的几何特征，这些几何特征也称为路(Landmark)，应用这些特征对环境进行描述,图1(b)为一幅典型的点特征地图。

拓扑地图也是一种紧凑的地图表示方法，这种方法将环境表示为一张拓扑(Graph)，图1(c)显示了某一室内环境的拓扑地图，地图中的节点由室内墙壁的拐角及机器人可达的局部区域等组成，拓扑图的连接弧表示节点间的连通关系。

对于一个具体的机器人地图创建问题要根据实际环境、任务以及传感器特性选择合适的地图表示方法。上述地图表示方法并没有严格的界限，实际应用中很多系统都是综合应用这些表示方法。

2 局部地图创建

通过坐标变换可以得到数据点的全局坐标，下一步将激光传感器采集到的离散数据信息处理成用来表示环境信息的连续特征信息。采用“聚合-分割-聚合”的方法，最后得出线段的参数以及线段特征表示的局部环境地图。

2.1 机器人坐标系转换

激光测距传感器是在扫描平面上按一定的角度分辨率进行距离扫描，扫描数根据极坐标形式给出，则其直角坐标表示为：

Un=(xn,yn)T,n=1,2,…,N

(1)

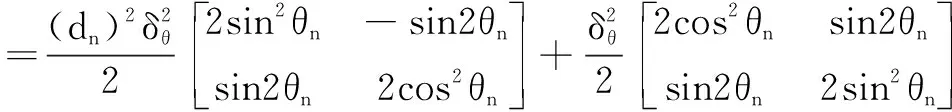
(2)

机器人坐标系与全局坐标系的关系图如图2所示，为了计算方便，假设传感器坐标系和机器人坐标系重合，在传感器坐标下得到的激光传感器扫描数据应该转换到全局坐标系中。

图2 机器人坐标系与全局坐标系的关系图

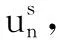
(3)

其中：

(4)

2.2 区域分割

通过坐标变换，把通过激光传感器测量得到的361个数据点的信息转化为全局坐标下的笛卡尔坐标。将361个离散数据点按照连续两点间的距离大小分成彼此不连续的区域，首先假设这361个数据点为一个区域，起点为第一个点，终点为361个点，可得到这样一个区域:

A1=((X0,Y0),(X1,Y1),…,(X360,Y360))

区域分割的具体步骤如下：

① 按照式(5)计算连续两个点之间的距离

(5)

其中j=1,2,…,360;i=1,2,…,360。

② 判断Dj和阈值δ的关系(δ的选取主要依据经验)，如果Dj大于阈值δ，则认为点(Xj,Yj)是两个区域分割点，以该点为分割点将区域分为两部分，可以得到区域A1((X0,Y0),(X1,Y1),(X2,Y2),…,(Xj,Yj))、A2((Xj+1,Yj+1),(Xj+2,Yj+2),…,(X360,Y360))。按照同样的原则对区域A2((Xj+1,Yj+1),(Xj+2,Yj+2),…,(X360,Y360))进行分割，得到A2。以此类推，最终得到相互不连通的区域(A1,A2,…,AN)。

③ 判断每个区域内的数据点个数，若包含≤3个数据点，则视该区域为噪声区域，舍弃这些噪声点。

2.3 IEPF改进线段提取

经过区域分割，得到了可以用线段描述的区域Ai(i=1,2,…,N),这些区域可能是一条或者多条线段的组合，将每一个区域分割为若干点集，其中每个点集Li可用一条线段表示L(L1,L2,…,Lm)。

由于各区域距离激光测距仪的距离不同，包含数据点的个数也不同，为了提高精度，采用动态阈值的办法。

2.4 线段拟合

经过上面的处理，可以得到存在线性关系的一组点Li(i=1,2,…,M)，但由于这些数据在测量过程中存在噪声，并不是严格线性关系，所以需要寻找一条能最大程度反映这些点关系的线段。本文采用最小二乘直线拟合方法，使全部测量点都在这条直线上：

ρcos θcos α+ρsin θsin α-r=ρcos(θ-α)-r=0

(6)

式中：r为坐标原点与这条直线的垂直距离，α为距离直线与 x 轴的夹角。由于存在测量误差，所以上式不为零。对于特定的点(ρi，θi)，它与直线之间的正交距离di为：

ρicos(θi-α)-r=di

(7)

考虑到各测量有相同的不确定性，对于全部的测量点可以将所有的误差的平方和加在一起，将直线和全部测量之间的整个拟合进行量化，如下所示：

(8)

由于直线可以由 r 和α 确定，所以可以选择直线参数(α, r)使 S 最小。要达到这个目的，通过求解非线性方程组即可得到：

(9)

(10)

由式(8)和式(10)解得：

(11)

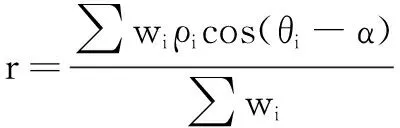
经过最小二乘线段拟合算法,得到了这条线段的最优解。

3 全局地图创建

完成局部创建后，将下一个局部地图与当前地图进行数据匹配，即比较更新后的局部地图和当前全局地图的线段关系，把局部地图的数据融合到当前全局地图中，完成地图更新，得到全局地图。

地图更新的关键问题在于解决全局地图与局部地图中的线段相关性[14]。局部线段与全局线段如图3所示，实线代表全局地图中的线段，虚线为局部地图中的线段。分为4种情况，L1、L2 与L分别重合、部分重合。L3与L1相交，L4不在全局地图中。

图3 局部线段与全局线段

具体算法如下：

① 根据线段的判定方法可以将局部地图中的线段分为与全局地图相关的线段和全局地图不相关的线段。

② 如果局部地图中的线段与全局地图的线段是同一条线段，就直接把局部地图中的线段删去，保留全局地图的线段。

③ 如果局部地图中的线段是全局地图的线段的一部分，就直接把局部地图中的线段删去，保留全局地图的线段。

④ 局部地图中的线段与全局地图相关线段是部分重合的，需要重新计算线段的参数，取出局部地图和全局地图相关线段的原始数据信息，得到一条新的线段加入到全局地图中，同时删除全局地图和局部地图中原来的线段。

⑤ 如果局部地图中的线段和全局地图中的线段不相关，则可以直接把局部地图的线段插入到全局地图中，同时从局部地图中将该线段删除。重复以上步骤，直至局部地图中的线段为空，这样就完成了局部地图到全局地图的融合，更新了全局地图。

4 实验结果

激光传感器采集0～180°范围数据，角分辨率为0.5°，实验环境为学校实验室。实验过程中先区域分割，然后特征提取，最后拟合成直线，生成局部地图，再通过局部地图的融合，得到全局地图。生成的局部地图与全局地图如图4和图5所示。

图4 局部地图构建

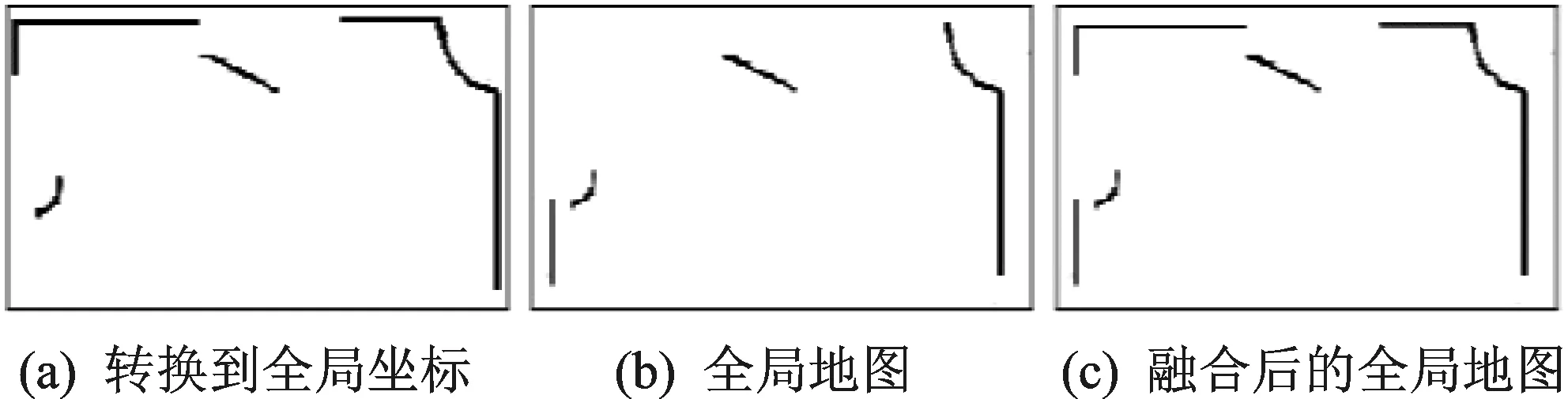
图5 全局地图构建

结 语

柯莉红、要鹏超(硕士)，主要研究方向为机器人技术。