面向单片机及嵌入式系统的AES算法改进研究
2018-09-07,,
,,
(1.湖北师范大学 计算机科学与技术学院,黄石 435002;2.湖北师范大学 物理与电子科学学院)
引 言
AES算法能够取代DES作为新的数据加密标准,原因就在于 AES不仅全面继承了DES的优点,还弥补了DES存在的不足。AES比DES更安全,它能够抵抗目前已知的大部分攻击;AES算法在大多的平台上都可以实现,且代码比较紧凑,运行速度也很快。然而AES算法还是有着自身的不足,诸如S盒的结构需进一步优化,加、解密结构不对称,扩展密钥安全性不够等。针对AES算法的这些不足,本文提出了一些改进措施,然后通过系统仿真软件在一个最小单片机系统上对改进前和改进后的AES算法进行了比较研究。
1 AES算法简介
AES算法[1]中最重要的部分之一就是轮函数,轮函数一共包括4种计算部件,分别是字节代换(ByteSub)、行移位(ShiftRow)、列混合(MixColumn)、密钥加(AddRoundKey)。这4种部件可以看成是轮函数的3个层,即线性混合层、非线性层、密钥加层。每个层都有各自独立的功能。线性混合层是为了保证多次轮变换的高度扩散;非线性层是将具有最优的“最坏情况非线性特性”的S盒并行使用;密钥加层是对中间状态实施的一次性掩盖。
1.1 字节代换
字节代换的过程分两步进行:第一步,将字节用多项式的形式来表示,然后映射到自己的乘法逆元;第二步,映射完之后,再对字节做出仿射变换。
逆字节代换的过程[2]也是分两步进行的:先进行上述仿射变换的逆变换;再求每一个字节在有限域GF(28)上的逆元。
1.2 行移位
行移位就是对状态中的各行进行循环左移,这是一种线性运算[3]。State矩阵有4行Nb列,现设置从第0行到第3行循环左移的字节数分别为C0、C1、C2、C3,其中C0是恒等于0的。C1、C2、C3与Nb的关系如表1所列。

表1 位移量与列数的函数
逆行移位就是对状态矩阵的后3列分别以Nb-C1、Nb-C2、Nb-C3个字节数来进行循环移位。
1.3 列混合
在列混合变换中,需要将状态矩阵中的每一列视为一个向量[4],把它看成是系数在有限域GF(28)上的多项式,然后再和多项式c(x)进行模M(x)相乘。c(x)和M(x)的表达式如下:
c(x)=03x3+01x2+01x+02
M(x)=x4+1
列混合变换可以用矩阵乘法来表示,即

逆列混合变换的运算是相似的,现直接用矩阵乘法来表示如下:

1.4 密钥加
密钥加的运算[5]就是将轮密钥与状态阵列对应位的字节进行位异或。轮密钥阵列则是通过种子密钥经密钥编排算法得到的,密钥加运算的逆过程就是其自身。
2 AES算法的改进
AES算法的S盒可以说是唯一的非线性部件,因此,S盒的好坏[6]将直接影响算法的性能。根据研究可知,S盒满足平衡性,非线性度为112,严格雪崩准则距离为432,差分均匀度为4,仿射变换对周期为4。总的来说,S盒的性质[2]还是不错的。不过,S盒的仿射变换对周期最大可以取到16,其次是8,标准算法选用的是周期为4的仿射变换对;迭代输出周期不大于88,代数表达式仅有9项,存在周期过小、项数过短的不足。此外,AES算法中加密解密轮变换顺序不一致给算法的实现带来了不便;扩展密钥中存在着前后轮密钥关联性过强、易推导的缺陷。现从以下3个方面对算法做出改进。
2.1 S盒上的改进
AES算法的S盒之所以存在上述不足,主要与选用的仿射变换对和S盒构造方式有关。所以,现提出一种新S盒的构造,新S盒的构造分如下3步进行:
① 选用仿射变换对(‘6B’,‘5D’)进行仿射变换:
② 进行乘法求逆。
③ 再进行一次步骤①的仿射变换。
逆S盒的构造方式与S盒是一样的,(‘6B’,‘5D’)的逆仿射变换对为(‘70’,‘4A’),逆仿射变换定义为:
2.1.1 新S盒代换表
有限域GF(28)中一共只有256个元素,如果把这256个元素全部进行一遍改进后的字节代换,对应的结果绘制成表格,就可以得到新S盒代换表。
2.1.2 新旧S盒对比
旧S盒与改进后的新S盒密码性质对比如表2所列。

表2 新旧S盒性能对比
比较结果表明,改进后的新S盒既保留了原S盒的优点,又弥补了原S盒在仿射变换周期、迭代输出周期、表达式项数过短上的缺点。
2.2 结构上的改进
2.2.1 加密结构上的改进
在分组长度为128位的AES算法中,迭代轮数Nr为10。前9轮的轮变换顺序都是一样的,依次进行字节代换BS、行移位SR、列混合MC、密钥加AK。现将前9轮变换中行移位和列混合操作进行合并,设某轮字节代换后的状态为S1,该轮密钥加之前的状态为S2,则:
如果将矩阵S1和S2看成是一维数组的话,那么上述的运算经过变形就可以改为:
2.2.2 解密结构上的改进
在AES加解密算法中,轮函数的4个部件计算顺序并不相同,这导致加解密对应着不同的模块,给算法的实现带来了不便。加解密过程中轮变换的顺序如图1所示。
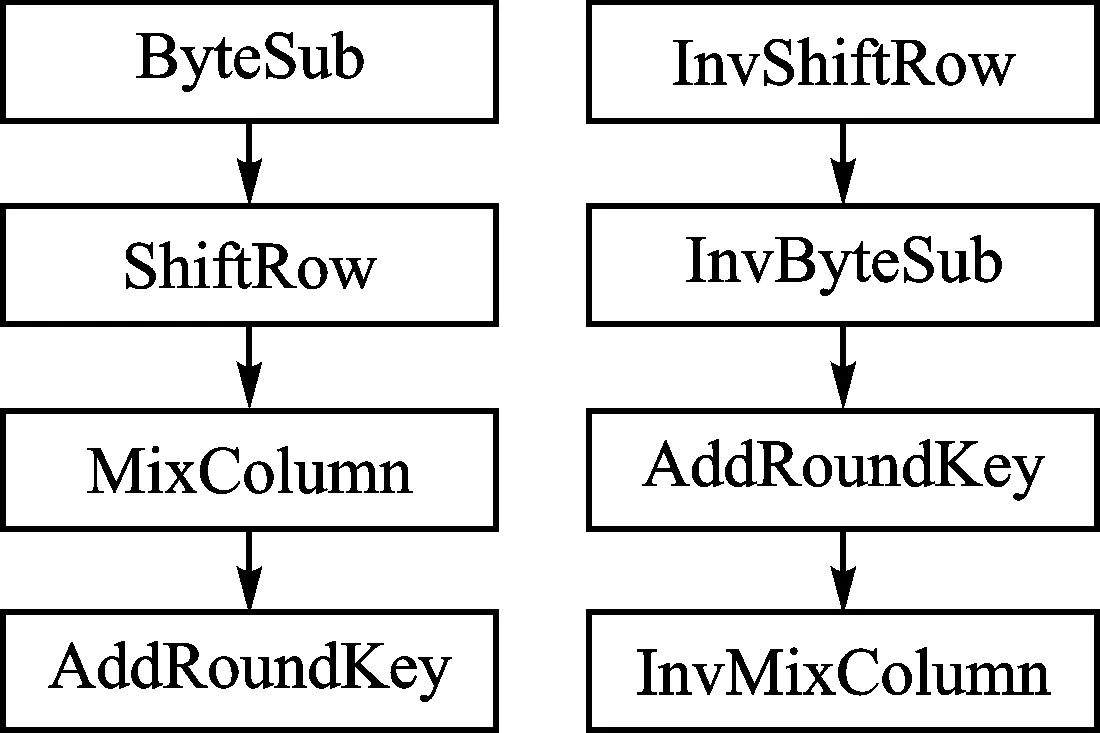
图1 AES加解密过程轮变换顺序
针对这一问题,可以调整解密轮变换的顺序,使得加解密轮变换顺序保持一致。InvShiftRow和InvByteSub的交换比较容易理解,现给出AddRoundKey和InvMixColumn可以交换的证明,设状态矩阵为X,该轮的轮密钥为W,如下:
调整解密算法的轮变换顺序后,也可以合并逆行移位和逆列混合操作,现直接给出结果(见下页):
2.3 密钥扩展上的改进
在原密钥扩展算法中,最初的Nk个字就是种子密钥,之后的每Nk个字都是由前Nk个字递归得到。由扩展密钥的生成过程可以得出,虽然每一轮密钥的生成都经过了复杂的变换,但该轮密钥与上一轮密钥间有着密切的关联。如果截获了某一轮密钥,逆推出上一轮密钥只需要穷举232次。因此,现在提出一种新的密钥扩展方式。
2.3.1 新密钥扩展方式
新密钥扩展方式原理如图2所示。
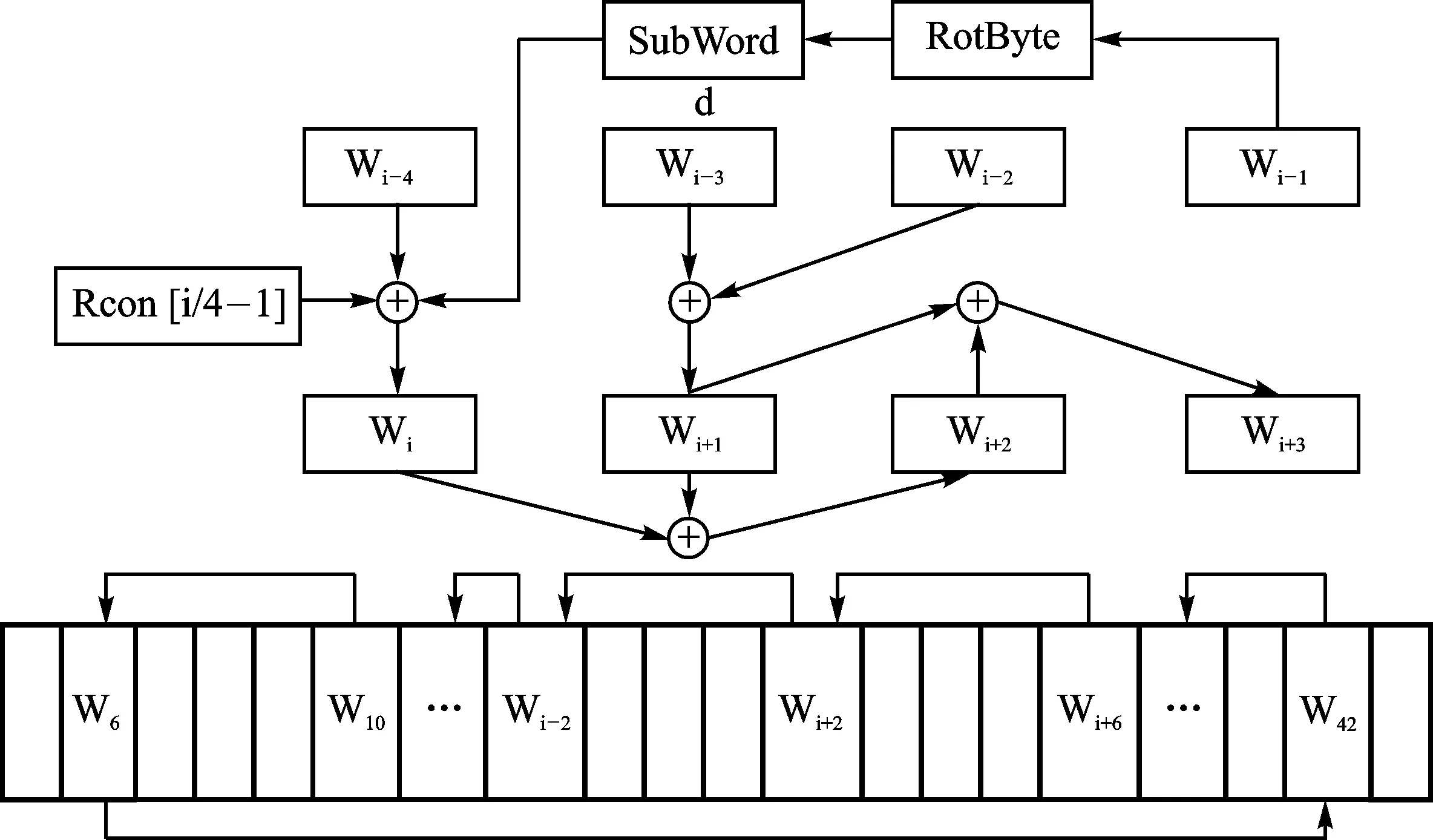
图2 新密钥扩展方式原理图
在原密钥扩展算法中,Wi+1、Wi+2、Wi+3都是采用同一种方式生成,而这正是它脆弱的地方。现保持原算法中其他过程不变,仅改变Wi+1、Wi+2、Wi+3的生成方式。Wi+1由Wi-3和Wi-2异或得到,Wi+2又由生成的Wi+1与Wi异或得到,Wi+3就由Wi+1和Wi+2异或得到。最后,再补加一个Wi+2的外轮循环移位。
2.3.2 新旧密钥扩展算法对比
将原密钥扩展算法和改进后的算法在Keil环境下用单片机C语言来实现,单片机的型号为AT89C55,CPU的频率为12 MHz,模拟得出算法的性能对比,对比结果如表3所列。

表3 密钥扩展算法改进前后对比
3 仿 真
Proteus是一款常见的系统仿真软件,现将原AES标准算法和改进算法用Proteus进行仿真,测试改进前后算法的性能。T1和T2分别表示改进前后算法中密钥扩展函数运行所花费的时间(ms),S1和S2分别表示改进前后算法在单片机中所占据的空间大小(KB)。改进前后算法的仿真运行分别如图3和图4所示。

图3 改进前AES算法的仿真
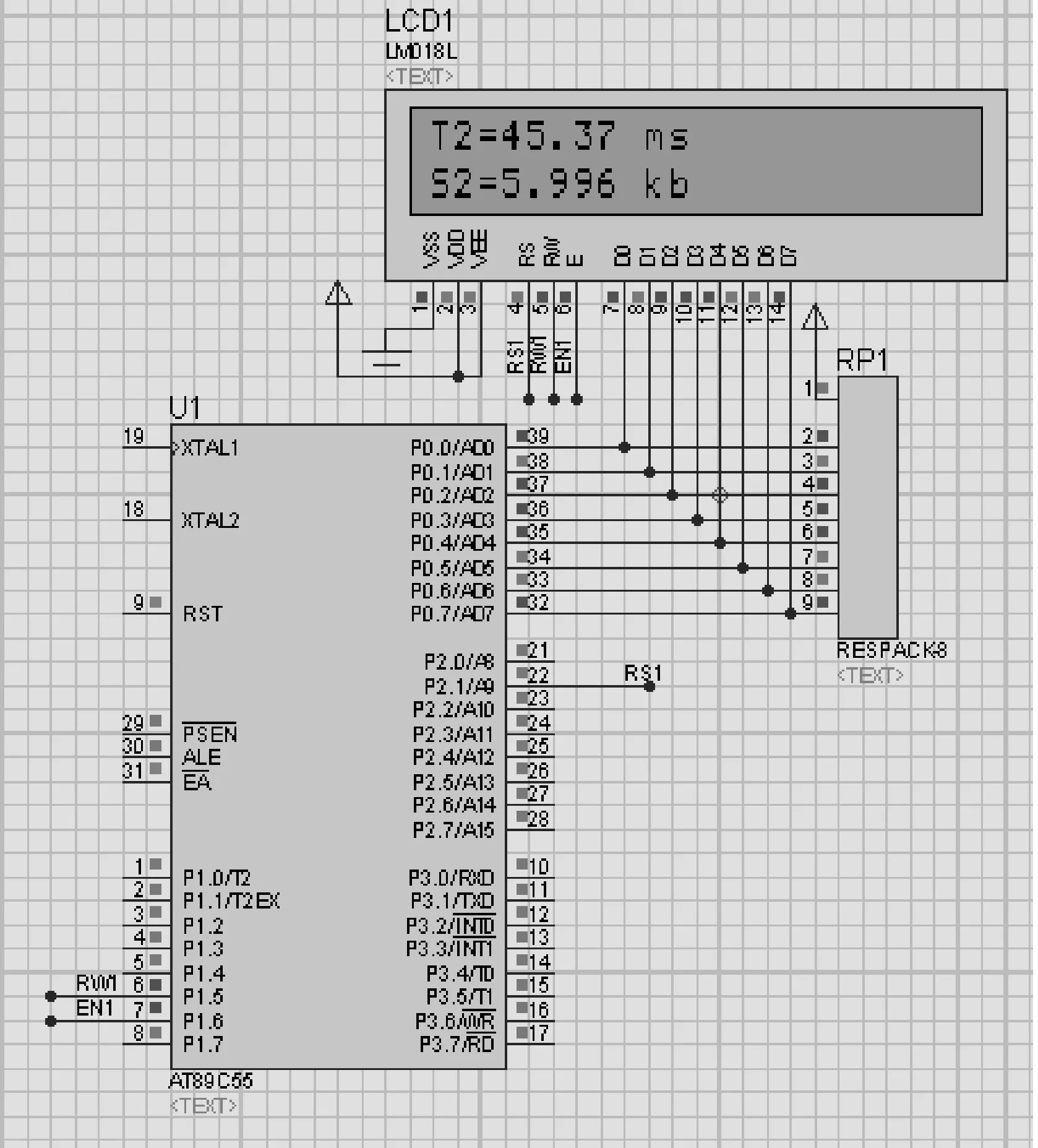
图4 改进后AES算法的仿真
通过在相同的硬件和软件环境下仿真运行,标准AES算法运行所占据的空间大小为6.025 KB,其中密钥扩展函数代码执行所花费的时间为45.46 ms,而改进后算法运行所占据的空间大小为5.996 KB,密钥扩展函数代码执行所花费的时间为45.37 ms。
结 语

周炳(硕士研究生),主要研究方向为信息与智能计算。通信作者:洪家平(教授),硕士生导师。
