基于多相流的轴流血泵流场分析及溶血指数预测

王带领，谭建平，喻哲钦



基于多相流的轴流血泵流场分析及溶血指数预测

王带领，谭建平，喻哲钦

(中南大学 机电工程学院，湖南 长沙，410083)

为研究血泵内部血细胞分布规律及溶血预测方法，以自制轴流血泵为例，应用多相流分析方法，采用多重参考坐标系法(MRF)等技术建立数值分析模型，并通过体外循环实验验证模型的有效性。进一步分析血泵内部血细胞浓度、速度、压力等的分布规律，得到血细胞破坏区域和一般规律。根据优化的溶血模型对血泵的溶血性能进行评估，在此基础上提出溶血实验指标标准溶血指标(NIH)与溶血预测值之间的转换关系。研究结果表明：血细胞在血泵内部不是均匀分布，叶轮处有明显分离现象；血泵内部剪切应力在 200 Pa 以下的区域的体积分数约为98.6%，高剪切应力主要位于叶轮顶部和外壳的间隙处；在剪切应力为常数时，优化的溶血预测模型和Giersiepen实验得到的溶血模型相符合；采用优化模型计算得到血泵平均溶血预测值0.005 7，具有较好的溶血性能。

血泵；多相流；标准溶血指标；溶血模型

血泵已经成为帮助心脏功能障碍患者的一种有效方法。血泵经历了从容积式到悬浮技术的变革，其在驱动控制、生物相容性、等方面都有了极大的发展[1]。在血泵的设计开发中，计算流体力学(CFD)得到了普遍应用。基于血泵虚拟样机的血液动力学性能数值分析能够极大地缩短设计周期，节约成本[2−3]，但同时伴随着一些问题，其中溶血和血栓尤为突出[4−5]：因此，研究数值模拟血泵内部流场特性和溶血预测算法对优化血泵设计具有重要意义，国内外学者为寻找一种有效的溶血预测方法进行了广泛研究[6]。YANO等[7]采用拉格朗日粒子追踪法对血泵的溶血性能进行了数值分析，并与实验结果进行对比，验证了模型的合理性。GARON等[8]通过欧拉法建立了快速溶血模型，通过体外溶血实验对模型进行了验证。TASKIN等[9]通过设计特定的溶血实验设备，比较了拉格朗日几种幂律模型和欧拉模型的区别，实验结果表明欧拉模型溶血预测误差较大。LI等[5]使用多相流模型对轴流泵流场进行了仿真分析，并提出了基于剪切应力的溶血估计算法，通过实验进行验证。周冰晶等[10−11]通过拉格朗日粒子追踪法对自主研发的血泵进行了溶血预测，从而对血泵结构优化提供了理论指导。寿宸等[12]通过比较4种不同叶轮形式的离心血泵仿真结果，并采用快速溶血模型进行溶血预测，发现螺旋线叶轮性能较优。以往的CFD分析中大都把血液近似为单一牛顿流体进行数值计算。采用单一流体一方面不能得到血细胞在血泵内部的分布规律；另一方面，简化的血液模型与实际结果有差异，不能反映血细胞对流场的影响，难以揭示真实血液的流动规律。鉴于血液组成的复杂性，本文作者通过采用多相流模型，兼顾血细胞与血浆的相互作用，使模拟流动与实际流动更接近，分析血细胞体积浓度、速度，压力等的分布规律。并在原有的拉格朗日粒子追踪法的基础上，考虑加载历史对溶血的影响，提出优化溶血模型，并对两者进行比较分析。人们普遍采用标准溶血指标(NIH)对血泵的溶血特性进行评估[5]，考虑到NIH与溶血预测值这2个指标的意义和计算方法的区别，提出标准溶血指标(NIH)与溶血预测值之间的转换关系。

1 模型及算法

1.1 血泵模型及网格划分

课题组自主设计了一个由磁力驱动的微型轴流血泵，包含前导、叶轮、后导、永磁体，轴承等结构。前导叶和后导叶有导流作用，叶轮采用螺旋结构，其高速旋转促使血液运动并获得压能，从而起到辅助人体心脏泵血的功能；永磁体放置在叶轮部分，分为N和S两极，通过与由单片机控制的三齿槽定子驱动线圈的相互作用使血泵的叶轮持续转动[13]。血泵进出口直径为16.4 mm，叶轮轮缘直径为16.0 mm；模型总长81.0 mm。图1所示为血泵结构示意图。

将血泵几何文件导入到ICEM中划分网格。由于流体域各部分运动状况不同，把模型划分为3部分即前导叶区，叶轮区，后导叶区，使用多重参考坐标系法(MRF)，分别建立动静坐标系，并在动静区域创建交界面。因为叶轮、导叶结构较复杂，使用非结构化网格技术进行处理，共得到2 410 710个网格单元。图2所示为网格划分示意图。

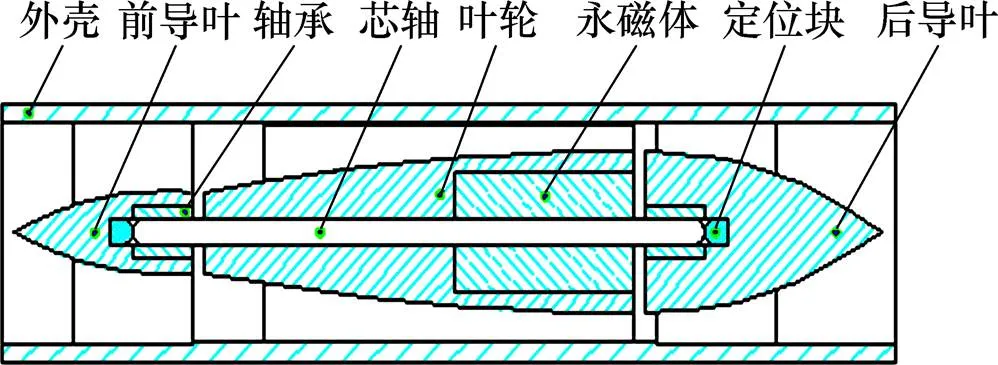
图1 血泵结构示意图

图2 网格划分示意图

1.2 欧拉多相流模型

红细胞是血液的重要构成成分，约占血液体积的40%。由于血液成分复杂，因此，选用多相流进行模拟。在多相流模型中，欧拉模型能较好地模拟固相体积分数超过10%的情况，且与其他模型相比具有较高的求解精度，因此，选用欧拉模型进行仿真计算。

将血浆定义为液相，其密度为1.03 t/m3，黏度为1.60 mPa∙s；红细胞定义为固相，其密度为1.09 t/m3，黏度为6 mPa∙s[14]。人体中成熟的红细胞为双凹面圆盘状，直径为7~9 μm，为了简化模型，固相(红细胞)假设为球形，直径均匀，计算中取值为8 μm。

1.3 边界条件及算法

为了满足人体基本的生理需求，血泵设计要求进出口压差约为13.3 kPa，流量为5 L/min。入口使用速度进口边界，根据流量和截面积，计算出进口速度为0.4 m/s。出口使用压力出口条件，压力为13.3 kPa。血泵叶轮区域的壁面设置为旋转边界，其转速与叶轮区的转速相同，该血泵设计工况为8 000 r/min。其余壁面定义为无滑移固壁边界。进口红细胞体积分数设置为40%。

模型采用标准的−湍流模型，使用simple算法，离散格式设置为二阶迎风。

1.4 仿真模型验证

为验证仿真模型的可靠性，搭建血泵体外循环实验系统，设计工况下进行体外循环性能实验。该实验系统主要由储液槽、血泵、驱动线圈、压力传感器、涡轮流量计、电动阀及各支架和管道等组成。压力传感器分别测量血泵进出口压力，涡轮流量计测量血泵输出流量。实验中循环介质采用体积分数为37%的甘油和水的混合溶液，其在常温条件下，动力黏度和血液的匹配。设定叶轮转速为8 000 r/min，并调节血泵进出口压差为13.3 kPa。

在上述工况下进行血泵性能实验。表1所示为体外循环实验中实验流量与仿真结果之间对比。由表1可知：在8 000 r/min下血泵的平均流量约为4.8 L/min，基本满足人体生理需求；其中测量值与仿真值之间的最大误差为4.2%，均小于5.0%，误差在允许范围内。实验结果在一定程度上验证了血泵数值仿真模型的有效性，为后续血泵流场分布规律的研究提供了保证。

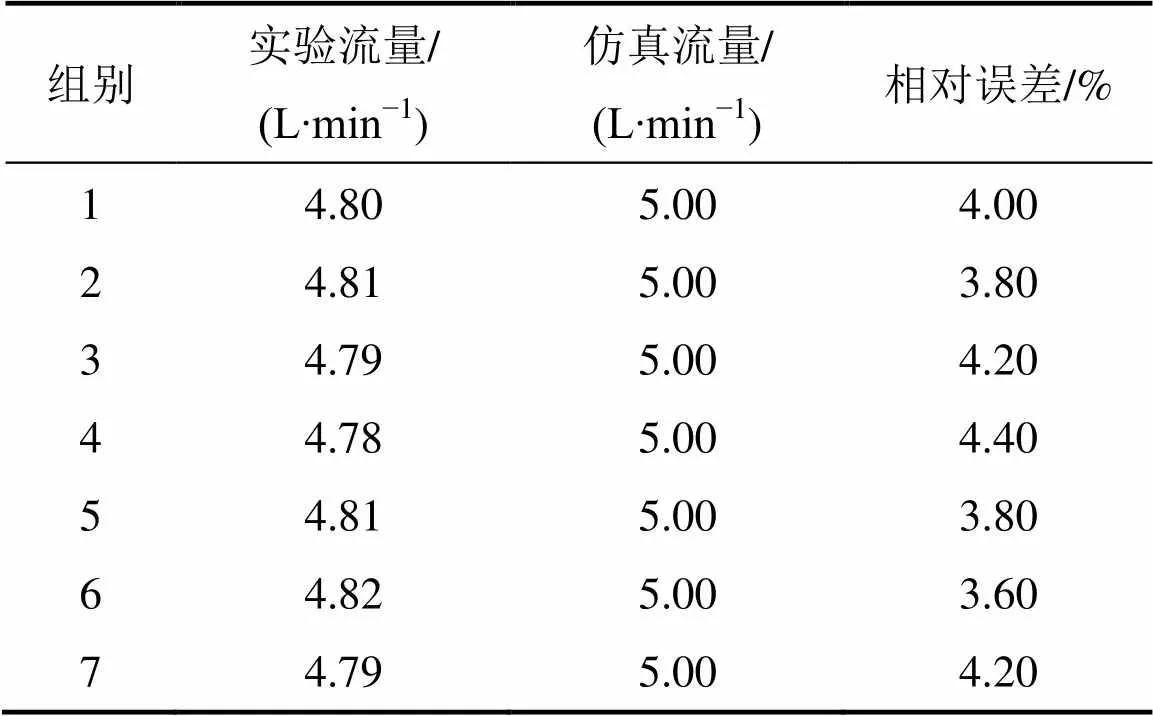
表1 实验流量与仿真流量比较

2 仿真结果分析

2.1 固相体积分数分布

按照上述参数和算法设置，对血泵内部两相分布情况进行数值分析。图3所示为血细胞体积分布云图。从图3可见：血细胞在血泵内部并非均匀分布，体积分数为35%~42%。其中，前导叶区域由于没有运动部件，流动较平稳，血细胞体积分数分布均匀，约为40%。随着进一步流动，在叶轮区域，由于叶轮的高速旋转和因离心力与惯性的影响，血细胞的体积分数逐渐开始发生变化，其中，在叶轮前端部分差异不明显，随着轮毂增大，血细胞逐渐偏向叶轮轮缘处。特别是在叶轮分流叶片处，轮毂处附近血细胞体积分数减小，叶轮工作面及轮缘处血细胞浓度有明显增大，达到42%。当血细胞运动到后导叶区域，由于导叶的导流作用，切向速度减小，轴向速度增加，流动再次趋于平稳，血细胞浓度分布重新变得均匀。由于血细胞和血浆密度接近，并且血细胞直径较小，从而对流场的影响有限，各部分体积分数差异不是很大，仅在叶轮区域存在小程度的分离现象。

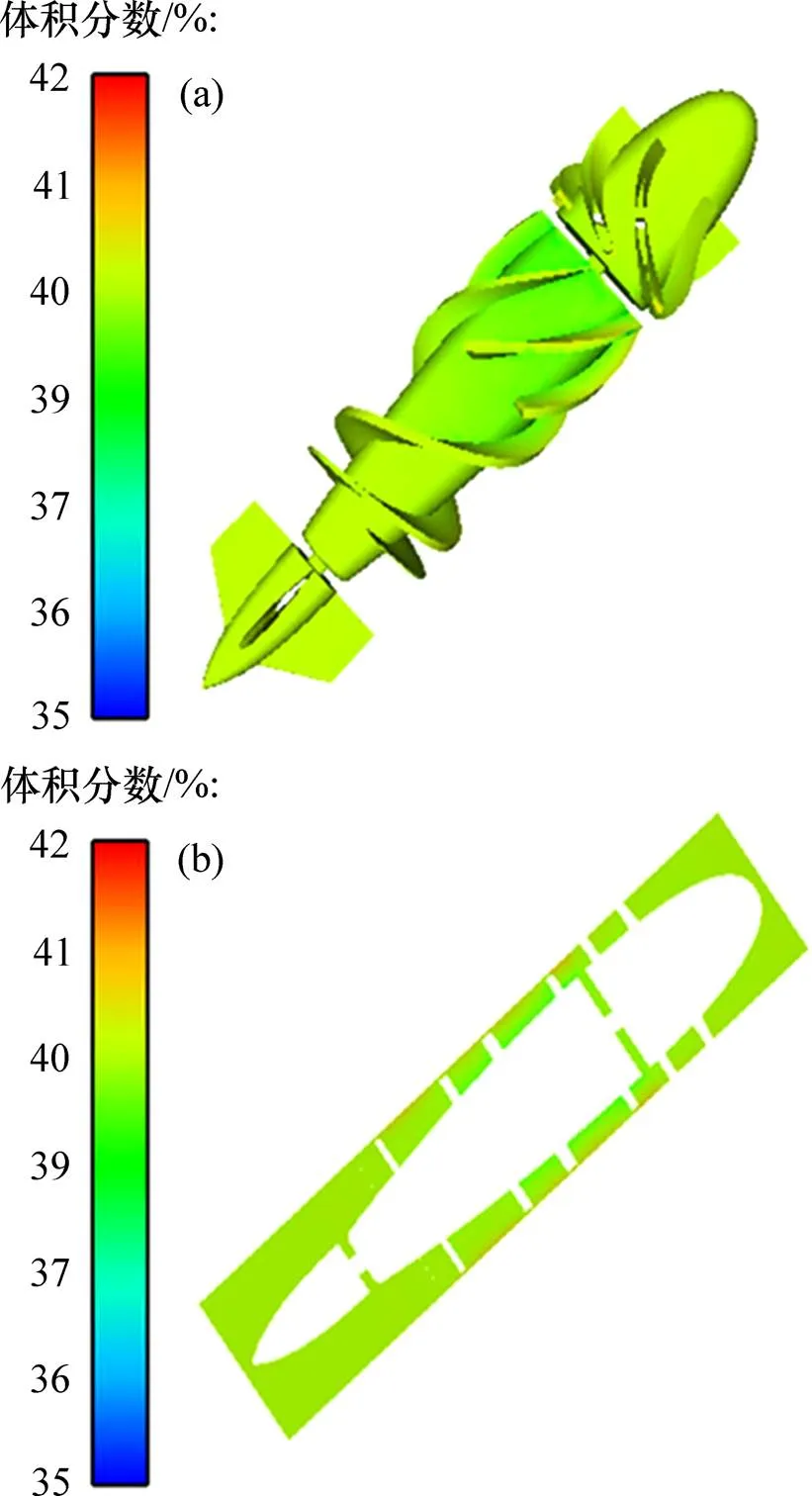
(a) 血泵内部体积分数；(b) 轴截面体积分数

2.2 速度与压力分布

图4所示为轴截面单相与两相速度分布。由图4可见：两者速度分布基本相同；在血泵进口位置，速度较小；在叶轮部分，由于轴流血泵的叶轮具有极高的转速，从轮毂沿着径向速度逐渐增大，特别是在叶轮边缘具有较大的速度梯度，对细胞破坏作用大；在出口部位，由于导叶的作用，速度较均匀。多相流下液体的最大速度略大。这是因为在叶轮边缘血细胞体积浓度较高，血细胞与血浆的相互作用，血浆速度增大。云忠等[15]发现红细胞其垂直撞击速度超过6 m/s，有发生破碎的可能。从图4可见：血液最大流速达 6.95 m/s，特别是在轮缘与外壳之间的区域，红细胞有破碎的危险。

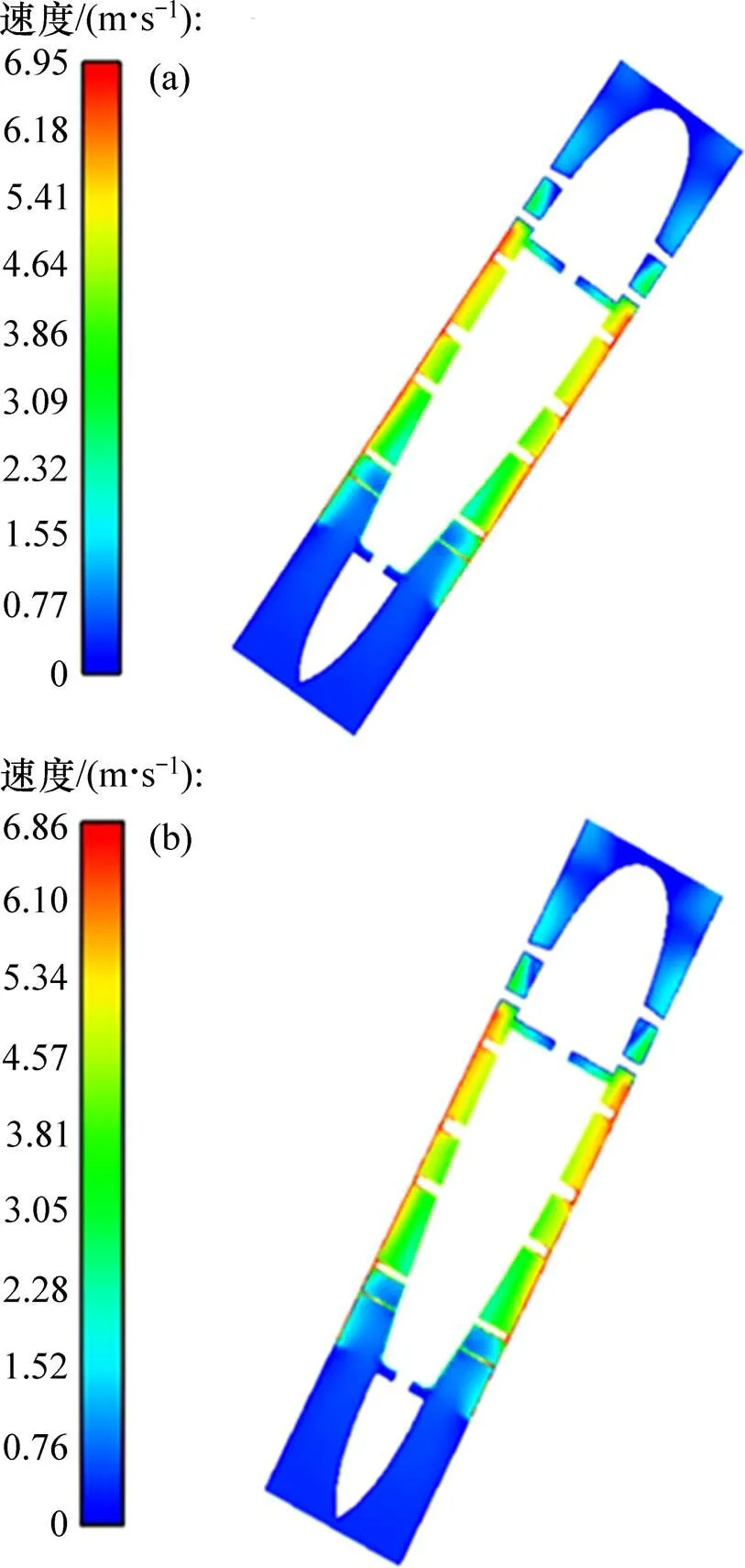
(a) 两相流速度云图；(b) 单相流速度云图

图5所示为血泵轴向截面总压分布。由图5可见：入口处压力较小；流道内沿着流动方向，压力逐渐增大；分流叶片处具有较大的压力梯度，对红细胞的损伤较严重；在出口区域，由于后导叶的作用，速度转换为压力能，压力分布均匀，进出口压差约为 13.3 kPa，能满足人体基本需求。

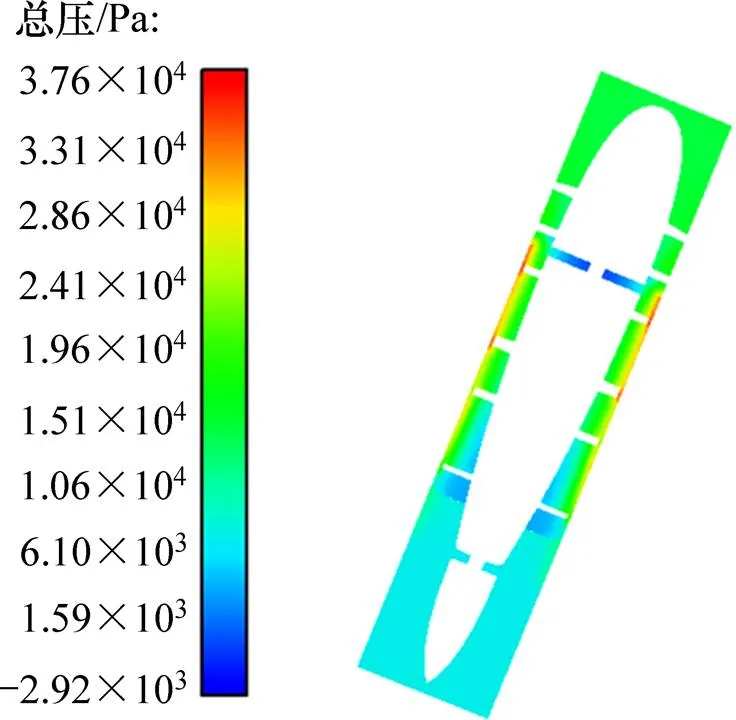
图5 轴截面总压分布云图

3 溶血预测模型

3.1 通用溶血预测模型

GIERSIEPEN等[16]通过实验得到了溶血公式。该模型指出溶血程度与流场剪切应力、红细胞在剪切应力中的暴露时间呈幂函数关系：

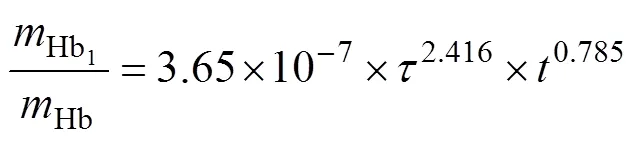
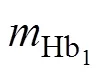
血泵内的实际流动为不规则的湍流运动，剪切应力为黏性剪切应力与湍流剪切应力的合成。黏性剪切应力与湍流剪切应力计算公式见文献[10]。剪切应力标量可以表示如下：

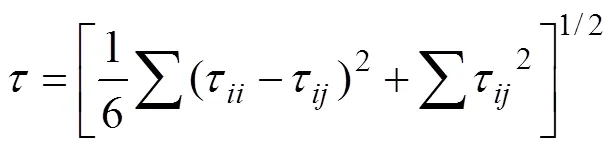
溶血算法主要有欧拉法和拉格朗日法，均基于式(1)所示的溶血实验公式进行推导。其中拉格朗日算法核心思想是：当单个红细胞流过血泵时，由于运动轨迹上各点的剪切应力是不断变化的，将粒子轨迹线分成个微小段，在任意微小时间段(=1~)内，计算溶血值，进行叠加。

YANO等[7]采用溶血算法计算任意小段时间内的溶血值：

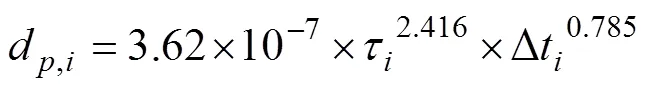
迹线上某一时刻的累计溶血值D,i可以通过D,i−1递推计算得到，递推公式如下：

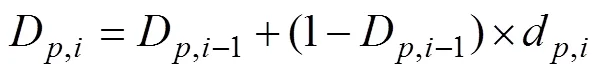
经计算，可以得到整条迹线的溶血值，对条迹线进行平均处理，可以得到血泵溶血预测值。

3.2 优化溶血模型

式(1)是基于切应力不变的情况下得出的，在剪切应力不变情况下，据式(1)，任意时间步的溶血贡献值d,i如下：

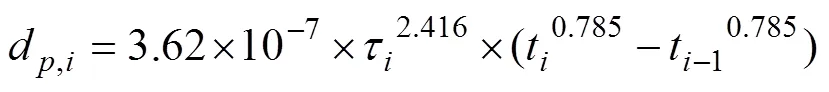
比较式(3)与(5)，YANO等[7]将每个时间步内用Δ0.785代替Δ(0.785)，因为0.785不符合线性叠加且一阶导数单调递减，即

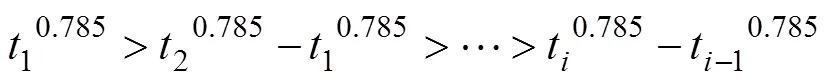
导致溶血预测值偏大。考虑到方程中时间非线性以及加载历史的影响对算法进行改进，引入等效时间。在第1个时间段d1内，若它的溶血预测值d,1为

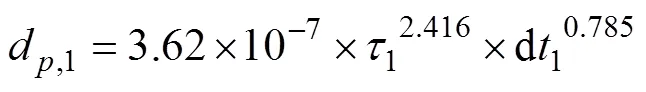
则在时间步d2，需要重新设定时间起点。为此，引入等效时间deq：

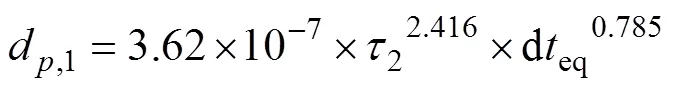
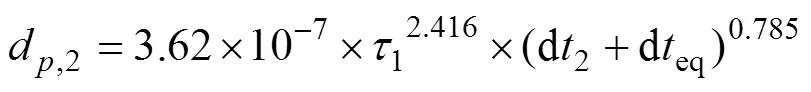
重复以上步骤，将下一个时间步重新设定的时间起点。经计算，可以得到整条迹线的溶血预测值。对条迹线进行平均处理，可以得到标准溶血预测值。假设细胞在运动过程中受到的剪切应力为常数，加载时间为0.5 s，切应力为100 Pa。图6所示为常剪切应力下不同模型的溶血预测。从图6可见：优化算法在剪切应力恒定时与GIERSIEPEN公式所得计算结果相吻合，溶血值为1.4×10−2，YANO等[7]的算法溶血值为2.0×10−2，与公式值相比偏大，分析结果一致。

3.3 溶血预测结果

标量切应力分布影响血泵的溶血性能，特别是切应力大于200 Pa的区域对红细胞有较大破坏作用[17]。图7所示为血泵内部剪切应力云图，图8所示为不同剪切应力区域在总体区域中所占的比例。从图7可见：内部最大剪切应力约为877 Pa，主要分布在叶轮和后导叶入口区域。从图8可见：剪切应力在 200 Pa 以下的区域所占比例约为98.6%，超过200 Pa的区域约为1.4%，可见使红细胞产生较大损伤的高剪切应力区域较小，这些部分主要位于外壳和叶轮顶部的间隙以及后导叶入口处，此处血细胞的浓度也较高，血细胞可能因为剪切应力较大，与叶轮剧烈碰撞而破碎。

在FLUENT中通过UDF，根据切应力标量公式定义函数。导出每条迹线上切应力与时间的对应数据文件；利用MATLAB读取数据文件并通过程序进行数据处理从而得到每条迹线的溶血预测值，进一步得到平均溶血预测值。图9所示为其中1条流线的剪切应力和溶血随时间变化规律。从图9可见：红细胞在开始阶段即前导叶区域，剪切应力较小，溶血预测值累计值基本为0；当红细胞进入叶轮区域时，速度梯度较大，剪切应力出现高峰区，溶血预测值急剧增加；当细胞经过后导叶时，流动逐渐平稳，剪切应力减小，溶血预测值基本保持不变。这2种算法所得溶血预测值变化趋势相同，YANO等[7]的算法溶血预测值较高(1.0×10−3)，优化算法溶血预测值为2.8×10−4。

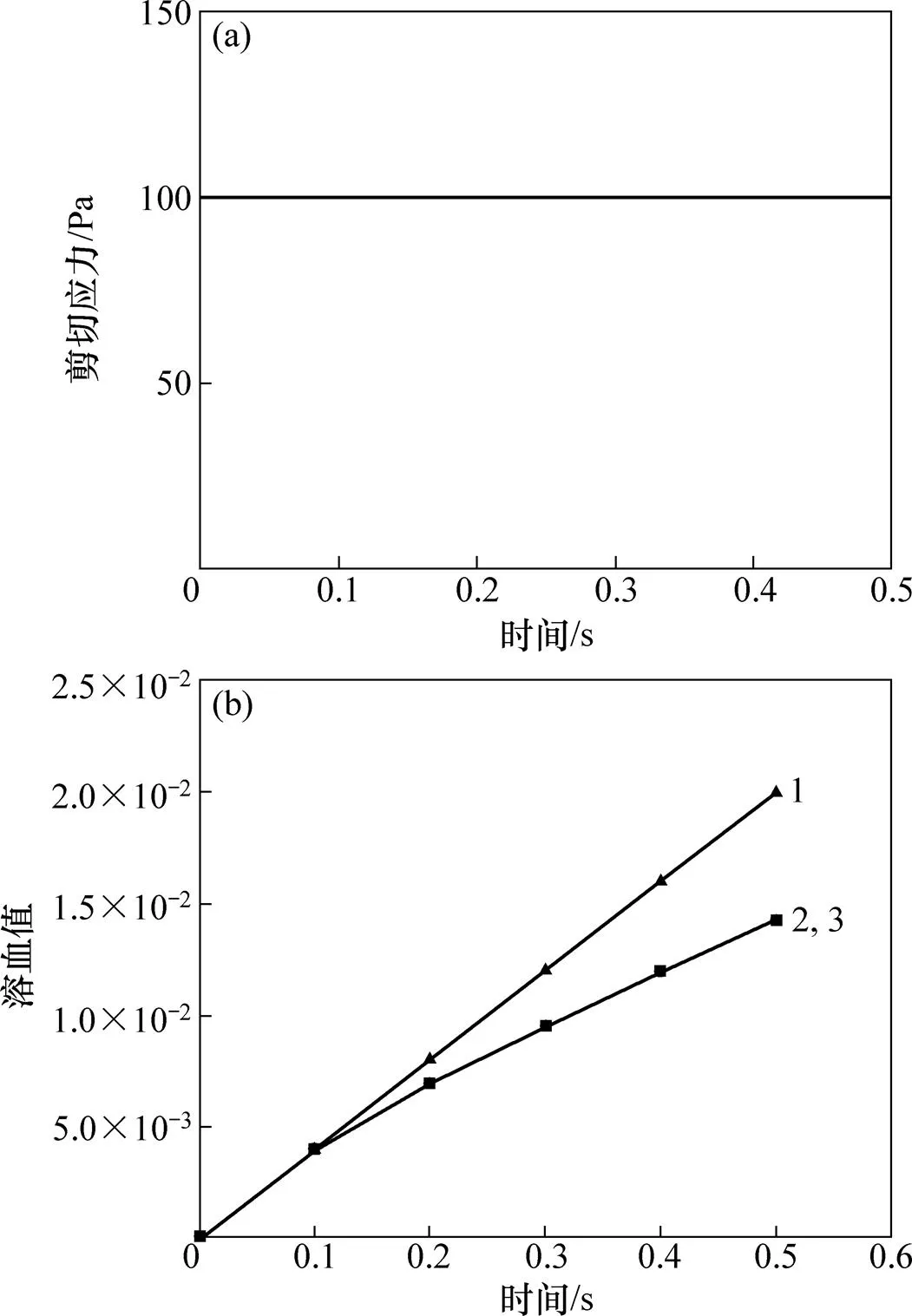
(a) 常剪切应力加载；(b) 不同算法溶血值

图7 剪切应力分布云图

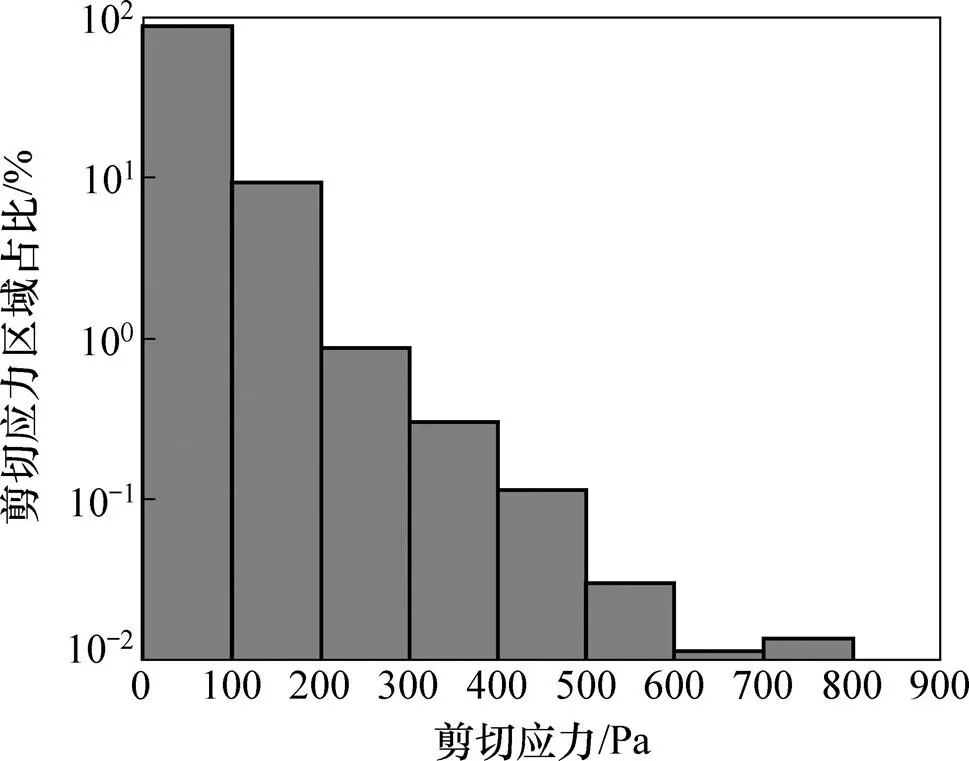
图8 不同剪切应力区域占比

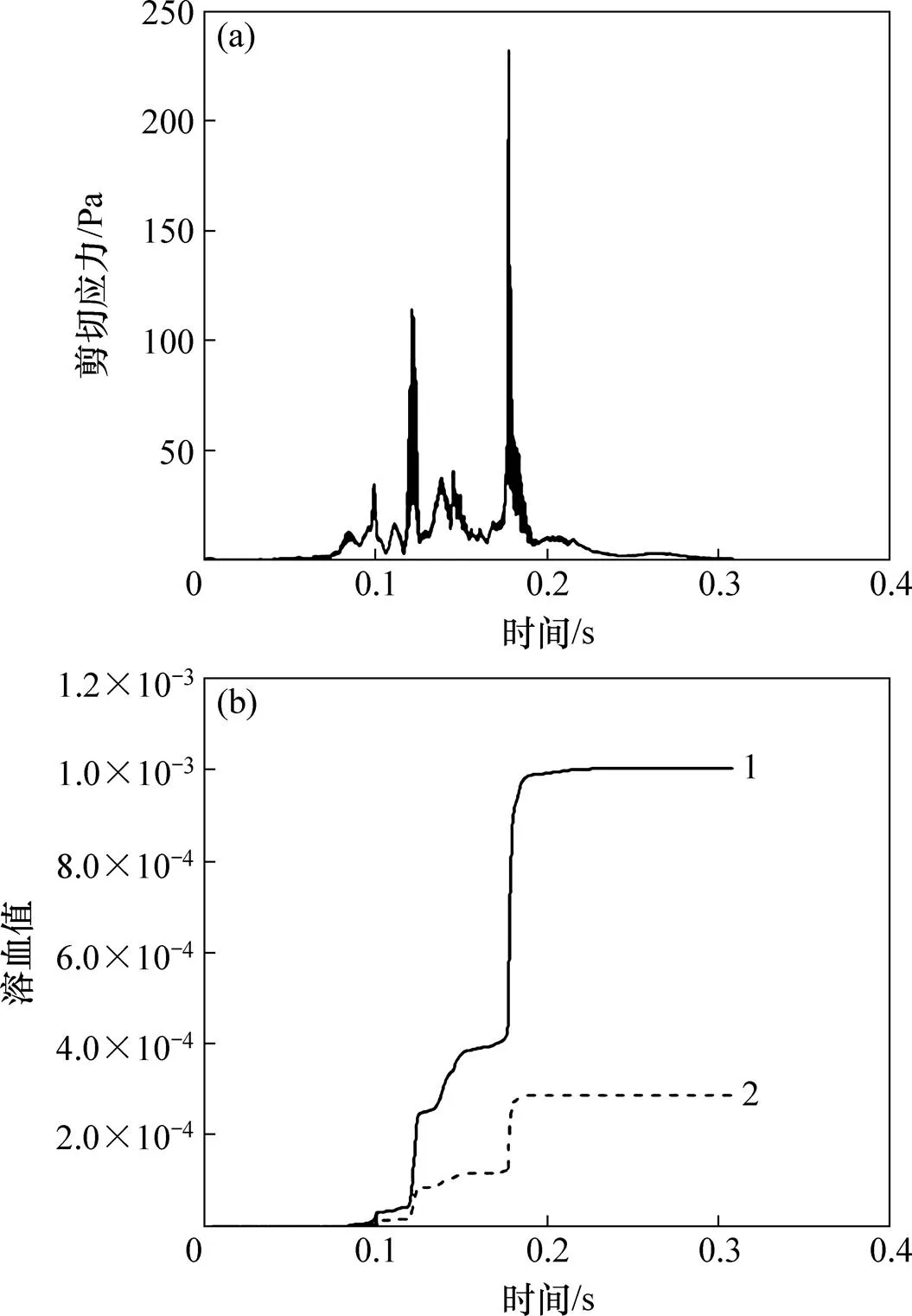
(a) 剪切应力变化；(b) 溶血变化

选取117条流线，利用优化算法对117条流线溶血值进行平均，得到血泵的平均溶血值为0.005 7，溶血性能较好，可为血泵溶血性能的数值预测提供参考。

3.4 标准溶血指标与预测值的转换

国际上，标准溶血指标(NIH)被广泛用来评估体外辅助装置对红细胞的损伤程度[5]。计算式可表示为

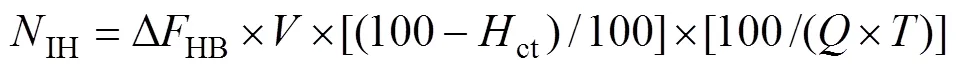
式中：ct为红细胞压积百分数，%；ΔHB为测试间隔时间内血浆游离血红蛋白的增量，g/L；为总循环体积，L；为辅助装置输出流量，L/min；为测试时间间隔，min。

溶血预测值为游离血红蛋白与血液中全部血红蛋白的比值即溶血率，为量纲一量。两者不能直接进行比较，需要通过公式建立联系来验证模型。

根据上述溶血模型单次循环溶血预测值，进行次循环的溶血估计值为D，其中0=0。D可以通过下式计算得到：

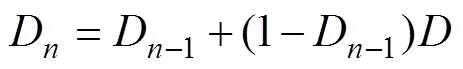
进行次循环的血红蛋白增量值ΔHB可以计算如下：

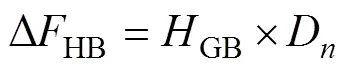
式中：GB为血红蛋白质量浓度，g/L。

通过ΔHB，利用式(10)可以计算得到标准溶血指数预测值IH，与实验结果NIH进行对比，从而评估溶血模型。

4 结论

1) 多相流模型能够揭示血泵内部血细胞分布的一般规律。血细胞在血泵内不是均匀分布的，进出口区域分布较均匀，叶轮处存在小程度分离现象。由于血细胞体积较小，且其密度与血浆的密度接近，离析现象不严重。

2) 血泵内部切应力超过200 Pa的区域约为1.4%，这些区域主要位于外壳和叶轮顶部的间隙与后导叶入口处，高剪切应力和剧烈的碰撞可能导致血细胞破碎。

3) 优化的溶血模型在剪切应力为常数时，与GIERSIEPEN的溶血实验公式相吻合。YANO等的算法溶血预测值偏高，改进模型的计算值较优。

4) 建立了实验指标IH与溶血预测值之间的数学联系，为评估溶血模型提供了理论方法。

[1] 韩伟, 韩冰雪, 王汉义, 等. 基于CFD螺旋离心式血泵与离心式血泵内部流场的数值分析[J]. 兰州理工大学学报, 2014, 40(5): 56−59. HAN Wei, HAN Bingxue, WANG Hanyi, et al. Number analysis of internal flow field in screw centrifugal blood pump and centrifugal blood pump based on CFD[J]. Journal of Lanzhou University of Technology, 2014, 40(5): 56−59.

[2] FRASER K H, TASKIN M E, GRIFFITH B P, et al. The use of computational fluid dynamics in the development of ventricular assist devices[J]. Medical Engineering & Physics, 2011, 33(3): 263−280.

[3] COWGER J A, ROMANO M A, SHAH P, et al. Hemolytic:a harbinger of adverse outcome after left ventricular assist device implant[J]. Heart Lung Transplant, 2014, 33(1): 35−43.

[4] TASKIN M E, FRASER K H, ZHANG T, et al. Computational characterization of flow and hemolytic performance of the UltraMag blood pump for circulatory support[J]. Artificial Organs, 2010, 34(12): 1099−1113.

[5] LI Tieyan, YE Liang, FW Hong, et al. The simulation of multiphase flow field in implantable blood pump and analysis of hemolytic capability[J]. Journal of Hydrodynamics: Ser B, 2013, 25(4): 606−615.

[6] GOUBERGRITS L. Numerical modeling of blood damage: current status, challenges and future prospects[J]. Expert Review of Medical Devices, 2006, 3(5): 527−531.

[7] YANO T, SEKINE K, MITOH A, et al. An estimation method of hemolysis within an axial flow blood pump by computational fluid dynamics analysis[J]. Artificial Organs, 2003, 27(10): 920−925.

[8] GARON A, FARINAS M I. Fast three-dimensional numerical hemolysis approximation[J]. Artificial Organs, 2004, 28(11): 1016−1025.

[9] TASKIN M E, FRASER K H, ZHANG T, et al. Evaluation of eulerian and lagrangian models for hemolysis estimation[J]. ASAIO Journal, 2012, 58(4): 363−372.

[10] 周冰晶, 荆腾, 王芳群, 等. 两级轴流血泵基于血液损伤的数值分析[J]. 生物医学工程学杂志, 2016, 33(4): 686−690. ZHOU Bingjing, JING Teng, WANG Fangqun, et al. Numerical analysis of two-stage axial blood pump based on blood damage[J]. Journal of Biomedical Engineering, 2013, 25(4): 606−615.

[11] 吴华春, 龚高, 王子彦, 等. 轴流式磁悬浮血泵流场数值模拟及溶血预测[J]. 中国机械工程, 2013, 24(3): 399−403. WU Huachun, GONG Gao, WANG Ziyan, et al. Flow field numerical simulation and hemolytic for axial flow maglev blood pump[J]. China Mechanical Engineering, 2013, 24(3): 339−403.

[12] 寿宸, 郭勇君, 苏磊, 等. 基于快速溶血预估模型的离心血泵叶轮特性数值分析[J]. 生物医学工程学杂志, 2014, 31(6): 1260−1264. SHOU Chen, GUO Yongjun, SU Lei, et al. Numerical assessment of impeller features of centrifugal blood pump based on fast hemolysis approximation model[J]. Journal of Biomedical Engineering, 2014, 31(6): 1260−1264.

[13] 谭卓, 谭建平, 刘云龙, 等. 大间隙磁力驱动轴流式血泵的电磁特性[J]. 中南大学学报(自然科学版), 2015, 46(1): 99−106. TAN Zhuo, TAN Jianping, LIU Yunlong, et al. Electromagnetic characteristics of large gap magnetic driving axial flow blood pump[J]. Journal of Central South University (Science and Technology), 2015, 46(1): 99−106.

[14] 云忠, 向闯, 蔡超, 等. 边界振动流场对单个红细胞损伤影响分析[J]. 生物医学工程学杂志, 2016, 33(1): 78−82. YUN Zhong, XIANG Chuang, CAI Chao, et al. Analysis of influence on single erythrocyte injury caused by oscillating boundary flow field[J]. Journal of Biomedical Engineering, 2016, 33(1): 78−82.

[15] 云忠, 谭建平. 基于血液撞击损伤机理的高速螺旋血泵仿真分析[J]. 中南大学学报(自然科学版), 2008, 39(1): 135−142. YUN Zhong, TAN Jianping. Simulation analysis of high-speed spiral blood pump based on impacting injure principle of blood[J]. Journal of Central South University (Science and Technology), 2015, 46(1): 99−106.

[16] GIERSIEPEN M, WURZINGER L, OPITZ R, et al. Estimation of shear stress-related blood damage in heart valve prostheses: in vitro comparison of 25 aortic valves[J]. The International Journal of Artificial Organs, 1990, 13(5): 300−306.

[17] 吴广辉, 蔺嫦燕, 张锡文, 等. 磁驱动血泵溶血分析[J]. 中国生物医学工程学报, 2010, 29(3): 473−476. WU Guanghui, LIN Changyan, ZHANG Xiwen, et al. Hemolysis test of an axial flow ventricular assistant device[J]. Chinese Journal of Biomedical Engineering, 2010, 29(3): 473−476.

(编辑 陈灿华)

Flow field analysis and hemolytic prediction of axial blood pump based on multiphase flow

WANG Dailing, TAN Jianping, YU Zheqin

(School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

In order to study the distribution of blood cells in blood pump and the method of hemolytic prediction, the self-made axial flow blood pump was taken as an example, analytical method of multiphase flow and multiple reference frame method (MRF) technology were used, numerical analytical model was established. The validity of the model was verified by cardiopulmonary bypass. The internal distribution of blood cell concentration, velocity, pressure and so on in blood pump was analyzed. In order to get the blood cell damage area and the general law, the improved particle tracking method was used to evaluate the hemolytic performance of blood pump, and the conversion relationship between the standard hemolytic index (NIH) and hemolytic prediction value was obtained. The results show that the blood cells in the flow channel are not evenly distributed, and there is separation phenomenon at the impeller blood pump. When the internal stress in the area is below 200 Pa, volume fraction is about 98.6%, high shear stress is mainly located in the gap between the impeller’s top and the outer shell. Under the condition that shear stress is a constant, the improved hemolytic prediction model can match the hemolytic formula obtained by Giersiepen test well. The modified hemolytic model is used to estimate the hemolysis value of the blood pump and the average hemolytic value is 0.005 7, which shows that the modified hemolytic model has good hemolytic capability.

blood pump; multiphase flow; standard hemolytic index; hemolytic model

TH312

A

1672−7207(2018)08−1929−07

10.11817/j.issn.1672−7207.2018.08.013

2017−08−10；

2017−10−21

国家自然科学基金资助项目(51475477，3167099)(Projects(51475477, 3167099) supported by the National Natural Science Foundation of China)

谭建平，博士，教授，从事电液控制及血泵研究；E-mail：jptan@163.com