随机梁式结构静力损伤识别的一种改进方法

， ， ，

(1.武汉理工大学 土木工程与建筑学院,武汉 430070；2.南昌工学院 建筑工程学院,南昌 330108)

1 引 言

土木工程结构的健康监测是土木工程学科发展前沿的一个重要方向[1,2]，而结构损伤的识别研究是结构健康监测研究的一个关键内容。各种损伤识别法已经得到了广泛的研究[3]。静力损伤识别方法可以较为方便地测量到结构的变形或应变，因此，静力损伤识别方法是一种值得研究和发展的损伤识别方法。

国内外学者对静力损伤识别方法做了许多研究。刘毅等[4]通过建立ARMA模型计算了损伤前后两状态模型的残差和方差，提出以残差方差之比作为损伤敏感特征，并建立了基于F分布的假设检验来辨识结构的状态。Kouchmeshky等[5]利用较少的静力测试数据，通过一个新的协同进化算法交互式搜索找到了结构可能发生损坏的单元。Buda等[6]提出了静力作用下欧拉伯努利梁损伤识别的非均匀优化程序，利用分析模型响应与测试数据之间的误差函数识别损伤，并探讨了测量误差对识别参数的影响。张宇鑫等[7]基于静力位移测试数据，构建结构柔度矩阵，提出了静力位移DLV方法。Seyedpoor等[8]通过建立损伤前后的静态应变能指标来确定损伤位置，该方法在考虑测量误差的前提下，仍能准确定位损伤位置，但未提及损伤程度的确定方法。陈孝珍等[9]首次提出了灰色曲率关联系数的概念，并将其应用到结构的静力损伤识别中，通过静态位移曲率置信因子的大小评估单元损伤状态，进而利用最小二乘法确定损伤程度。Impollonia等[10]使用节点位移和速度的静态二阶矩的近似参数解给出了基于统计矩的损伤识别方法，该方法从确定性的角度出发，实现了利用静力测量数据识别结构损伤。测量误差和结构系统本身及其有限元模型近似等随机性对实际工程中的损伤识别结果具有很大影响，甚至会掩盖真实的损伤情况。基于概率统计分析的结构损伤识别方法能够很好地考虑一些不确定因素的影响，有望成为解决工程结构损伤识别问题的一般方法。张清华等[11]利用摄动法和蒙特卡洛法研究了测量误差对损伤识别结果的影响规律，在基于概率统计理论的基础上提出了利用概率评估损伤方法，但未考虑模型误差对识别结果的影响。Ebrahimian等[12]提出了运用贝叶斯估计的非线性有限元模型修正方法来识别损伤，并讨论了存在较大测量误差和初始模型误差的情况下损伤识别方法的稳定性。Liu等[13]结合概率论和结构设计理论研究了结构的损伤行为，并利用概率方法提高了损伤识别的有效性。这些方法虽然考虑了静力数据测量误差和初始模型误差的存在，但对初始模型和概率损伤的定义和描述还不够清楚，文献[14]从动力学角度提出了基于统计模型的损伤识别方法。与该方法不同，文献[15]利用静力测量数据，结合静力凝聚和摄动法，提出了一种基于随机有限元模型的梁式结构静力损伤识别方法。

本文基于文献[15]所给出的损伤识别方法提出了一种改进的方法。该方法假定结构在正常服役期内整体退化并不严重，损伤只会发生在局部构件上，即结构系统的大部分构件或位置认为是完好的。基于这个假定，在文献[15]给出的损伤识别方法基础上，通过设定损伤概率指标的阈值和反复迭代，不断缩小损伤的查找范围，并最终确定损伤位置和程度。数值算例和简支梁静力试验均表明，新方法对文献[15]方法中出现的损伤误判情况有明显的改进。

2 基于随机有限元模型的静力损伤识别方法

2.1 随机损伤指数及其求解方程

假定结构损伤是由结构局部单元刚度的折减造成的，利用有限元方法进行结构建模，将结构局部损伤表示为各个单元刚度的折减之和，损伤后的刚度矩阵Kd可以由初始刚度矩阵Ka和刚度矩阵的改变量来表示，即

(1)

式中n为结构单元的总数，αi为结构第i个单元刚度的折减系数，即下文所说的损伤指数，Ki为结构第i个单元刚度矩阵，其维数与整体刚度矩阵相同。

由于在静力测量过程中，传统的测量方法无法测得转动自由度，因此采用静力凝聚法消去刚度矩阵中的转动自由度，凝聚后的损伤刚度矩阵Kd t可用初始刚度矩阵的子矩阵和损伤指数来表示，即

(2)

式中Ka t t,Ka t θ，Ka θ t和Ka θ θ分别为Ka对应于转动和平移自由度的子矩阵，Kd t t，Kd t θ，Kd θ t和Kd θ θ分别为Kd对应于转动和平移自由度的子矩阵，Ki t t，Ki t θ，Ki θ t和Ki θ θ分别为Ki对应于转动和平移自由度的子矩阵[15]。

假定结构损伤前后承受的静力荷载相同，可将损伤前后的静力平衡方程建立等式关系，即

Ka txa t=Kd txd t

(3)

式中Ka t为经过静力凝聚简化后的初始模型刚度，xa t为初始模型的竖向位移向量，xd t为损伤模型的竖向位移向量。

将Kd t进行一阶泰勒展开，可写为

令Kd t|α = 0=Ka t，Kt i=(∂Kd t/∂αi)|α = 0

Δxt=xa t-xd t

则式(3)可转化为

(4)

(5)

2.2 随机控制方程的摄动解

对于随机方程(5)的求解，涉及的随机量变化幅度较大时，可采用递推随机有限元法或蒙特卡洛法。为简便起见，本文介绍低阶摄动法。

利用摄动法将式(5)展开，考虑零阶量ξ0,有

Lsα0=Rs 0

(6)

式中α0=[α10，α20，…，αn 0]T

Rs 0=Ka t 0(xa t 0-xd t)

Ls=[Kt1xd t,Kt 2xd t,…,Kt nxd t]

同理，对于ξl(l=1,…,m)项，由式(5)得

Lsα1=Rs1

(7)

式中α1=[αi l]n × m(i=1,…,n;l=1,…,m)

Rs 1= [Ka t 0xa t 1+Ka t 1(xa t 0-xd t 0)，

Ka t 0xa t 2+Ka t 2(xa t 0-xd t 0)，…，

Ka t 0xa t m+Ka t m(xa t 0-xd t)]

对于ξm + 1项，有

(8)

式中α2=[αi,m + 1]n × 1(i=1,…,n)

利用式(6～8)可依次求解获得αi 0和αi l(i=1,…,n;l=1,…,m+1),从而可得随机结构损伤指数向量α的统计特性。

2.3 损伤的概率定义

本文运用结构安全可靠度分析中失效概率的概念来描述结构单元损伤的概率[15]，即初始的单元刚度系数Ka i大于受损后单元刚度系数Kd i的概率，可表示为

(9)

式中损伤前后的单元刚度系数为标量。

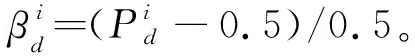
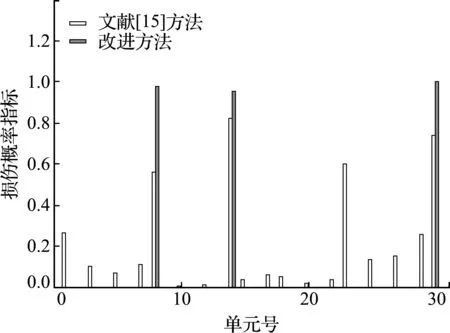
3 基于损伤概率的改进方法

为了进一步提高梁式结构损伤识别结果的准确性和稳定性，本文利用损伤概率指标的定义，在第2节静力损伤识别方法的基础上发展了一种改进方法。该方法假定结构损伤只是局部的，而不是大量发生或是整体退化。

首先利用式(6～8)求出αi 0和αi l(i=1,…,n;l=1,…,m+1),再根据α的统计特性计算各单元损伤概率指标，通过设定概率损伤阈值对损伤进行判断。具体而言，如果单元j的损伤概率指标满足式(10)，

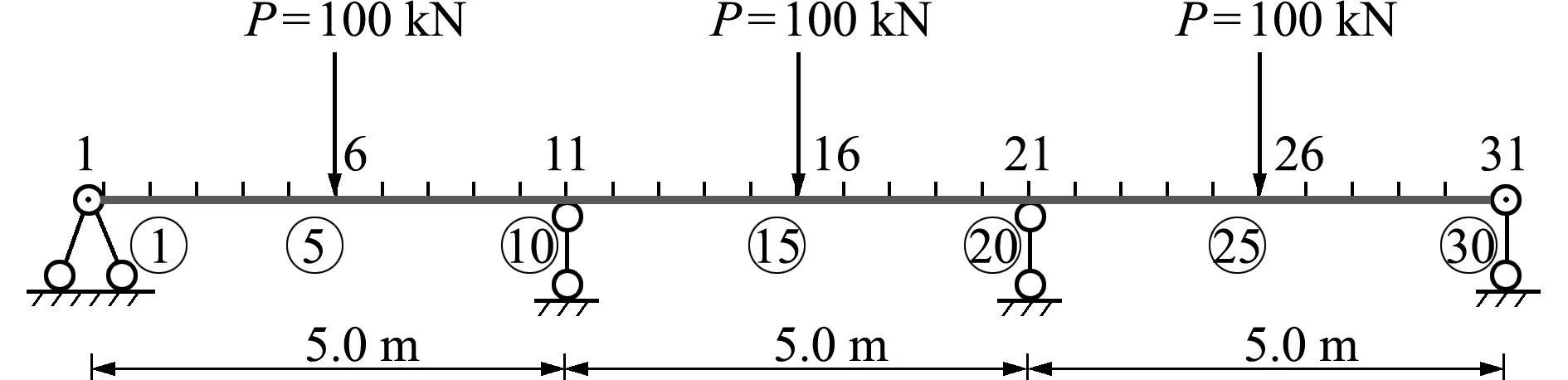
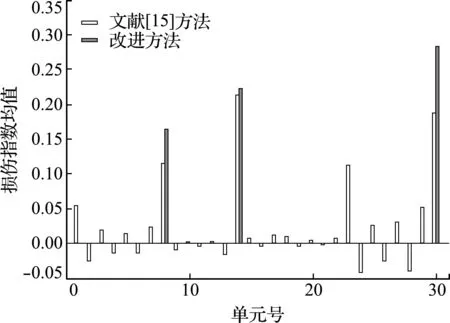
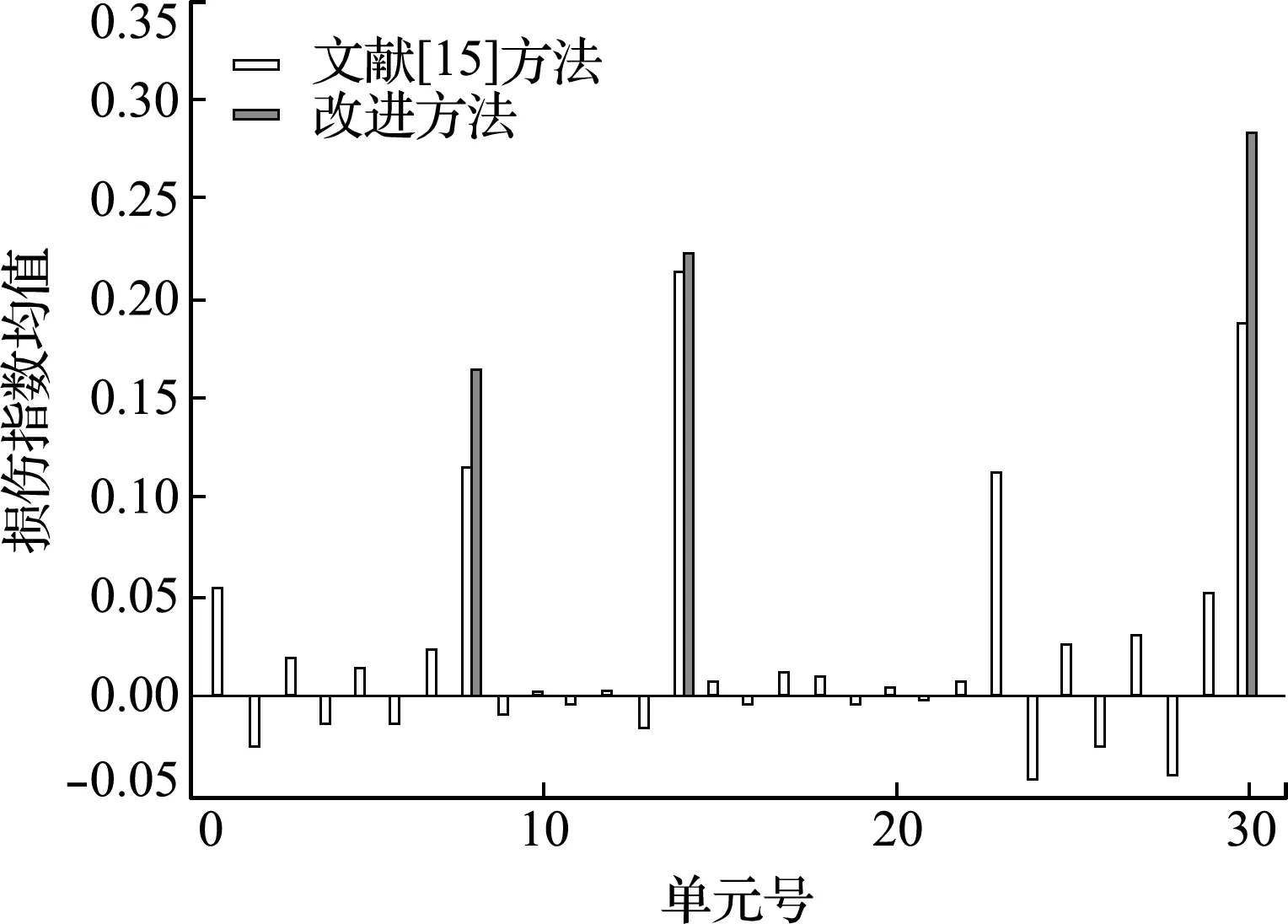
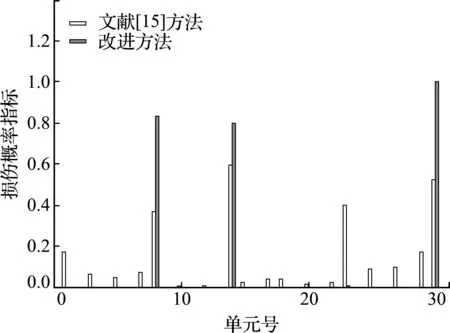
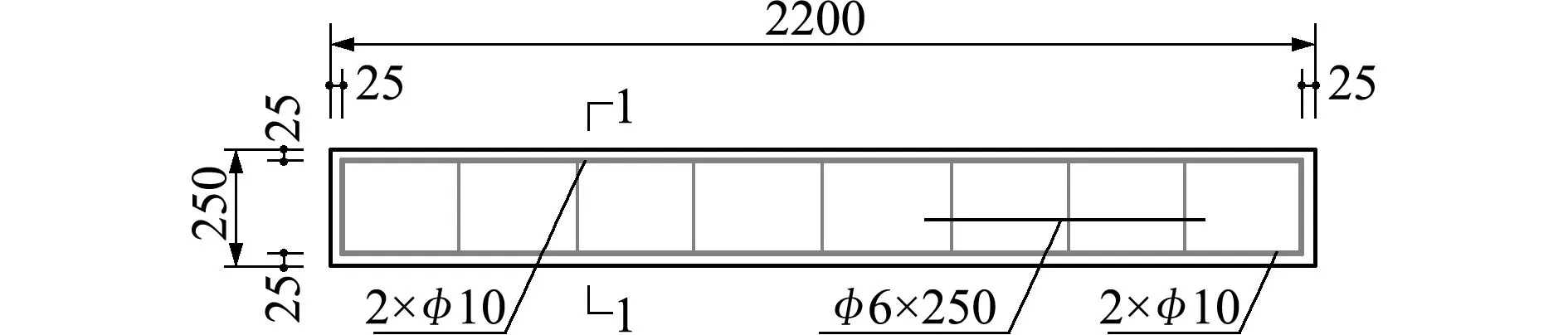
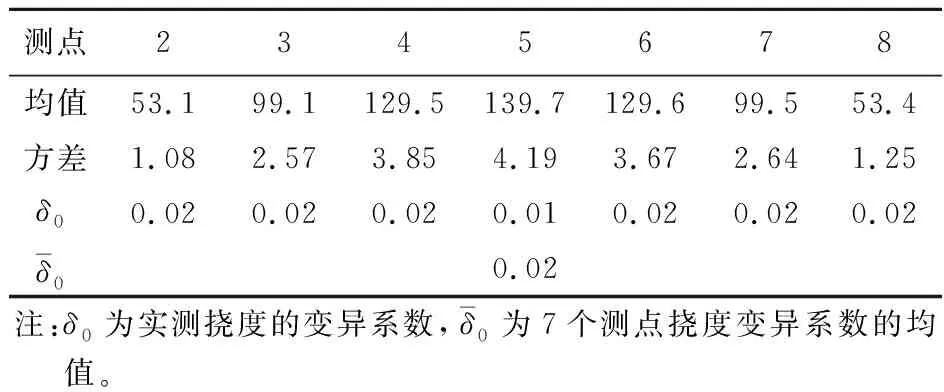
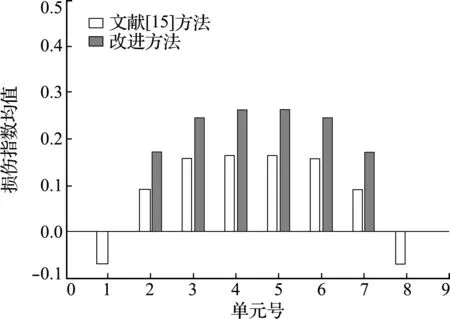
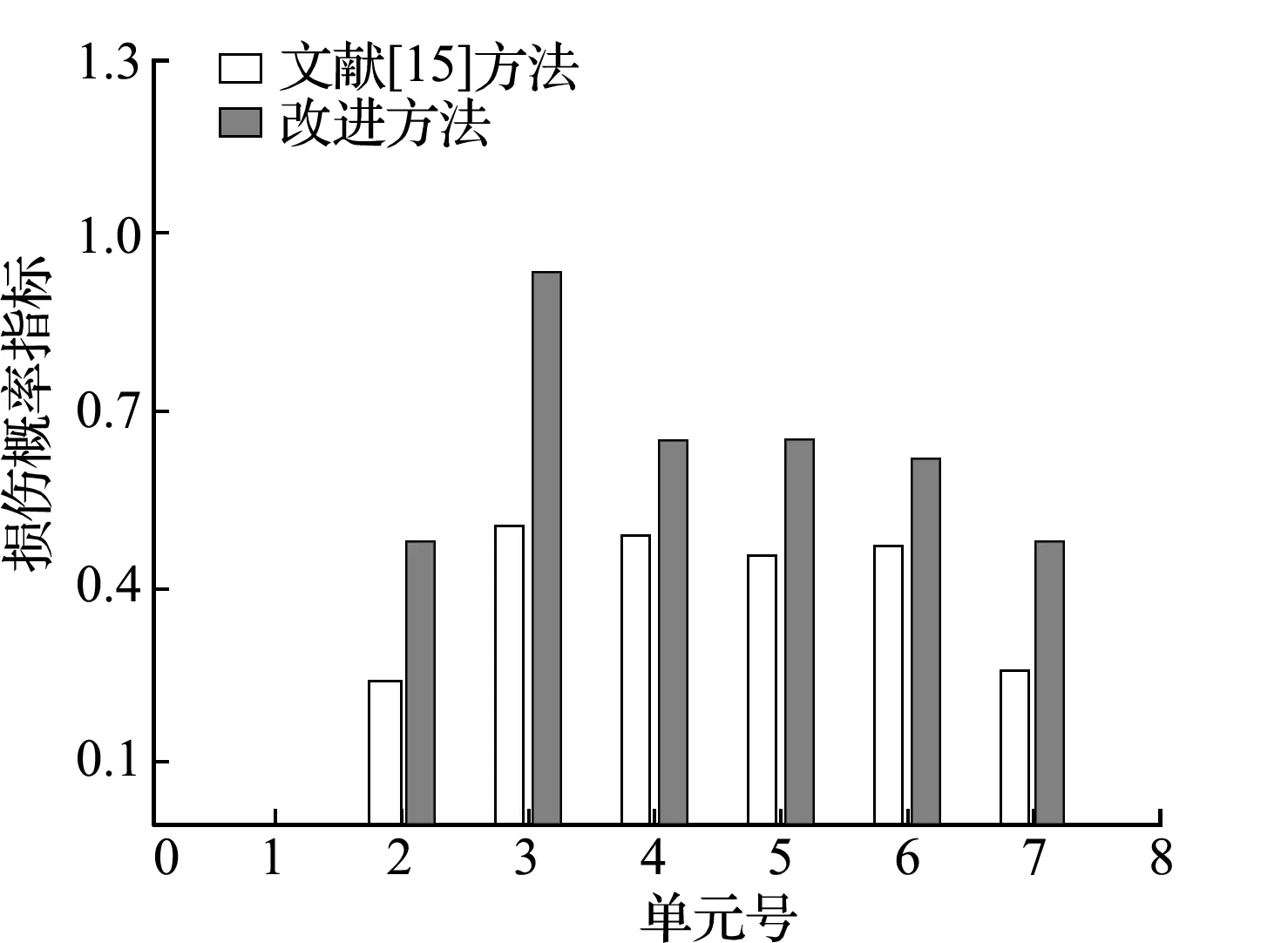
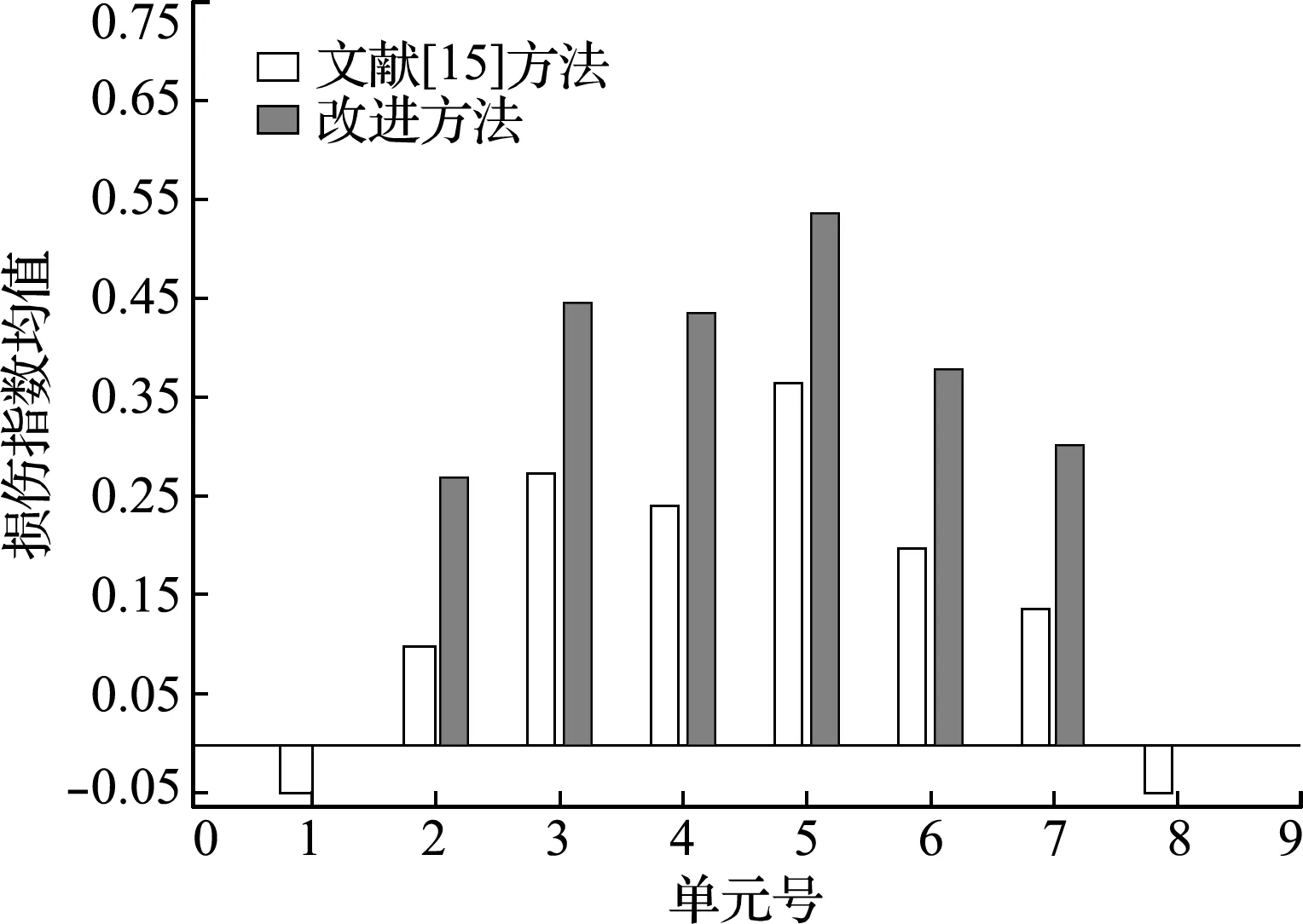
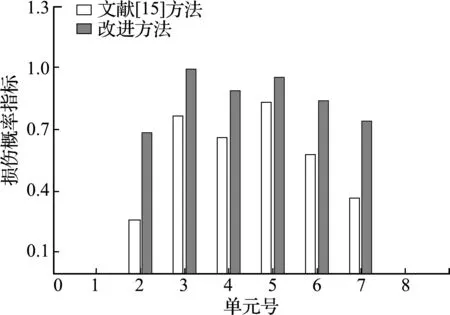
βjd

(10)

式中Pd为设定的概率阈值，根据经验可取为0.2。把损伤概率指标小于概率阈值的单元确定为无损伤单元，对于其他待识别的单元，重新假定损伤指数为随机量ξ的函数，并回代到随机控制方程中进行求解。详细计算步骤如下。

设损伤概率指标满足式(10)的单元个数为n1,以n1=2为例，假设其单元号分别为i和j，并将对应的损伤指数向量中的元素设定为0。然后重新调整α0中各元素顺序，得到新的损伤指数向量零阶展开，可写为

α0=[α0 t,0，0]T

(11)

式中α0t= [α10，α20，…，αi -1,0，αi +1,0，…，αj -1,0，

αj +1,0，…，αn 0]

同时调整Ls,取Ls t为Ls中待识别单元对应的列向量组成的矩阵，可表示为

Ls t= [Kt 1xd t，Kt 2xd t，…，Kt,i -1xd t，Kt,i +1xd t，…，

Kt,j -1xd t，Kt,j +1xd t，Kt nxd t]

(12)

式(6)可重写为

Ls tα0 t=Rs 0

(13)

式中Rs 0意义同式(6)。利用式(13)可求得待识别损伤单元的损伤指数零阶展开向量α0 t。

同理可求得损伤指数一阶展开矩阵，对于ξl(l=1,…,m)项，调整矩阵α1=[αi l]n × m中已确定的无损单元对应的行向量元素为0，令矩阵α1t为矩阵α1中待识别单元对应的行向量元素组成的矩阵，即

α1t= [α1l，α2l，…，α(i -1)l，α(i +1)l，…，α(j -1)l，

α(j +1)l，…，αn l](n -n1)×m

(14)

根据式(7)可有

Ls tα1 t=Rs1

(15)

式中Rs 1的意义同式(7)。利用式(15)可求得ξl(l=1,…,m)对应的待识别单元损伤指数一阶展开矩阵α1 t。

对于ξm +1项，同样地根据上述步骤确定向量α2=[αi,m +1]n × 1中无损单元对应的元素为0，令α2t为α2中非0未知元素组成的向量，即

α2t= [α1,m +1，α2,m +1，…，αi -1,m +1，αi +1,m +1，…，

αj -1,m +1，αj +1,m +1，…，αn,m +1]T

(16)

同时调整L*s,将L*s t写为

(17)

利用式(8)，得到待识别单元对应ξm +1项的损伤指数一阶展开矩阵α2t的求解方程为

Ls tα2t+L*s tα0t=Rs 2

(18)

式中，Rs 2的定义和式(8)一样。

通过对随机控制方程(13，15，18)的求解，可得到新的结构损伤指数，从而得到第一次改进后的损伤识别结果，再重复上述步骤得到第二次改进后的识别结果。反复利用上一次改进的损伤概率指标进行判定和迭代计算，直至结果收敛(一般情况下迭代一到两次即可达到较好的识别效果)。利用最终求得的单元损伤指数均值评估对应结构单元损伤的大小，利用获得的单元损伤概率指标来评估对应结构单元损伤发生的概率。

4 数值算例

如图1所示的三跨连续梁结构模型，其几何参数和材料参数分别取为，梁总长l=15.0 m，各跨长度均为l0=5.0 m，材料的弹性模量E=28 GPa,矩形截面尺寸为b×h=0.3 m×0.8 m，转动惯性矩I=0.0128 m4。将该连续梁结构均匀划分为30个等长的梁单元，同样假定弹性模量的不确定性导致连续梁初始模型的随机性，并假设连续梁每跨的弹性模量为一个独立随机变量，且服从正态分布。在连续梁每一跨的跨中位置施加竖向静力荷载P=100 kN，并假设只测量连续梁各单元节点的竖向位移值。

假定单元8，14和30的弹性模量分别降低15%，20%和25%，同时考虑结构初始模型的不确定性和测量误差对损伤识别结果的影响，假定静力测试数据的变异系数为0.06，根据假定初始模型单元弹性模量的变异系数δ的取值不同，设置两种工况。工况1，当δ=0.15时，损伤识别结果如图2和图3所示；工况2，当δ=0.25时，损伤识别结果如图4和图5所示。

图2～图5的损伤识别结果表明，改进方法的识别结果能更准确地反映连续梁结构的损伤状态。可以看出，对于2个工况，在文献[15]方法的识别结果中，单元1，23和29出现了明显的误判，其中单元23损伤均值误判超过10%，对应的损伤概率指标也达到了0.6。与文献[15]方法的识别结果相比，改进后的方法很好地排除了干扰，而且得到的损伤单元的损伤指数均值更接近算例的假定损伤量，与损伤单元相对应的损伤概率指标也有所提高；从损伤指数均值的结果看，改进方法的识别结果均略大于给定值。这是由于在改进算法中，将损伤概率指标低于设定阈值的单元定为无损单元后，进行再一次的迭代计算时可能会稍微 放大真实损伤单元的损伤程度。另外，静力凝聚也会对结果有一定影响。虽然所施加荷载在各跨的跨中，经研究和比较发现，荷载大小和位置对本文方法的识别效果影响不大，但荷载大小和位置对识别的灵敏度有影响[16]。

图1 随机连续梁结构模型

Fig.1 Model of the continuous beam

图2 随机连续梁工况1下损伤指数均值

Fig.2 Mean values of damage indexes for random continuous beam in case 1

图3 随机连续梁工况1下损伤概率指标

Fig.3 Damage probability indexes of random continuous beam in case 1

5 简支梁损伤识别试验

对一混凝土简支梁做静力加载试验，如图6所示。该简支梁总长度为2.20 m，计算跨度为1.90 m，梁截面尺寸为b×h=0.15 m×0.25 m。浇筑混凝土强度等级为C25，简支梁配筋情况如图7所示。根据试验中制作的混凝土立方体试块的强度测试，确定混凝土的弹性模量E=2.80×104MPa,混凝土弹性模量的变异系数δ=0.24。抗弯试验中利用千斤顶和压力传感器通过分配梁进行加载，用百分表测量梁各点的竖向挠度。相应的计算模型如图8所示，该模型将简支梁划分为8个单元和9个节点。

图4 随机连续梁工况2下损伤指数均值

Fig.4 Mean values of damage indexes for random continuous beam in case 2

图5 随机连续梁工况2下损伤概率指标

Fig.5 Damage probability indexes of random continuous beam in case 2

当荷载P=15 kN时，梁底部各节点实测挠度的统计值列入表1。用本文方法可以得到损伤指数均值及损伤概率指标的识别结果，如图9和图10所示。

图9和图10的识别结果表明，当荷载达到P=15 kN时，梁的弯曲刚度开始降低，纯弯段开始出现损伤，而剪切段的损伤指数和损伤概率指标均较低，还没有完全进入损伤状态。根据《混凝土设计规范》GB 50010—2010计算得到简支梁开裂荷载为11.70 kN，极限承载力(受拉钢筋屈服)为35.28 kN。当荷载低于开裂荷载时，简支梁处于完好状态，本文利用此状态下的节点位移对初始刚度矩阵做了适当的修正。当采用初始模型识别荷载较低的工况时，识别出的损伤指数均值和损伤概率指标均很小，可以认为此时混凝土梁处于无损状态；当荷载稍大于开裂荷载时，简支梁处于截面受弯第二阶段的初期，裂缝不明显，从外观上不容易发现裂缝，但此时梁抗弯刚度开始下降，本文方法能较准确地识别出该阶段梁的损伤。图10中3单元的损伤概率指标大于其他单元，认为是由位移测试误差以及初始模型误差所引起。

图6 混凝土简支梁的受弯试验

Fig.6 Bending test of the simply supported concrete beam

图7 简支梁配筋(单位：mm)

Fig.7 Reinforcement diagram of simply supported beam (unit：mm)

图8 试验混凝土简支梁的力学模型

Fig.8 Mechanical model of the tested simply supported concrete beam

当荷载增加到P=30 kN时，梁底部各节点实测挠度的统计值列入表2。同样的，可以得到损伤指数均值及损伤概率指标的识别结果，如图11和图12所示。

表2 工况2实测位移统计值(单位：0.01 mm)

Tab.2 Statistics of measured displacements in the case 2(unit：0.01 mm)

测点2345678均值53.199.1129.5139.7129.699.553.4方差1.082.573.854.193.672.641.25δ00.020.020.020.010.020.020.02δ-00.02注:δ0为实测挠度的变异系数,δ-0为7个测点挠度变异系数的均值。

图9 混凝土简支梁工况1下损伤指数均值

Fig.9 Mean values of damage indexes for the simply supported concrete beam in case 1

图10 混凝土简支梁工况1下损伤概率指标

Fig.10 Damage probability indexes of the simply supported concrete beam in case 1

图11和图12的识别结果表明,当荷载达到30 kN时，从损伤指数均值看，2～7单元出现不同程度的损伤，本文改进方法的识别结果均大于原有方法结果。如果采用文献[15]方法，很难判断出加载点外的2单元和7单元已进入损伤状态。在此荷载作用下裂缝发展情况如图13所示。可以看出，简支梁纯弯段和剪切段底部出现明显裂缝，梁抗弯刚度明显降低，试验观察结果与识别结果吻合较好。因此，与文献[15]方法相比，本文改进方法的识别结果与真实损伤单元的损伤状态更为吻合，能较好地识别混凝土梁损伤状态，有效地降低损伤误判程度。虽然随着损伤程度的增加，损伤指数均值和损伤概率指标也随之增加，但其趋势不呈线性增长。为了进一步验证识别结果的有效性，后续工作将结合动力测试数据(如频率等)对简支梁的损伤状态做评估和验证。

图11 混凝土简支梁工况2下损伤指数均值

Fig.11 Mean values of damage indexes for the simply supported concrete beam in case 2

图12 混凝土简支梁工况2下损伤概率指标

Fig.12 Damage probability indexes of the simply supported concrete beam in case 2

图13 混凝土梁工况2下的裂缝示意图

Fig.13 Crack diagram of the concrete beam in the case 2

6 结 论

在已有基于静力测试数据的损伤识别方法基础上，提出了一种改进的静力损伤识别方法。这种改进的损伤识别方法同样考虑了梁式结构的初始模型误差和测量误差对损伤识别结果的影响。相较于已有方法，改进方法通过设定损伤概率指标的阈值和反复迭代计算对结构损伤识别进行了改进。简支梁和连续梁结构的数值算例及简支梁静力试验识别结果均表明，该方法可以很好地排除损伤误判单元，提高了结构损伤识别的准确度。在一定的误差范围内，改进方法的损伤识别结果仍能保持较好的准确性，但初始模型不确定性程度的增加会降低判断损伤存在的概率。进一步，采用混凝土简支梁受弯损伤试验，验证了本文方法的有效性。